Big Data Analytics - Kurzanleitung
Das Datenvolumen, mit dem man sich befassen muss, ist in den letzten zehn Jahren auf ein unvorstellbares Niveau explodiert, und gleichzeitig ist der Preis für die Datenspeicherung systematisch gesunken. Private Unternehmen und Forschungseinrichtungen erfassen Terabyte an Daten über die Interaktionen ihrer Benutzer, Unternehmen, soziale Medien sowie Sensoren von Geräten wie Mobiltelefonen und Automobilen. Die Herausforderung dieser Ära besteht darin, dieses Datenmeer zu verstehen. Das ist wobig data analytics kommt ins Bild.
Bei Big Data Analytics werden Daten aus verschiedenen Quellen gesammelt, so gemischt, dass sie für Analysten verfügbar sind, und schließlich Datenprodukte bereitgestellt, die für das Unternehmen nützlich sind.

Der Prozess der Konvertierung großer Mengen unstrukturierter Rohdaten, die aus verschiedenen Quellen abgerufen werden, in ein Datenprodukt, das für Unternehmen nützlich ist, bildet den Kern von Big Data Analytics.
Traditioneller Data Mining-Lebenszyklus
Um einen Rahmen für die Organisation der von einer Organisation benötigten Arbeit und klare Erkenntnisse aus Big Data bereitzustellen, ist es hilfreich, sich diesen als einen Zyklus mit verschiedenen Phasen vorzustellen. Es ist keineswegs linear, dh alle Stufen sind miteinander verbunden. Dieser Zyklus weist oberflächliche Ähnlichkeiten mit dem traditionelleren Data Mining-Zyklus auf, wie in beschriebenCRISP methodology.
CRISP-DM-Methodik
Das CRISP-DM methodologyDies steht für den branchenübergreifenden Standardprozess für Data Mining. In diesem Zyklus werden häufig verwendete Ansätze beschrieben, mit denen Data Mining-Experten Probleme im traditionellen BI-Data Mining angehen. Es wird immer noch in traditionellen BI-Data-Mining-Teams verwendet.
Schauen Sie sich die folgende Abbildung an. Es zeigt die Hauptphasen des Zyklus, wie sie in der CRISP-DM-Methodik beschrieben sind, und wie sie miteinander zusammenhängen.
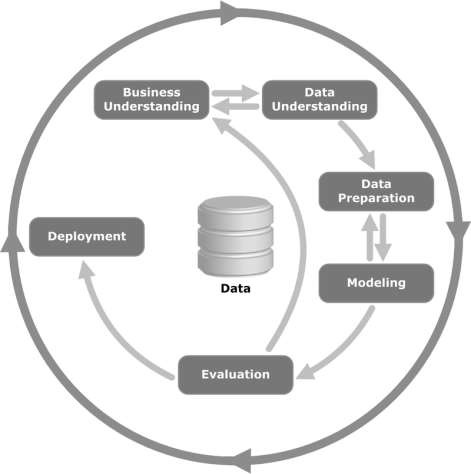
CRISP-DM wurde 1996 konzipiert und im nächsten Jahr als EU-Projekt im Rahmen der ESPRIT-Förderinitiative gestartet. Das Projekt wurde von fünf Unternehmen geleitet: SPSS, Teradata, Daimler AG, NCR Corporation und OHRA (eine Versicherungsgesellschaft). Das Projekt wurde schließlich in SPSS aufgenommen. Die Methodik ist äußerst detailliert und orientiert sich daran, wie ein Data Mining-Projekt spezifiziert werden sollte.
Lassen Sie uns nun etwas mehr über die einzelnen Phasen des CRISP-DM-Lebenszyklus erfahren -
Business Understanding- Diese erste Phase konzentriert sich darauf, die Projektziele und -anforderungen aus geschäftlicher Sicht zu verstehen und dieses Wissen dann in eine Data-Mining-Problemdefinition umzuwandeln. Ein vorläufiger Plan soll die Ziele erreichen. Es kann ein Entscheidungsmodell verwendet werden, insbesondere eines, das unter Verwendung des Entscheidungsmodell- und Notationsstandards erstellt wurde.
Data Understanding - Die Datenverständnisphase beginnt mit einer ersten Datenerfassung und setzt Aktivitäten fort, um sich mit den Daten vertraut zu machen, Datenqualitätsprobleme zu identifizieren, erste Einblicke in die Daten zu gewinnen oder interessante Teilmengen zu erkennen, um Hypothesen für versteckte Informationen zu bilden.
Data Preparation- Die Datenaufbereitungsphase umfasst alle Aktivitäten zum Erstellen des endgültigen Datensatzes (Daten, die in die Modellierungswerkzeuge eingespeist werden) aus den anfänglichen Rohdaten. Datenaufbereitungsaufgaben werden wahrscheinlich mehrmals und nicht in einer vorgeschriebenen Reihenfolge ausgeführt. Zu den Aufgaben gehören die Auswahl von Tabellen, Datensätzen und Attributen sowie die Transformation und Bereinigung von Daten für Modellierungswerkzeuge.
Modeling- In dieser Phase werden verschiedene Modellierungstechniken ausgewählt und angewendet und ihre Parameter auf optimale Werte kalibriert. In der Regel gibt es mehrere Techniken für denselben Data Mining-Problemtyp. Einige Techniken haben spezielle Anforderungen an die Datenform. Daher ist es häufig erforderlich, zur Datenaufbereitungsphase zurückzukehren.
Evaluation- In dieser Phase des Projekts haben Sie ein Modell (oder Modelle) erstellt, das aus Sicht der Datenanalyse eine hohe Qualität zu haben scheint. Bevor Sie mit der endgültigen Bereitstellung des Modells fortfahren, ist es wichtig, das Modell gründlich zu bewerten und die zur Erstellung des Modells ausgeführten Schritte zu überprüfen, um sicherzustellen, dass die Geschäftsziele ordnungsgemäß erreicht werden.
Ein wichtiges Ziel ist es festzustellen, ob es ein wichtiges Geschäftsproblem gibt, das nicht ausreichend berücksichtigt wurde. Am Ende dieser Phase sollte eine Entscheidung über die Verwendung der Data Mining-Ergebnisse getroffen werden.
Deployment- Die Erstellung des Modells ist in der Regel nicht das Ende des Projekts. Selbst wenn der Zweck des Modells darin besteht, das Wissen über die Daten zu verbessern, muss das gewonnene Wissen so organisiert und präsentiert werden, dass es für den Kunden nützlich ist.
Abhängig von den Anforderungen kann die Bereitstellungsphase so einfach wie das Erstellen eines Berichts oder so komplex wie das Implementieren einer wiederholbaren Datenbewertung (z. B. Segmentzuweisung) oder eines Data Mining-Prozesses sein.
In vielen Fällen ist es der Kunde, nicht der Datenanalyst, der die Bereitstellungsschritte ausführt. Selbst wenn der Analyst das Modell bereitstellt, ist es für den Kunden wichtig, im Voraus zu verstehen, welche Aktionen ausgeführt werden müssen, um die erstellten Modelle tatsächlich nutzen zu können.
SEMMA-Methodik
SEMMA ist eine weitere von SAS entwickelte Methode zur Modellierung von Data Mining. Es steht fürSreichlich, Explore, Modifizieren, Model und Asses. Hier ist eine kurze Beschreibung seiner Stadien -
Sample- Der Prozess beginnt mit der Datenerfassung, z. B. der Auswahl des zu modellierenden Datensatzes. Der Datensatz sollte groß genug sein, um genügend Informationen zum Abrufen zu enthalten, aber klein genug, um effizient verwendet zu werden. Diese Phase befasst sich auch mit der Datenpartitionierung.
Explore - Diese Phase umfasst das Verständnis der Daten, indem mithilfe der Datenvisualisierung erwartete und unerwartete Beziehungen zwischen den Variablen sowie Anomalien ermittelt werden.
Modify - Die Änderungsphase enthält Methoden zum Auswählen, Erstellen und Transformieren von Variablen zur Vorbereitung der Datenmodellierung.
Model - In der Modellphase liegt der Schwerpunkt auf der Anwendung verschiedener Modellierungstechniken (Data Mining) auf die vorbereiteten Variablen, um Modelle zu erstellen, die möglicherweise das gewünschte Ergebnis liefern.
Assess - Die Auswertung der Modellierungsergebnisse zeigt die Zuverlässigkeit und Nützlichkeit der erstellten Modelle.
Der Hauptunterschied zwischen CRISM-DM und SEMMA besteht darin, dass sich SEMMA auf den Modellierungsaspekt konzentriert, während CRISP-DM Phasen des Zyklus vor der Modellierung eine größere Bedeutung beimisst, z. B. das Verstehen des zu lösenden Geschäftsproblems, das Verstehen und die Vorverarbeitung der zu verarbeitenden Daten Als Eingabe werden beispielsweise Algorithmen für maschinelles Lernen verwendet.
Big Data-Lebenszyklus
Im heutigen Big-Data-Kontext sind die bisherigen Ansätze entweder unvollständig oder suboptimal. Beispielsweise ignoriert die SEMMA-Methodik die Datenerfassung und Vorverarbeitung verschiedener Datenquellen vollständig. Diese Phasen machen normalerweise den größten Teil der Arbeit in einem erfolgreichen Big-Data-Projekt aus.
Ein Big-Data-Analysezyklus kann in der folgenden Phase beschrieben werden:
- Geschäftsproblemdefinition
- Research
- Personalbewertung
- Datenerfassung
- Daten Munging
- Datenspeicher
- Explorative Datenanalyse
- Datenvorbereitung für Modellierung und Bewertung
- Modeling
- Implementation
In diesem Abschnitt werden wir uns mit jeder dieser Phasen des Big-Data-Lebenszyklus befassen.
Geschäftsproblemdefinition
Dies ist ein Punkt, der im traditionellen Lebenszyklus von BI- und Big-Data-Analysen häufig vorkommt. Normalerweise ist es eine nicht triviale Phase eines Big-Data-Projekts, das Problem zu definieren und richtig zu bewerten, wie viel potenziellen Gewinn es für ein Unternehmen haben kann. Es liegt auf der Hand, dies zu erwähnen, aber es muss bewertet werden, welche Gewinne und Kosten das Projekt erwartet.
Forschung
Analysieren Sie, was andere Unternehmen in derselben Situation getan haben. Dies beinhaltet die Suche nach Lösungen, die für Ihr Unternehmen angemessen sind, obwohl andere Lösungen an die Ressourcen und Anforderungen Ihres Unternehmens angepasst werden müssen. In dieser Phase sollte eine Methodik für die zukünftigen Phasen definiert werden.
Personalbewertung
Sobald das Problem definiert ist, ist es sinnvoll, weiter zu analysieren, ob die aktuellen Mitarbeiter das Projekt erfolgreich abschließen können. Herkömmliche BI-Teams sind möglicherweise nicht in der Lage, eine optimale Lösung für alle Phasen zu liefern. Daher sollte vor Beginn des Projekts überlegt werden, ob ein Teil des Projekts ausgelagert oder mehr Mitarbeiter eingestellt werden müssen.
Datenerfassung
Dieser Abschnitt ist der Schlüssel für einen Big-Data-Lebenszyklus. Es definiert, welche Art von Profilen benötigt wird, um das resultierende Datenprodukt zu liefern. Das Sammeln von Daten ist ein nicht trivialer Schritt des Prozesses. Normalerweise werden unstrukturierte Daten aus verschiedenen Quellen gesammelt. Ein Beispiel könnte das Schreiben eines Crawlers sein, um Bewertungen von einer Website abzurufen. Dies beinhaltet den Umgang mit Text, möglicherweise in verschiedenen Sprachen, für deren Fertigstellung normalerweise viel Zeit erforderlich ist.
Daten Munging
Sobald die Daten beispielsweise aus dem Internet abgerufen wurden, müssen sie in einem benutzerfreundlichen Format gespeichert werden. Nehmen wir an, dass die Daten von verschiedenen Standorten abgerufen werden, an denen die Daten jeweils unterschiedlich angezeigt werden.
Angenommen, eine Datenquelle gibt Bewertungen in Bezug auf die Bewertung in Sternen ab, daher ist es möglich, dies als Zuordnung für die Antwortvariable zu lesen y ∈ {1, 2, 3, 4, 5}. Eine andere Datenquelle gibt Überprüfungen mit zwei Pfeilen, eines für die Aufwärtsabstimmung und das andere für die Abwärtsabstimmung. Dies würde eine Antwortvariable des Formulars impliziereny ∈ {positive, negative}.
Um beide Datenquellen zu kombinieren, muss eine Entscheidung getroffen werden, um diese beiden Antwortdarstellungen gleichwertig zu machen. Dies kann das Konvertieren der ersten Datenquellen-Antwortdarstellung in die zweite Form beinhalten, wobei ein Stern als negativ und fünf Sterne als positiv betrachtet werden. Dieser Prozess erfordert oft eine große Zeitzuweisung, um mit guter Qualität geliefert zu werden.
Datenspeicher
Sobald die Daten verarbeitet sind, müssen sie manchmal in einer Datenbank gespeichert werden. Big-Data-Technologien bieten diesbezüglich zahlreiche Alternativen. Die häufigste Alternative ist die Verwendung des Hadoop-Dateisystems für die Speicherung, das Benutzern eine eingeschränkte Version von SQL bietet, die als HIVE Query Language bezeichnet wird. Auf diese Weise können die meisten Analyseaufgaben aus Anwendersicht auf ähnliche Weise ausgeführt werden wie in herkömmlichen BI-Data-Warehouses. Weitere zu berücksichtigende Speicheroptionen sind MongoDB, Redis und SPARK.
Diese Phase des Zyklus hängt mit dem Wissen der Humanressourcen hinsichtlich ihrer Fähigkeit zusammen, verschiedene Architekturen zu implementieren. Modifizierte Versionen traditioneller Data Warehouses werden immer noch in großen Anwendungen verwendet. Beispielsweise bieten Teradata und IBM SQL-Datenbanken an, die Terabyte an Daten verarbeiten können. Open Source-Lösungen wie postgreSQL und MySQL werden immer noch für große Anwendungen verwendet.
Obwohl es Unterschiede in der Funktionsweise der verschiedenen Speicher im Hintergrund gibt, bieten die meisten Lösungen auf Clientseite eine SQL-API. Ein gutes Verständnis von SQL ist daher immer noch eine Schlüsselkompetenz für die Big-Data-Analyse.
Diese Phase a priori scheint das wichtigste Thema zu sein, in der Praxis ist dies nicht der Fall. Es ist nicht einmal eine wesentliche Phase. Es ist möglich, eine Big-Data-Lösung zu implementieren, die mit Echtzeitdaten arbeitet. In diesem Fall müssen wir nur Daten sammeln, um das Modell zu entwickeln, und es dann in Echtzeit implementieren. Es wäre also überhaupt nicht erforderlich, die Daten formal zu speichern.
Explorative Datenanalyse
Sobald die Daten bereinigt und so gespeichert wurden, dass Erkenntnisse daraus abgerufen werden können, ist die Datenexplorationsphase obligatorisch. Das Ziel dieser Phase ist es, die Daten zu verstehen. Dies geschieht normalerweise mit statistischen Techniken und dem Zeichnen der Daten. Dies ist eine gute Phase, um zu bewerten, ob die Problemdefinition sinnvoll oder machbar ist.
Datenvorbereitung für Modellierung und Bewertung
In dieser Phase werden die zuvor abgerufenen bereinigten Daten umgeformt und eine statistische Vorverarbeitung für die Imputation fehlender Werte, die Erkennung von Ausreißern, die Normalisierung, die Merkmalsextraktion und die Merkmalsauswahl verwendet.
Modellieren
In der vorherigen Phase sollten mehrere Datensätze für Training und Test erstellt worden sein, beispielsweise ein Vorhersagemodell. In dieser Phase werden verschiedene Modelle ausprobiert und das Geschäftsproblem gelöst. In der Praxis ist es normalerweise erwünscht, dass das Modell einen Einblick in das Geschäft gibt. Schließlich wird das beste Modell oder die beste Modellkombination ausgewählt, um die Leistung anhand eines ausgelassenen Datensatzes zu bewerten.
Implementierung
In dieser Phase wird das entwickelte Datenprodukt in die Datenpipeline des Unternehmens implementiert. Dazu muss während der Arbeit des Datenprodukts ein Validierungsschema eingerichtet werden, um dessen Leistung zu verfolgen. Im Fall der Implementierung eines Vorhersagemodells würde diese Phase beispielsweise die Anwendung des Modells auf neue Daten umfassen und das Modell bewerten, sobald die Antwort verfügbar ist.
In Bezug auf die Methodik unterscheidet sich die Big-Data-Analyse erheblich vom traditionellen statistischen Ansatz des experimentellen Designs. Analytics beginnt mit Daten. Normalerweise modellieren wir die Daten so, dass eine Antwort erklärt wird. Ziel dieses Ansatzes ist es, das Antwortverhalten vorherzusagen oder zu verstehen, wie sich die Eingabevariablen auf eine Antwort beziehen. Normalerweise wird in statistischen Versuchsplänen ein Experiment entwickelt und als Ergebnis werden Daten abgerufen. Auf diese Weise können Daten auf eine Weise generiert werden, die von einem statistischen Modell verwendet werden kann, bei dem bestimmte Annahmen wie Unabhängigkeit, Normalität und Randomisierung gelten.
In der Big-Data-Analyse werden uns die Daten präsentiert. Wir können kein Experiment entwerfen, das unser bevorzugtes statistisches Modell erfüllt. Bei umfangreichen Analyseanwendungen ist nur zum Bereinigen der Daten ein großer Arbeitsaufwand (normalerweise 80% des Aufwands) erforderlich, sodass er von einem Modell für maschinelles Lernen verwendet werden kann.
Wir haben keine einzigartige Methodik für echte Großanwendungen. Normalerweise ist nach der Definition des Geschäftsproblems eine Forschungsphase erforderlich, um die zu verwendende Methodik zu entwerfen. Es sind jedoch allgemeine Richtlinien relevant, die erwähnt werden müssen und für fast alle Probleme gelten.
Eine der wichtigsten Aufgaben in der Big Data-Analyse ist statistical modelingDies bedeutet überwachte und unbeaufsichtigte Klassifizierungs- oder Regressionsprobleme. Sobald die Daten bereinigt und vorverarbeitet sind und für die Modellierung zur Verfügung stehen, sollte sorgfältig darauf geachtet werden, verschiedene Modelle mit angemessenen Verlustmetriken zu bewerten. Sobald das Modell implementiert ist, sollten weitere Bewertungen und Ergebnisse gemeldet werden. Eine häufige Gefahr bei der prädiktiven Modellierung besteht darin, das Modell nur zu implementieren und niemals seine Leistung zu messen.
Wie im Big-Data-Lebenszyklus erwähnt, sind die Datenprodukte, die sich aus der Entwicklung eines Big-Data-Produkts ergeben, in den meisten Fällen einige der folgenden:
Machine learning implementation - Dies kann ein Klassifizierungsalgorithmus, ein Regressionsmodell oder ein Segmentierungsmodell sein.
Recommender system - Ziel ist es, ein System zu entwickeln, das Entscheidungen basierend auf dem Benutzerverhalten empfiehlt. Netflix ist das charakteristische Beispiel für dieses Datenprodukt, bei dem basierend auf den Bewertungen der Benutzer andere Filme empfohlen werden.
Dashboard- Unternehmen benötigen normalerweise Tools zur Visualisierung aggregierter Daten. Ein Dashboard ist ein grafischer Mechanismus, um diese Daten zugänglich zu machen.
Ad-Hoc analysis - Normalerweise haben Geschäftsbereiche Fragen, Hypothesen oder Mythen, die durch Ad-hoc-Analyse mit Daten beantwortet werden können.
In großen Organisationen ist es für die erfolgreiche Entwicklung eines Big-Data-Projekts erforderlich, dass das Management das Projekt sichert. Dies beinhaltet normalerweise die Suche nach einem Weg, um die geschäftlichen Vorteile des Projekts aufzuzeigen. Wir haben keine eindeutige Lösung für das Problem, Sponsoren für ein Projekt zu finden, aber im Folgenden finden Sie einige Richtlinien:
Überprüfen Sie, wer und wo die Sponsoren anderer Projekte sind, die denen ähneln, die Sie interessieren.
Persönliche Kontakte in Schlüsselpositionen des Managements helfen, sodass jeder Kontakt ausgelöst werden kann, wenn das Projekt vielversprechend ist.
Wer würde von Ihrem Projekt profitieren? Wer wäre Ihr Kunde, wenn das Projekt auf dem richtigen Weg ist?
Entwickeln Sie einen einfachen, klaren und aufregenden Vorschlag und teilen Sie ihn den Hauptakteuren in Ihrer Organisation mit.
Der beste Weg, um Sponsoren für ein Projekt zu finden, besteht darin, das Problem und das daraus resultierende Datenprodukt nach dessen Implementierung zu verstehen. Dieses Verständnis wird dazu beitragen, das Management von der Bedeutung des Big-Data-Projekts zu überzeugen.
Ein Datenanalyst verfügt über ein berichtsorientiertes Profil und Erfahrung im Extrahieren und Analysieren von Daten aus herkömmlichen Data Warehouses mithilfe von SQL. Ihre Aufgaben liegen normalerweise entweder auf der Seite der Datenspeicherung oder in der Berichterstattung über allgemeine Geschäftsergebnisse. Data Warehousing ist keineswegs einfach, es unterscheidet sich nur von dem, was ein Data Scientist tut.
Viele Unternehmen haben Schwierigkeiten, kompetente Datenwissenschaftler auf dem Markt zu finden. Es ist jedoch eine gute Idee, potenzielle Datenanalysten auszuwählen und ihnen die relevanten Fähigkeiten beizubringen, um Datenwissenschaftler zu werden. Dies ist keineswegs eine triviale Aufgabe und würde normalerweise die Person betreffen, die einen Master-Abschluss in einem quantitativen Bereich macht, aber es ist definitiv eine praktikable Option. Die grundlegenden Fähigkeiten, die ein kompetenter Datenanalyst haben muss, sind nachstehend aufgeführt:
- Geschäftsverständnis
- SQL-Programmierung
- Berichtsgestaltung und -implementierung
- Dashboard-Entwicklung
Die Rolle eines Datenwissenschaftlers ist normalerweise mit Aufgaben wie Vorhersagemodellierung, Entwicklung von Segmentierungsalgorithmen, Empfehlungssystemen, A / B-Test-Frameworks und häufig der Arbeit mit unstrukturierten Rohdaten verbunden.
Die Art ihrer Arbeit erfordert ein tiefes Verständnis von Mathematik, angewandter Statistik und Programmierung. Ein Datenanalyst und ein Datenwissenschaftler haben einige Gemeinsamkeiten, z. B. die Fähigkeit, Datenbanken abzufragen. Beide analysieren Daten, aber die Entscheidung eines Datenwissenschaftlers kann größere Auswirkungen auf eine Organisation haben.
Hier finden Sie eine Reihe von Fähigkeiten, über die ein Datenwissenschaftler normalerweise verfügen muss:
- Programmierung in einem Statistikpaket wie: R, Python, SAS, SPSS oder Julia
- Kann Daten aus verschiedenen Quellen bereinigen, extrahieren und untersuchen
- Forschung, Design und Implementierung statistischer Modelle
- Tiefe statistische, mathematische und Informatikkenntnisse
In der Big-Data-Analyse verwechseln Menschen normalerweise die Rolle eines Datenwissenschaftlers mit der eines Datenarchitekten. In Wirklichkeit ist der Unterschied recht einfach. Ein Datenarchitekt definiert die Werkzeuge und die Architektur, in der die Daten gespeichert werden, während ein Datenwissenschaftler diese Architektur verwendet. Natürlich sollte ein Datenwissenschaftler in der Lage sein, bei Bedarf neue Tools für Ad-hoc-Projekte einzurichten, aber die Definition und das Design der Infrastruktur sollten nicht Teil seiner Aufgabe sein.
In diesem Tutorial werden wir ein Projekt entwickeln. Jedes nachfolgende Kapitel in diesem Tutorial behandelt einen Teil des größeren Projekts im Abschnitt Miniprojekt. Es wird angenommen, dass dies ein angewandter Tutorial-Abschnitt ist, der Aufschluss über ein reales Problem gibt. In diesem Fall würden wir mit der Problemdefinition des Projekts beginnen.
Projektbeschreibung
Ziel dieses Projekts wäre es, ein Modell für maschinelles Lernen zu entwickeln, mit dem das Stundengehalt von Personen anhand ihres Lebenslauftextes als Eingabe vorhergesagt werden kann.
Mit dem oben definierten Framework ist es einfach, das Problem zu definieren. Wir können X = {x 1 , x 2 ,…, x n } als Lebensläufe von Benutzern definieren, wobei jedes Merkmal auf einfachste Weise die Häufigkeit sein kann, mit der dieses Wort vorkommt. Dann ist die Antwort wirklich bewertet, wir versuchen, das Stundengehalt von Einzelpersonen in Dollar vorherzusagen.
Diese beiden Überlegungen reichen aus, um den Schluss zu ziehen, dass das vorgestellte Problem mit einem überwachten Regressionsalgorithmus gelöst werden kann.
Problem Definition
Problem Definitionist wahrscheinlich eine der komplexesten und am meisten vernachlässigten Phasen in der Big-Data-Analyse-Pipeline. Um das Problem zu definieren, das ein Datenprodukt lösen würde, ist Erfahrung erforderlich. Die meisten Aspiranten von Datenwissenschaftlern haben in dieser Phase wenig oder keine Erfahrung.
Die meisten Big-Data-Probleme können folgendermaßen kategorisiert werden:
- Überwachte Klassifizierung
- Überwachte Regression
- Unbeaufsichtigtes Lernen
- Rang lernen lernen
Lassen Sie uns nun mehr über diese vier Konzepte erfahren.
Überwachte Klassifizierung
Ausgehend von einer Matrix von Merkmalen X = {x 1 , x 2 , ..., x n } entwickeln wir ein Modell M, um verschiedene Klassen vorherzusagen, die als y = {c 1 , c 2 , ..., c n } definiert sind . Beispiel: Angesichts der Transaktionsdaten von Kunden in einem Versicherungsunternehmen ist es möglich, ein Modell zu entwickeln, das vorhersagt, ob ein Kunde abwandern würde oder nicht. Letzteres ist ein binäres Klassifizierungsproblem, bei dem es zwei Klassen oder Zielvariablen gibt: Abwanderung und nicht Abwanderung.
Andere Probleme beinhalten die Vorhersage von mehr als einer Klasse. Wir könnten daran interessiert sein, eine Ziffernerkennung durchzuführen. Daher würde der Antwortvektor wie folgt definiert: y = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Ein Modell nach dem Stand der Technik wäre ein Faltungs-Neuronales Netzwerk, und die Matrix von Merkmalen würde als die Pixel des Bildes definiert.
Überwachte Regression
In diesem Fall ist die Problemdefinition dem vorherigen Beispiel ziemlich ähnlich. Der Unterschied hängt von der Antwort ab. In einem Regressionsproblem, der Antwort y ∈ ∈, bedeutet dies, dass die Antwort einen reellen Wert hat. Zum Beispiel können wir ein Modell entwickeln, um das Stundengehalt von Personen anhand des Korpus ihres Lebenslaufs vorherzusagen.
Unbeaufsichtigtes Lernen
Das Management dürstet oft nach neuen Erkenntnissen. Segmentierungsmodelle können diese Erkenntnisse liefern, damit die Marketingabteilung Produkte für verschiedene Segmente entwickeln kann. Ein guter Ansatz für die Entwicklung eines Segmentierungsmodells, anstatt an Algorithmen zu denken, besteht darin, Merkmale auszuwählen, die für die gewünschte Segmentierung relevant sind.
In einem Telekommunikationsunternehmen ist es beispielsweise interessant, Kunden nach ihrer Handynutzung zu segmentieren. Dies würde bedeuten, Features zu ignorieren, die nichts mit dem Segmentierungsziel zu tun haben, und nur diejenigen einzubeziehen, die dies tun. In diesem Fall werden Funktionen wie die Anzahl der in einem Monat verwendeten SMS, die Anzahl der eingehenden und ausgehenden Minuten usw. ausgewählt.
Ranking lernen
Dieses Problem kann als Regressionsproblem angesehen werden, weist jedoch besondere Merkmale auf und verdient eine gesonderte Behandlung. Das Problem besteht darin, dass eine Sammlung von Dokumenten angegeben wird, um bei einer Abfrage die relevanteste Reihenfolge zu finden. Um einen überwachten Lernalgorithmus zu entwickeln, muss angegeben werden, wie relevant eine Bestellung bei einer Abfrage ist.
Es ist wichtig zu beachten, dass zur Entwicklung eines überwachten Lernalgorithmus die Trainingsdaten gekennzeichnet werden müssen. Dies bedeutet, dass wir zum Trainieren eines Modells, das beispielsweise Ziffern aus einem Bild erkennt, eine erhebliche Anzahl von Beispielen von Hand beschriften müssen. Es gibt Webdienste, die diesen Prozess beschleunigen können und häufig für diese Aufgabe verwendet werden, z. B. Amazon Mechanical Turk. Es ist erwiesen, dass Lernalgorithmen ihre Leistung verbessern, wenn sie mit mehr Daten versorgt werden. Daher ist die Kennzeichnung einer angemessenen Anzahl von Beispielen beim überwachten Lernen praktisch obligatorisch.
Die Datenerfassung spielt die wichtigste Rolle im Big Data-Zyklus. Das Internet bietet nahezu unbegrenzte Datenquellen für eine Vielzahl von Themen. Die Bedeutung dieses Bereichs hängt von der Art des Geschäfts ab. Traditionelle Branchen können jedoch eine vielfältige Quelle externer Daten erfassen und diese mit ihren Transaktionsdaten kombinieren.
Nehmen wir zum Beispiel an, wir möchten ein System erstellen, das Restaurants empfiehlt. Der erste Schritt wäre, Daten, in diesem Fall Bewertungen von Restaurants von verschiedenen Websites, zu sammeln und in einer Datenbank zu speichern. Da wir an Rohtext interessiert sind und diesen für die Analyse verwenden würden, ist es nicht so relevant, wo die Daten für die Entwicklung des Modells gespeichert würden. Dies mag im Widerspruch zu den Big-Data-Haupttechnologien klingen, aber um eine Big-Data-Anwendung zu implementieren, müssen sie lediglich in Echtzeit funktionieren.
Twitter Mini-Projekt
Sobald das Problem definiert ist, besteht die folgende Phase darin, die Daten zu sammeln. Die folgende Idee für ein Miniprojekt besteht darin, Daten aus dem Web zu sammeln und zu strukturieren, um sie in einem Modell für maschinelles Lernen zu verwenden. Wir werden einige Tweets von der Twitter Rest API mit der Programmiersprache R sammeln.
Erstellen Sie zunächst ein Twitter-Konto und folgen Sie dann den Anweisungen in der twitteRverpacken Vignette ein Twitter - Entwickler - Konto zu erstellen. Dies ist eine Zusammenfassung dieser Anweisungen -
Gehe zu https://twitter.com/apps/new und einloggen.
Gehen Sie nach dem Ausfüllen der Basisinformationen zur Registerkarte "Einstellungen" und wählen Sie "Direktnachrichten lesen, schreiben und darauf zugreifen".
Stellen Sie sicher, dass Sie danach auf die Schaltfläche Speichern klicken
Notieren Sie auf der Registerkarte "Details" Ihren Verbraucherschlüssel und Ihr Verbrauchergeheimnis
In Ihrer R-Sitzung verwenden Sie den API-Schlüssel und die geheimen API-Werte
Führen Sie abschließend das folgende Skript aus. Dadurch wird das installierttwitteR Paket aus seinem Repository auf Github.
install.packages(c("devtools", "rjson", "bit64", "httr"))
# Make sure to restart your R session at this point
library(devtools)
install_github("geoffjentry/twitteR")Wir sind daran interessiert, Daten zu erhalten, in denen die Zeichenfolge "Big Mac" enthalten ist, und herauszufinden, welche Themen diesbezüglich auffallen. Dazu sammeln Sie zunächst die Daten von Twitter. Unten finden Sie unser R-Skript zum Sammeln der erforderlichen Daten von Twitter. Dieser Code ist auch in der Datei bda / part1 / collect_data / collect_data_twitter.R verfügbar.
rm(list = ls(all = TRUE)); gc() # Clears the global environment
library(twitteR)
Sys.setlocale(category = "LC_ALL", locale = "C")
### Replace the xxx’s with the values you got from the previous instructions
# consumer_key = "xxxxxxxxxxxxxxxxxxxx"
# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# Connect to twitter rest API
setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)
# Get tweets related to big mac
tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)
df <- twListToDF(tweets)
# Take a look at the data
head(df)
# Check which device is most used
sources <- sapply(tweets, function(x) x$getStatusSource())
sources <- gsub("</a>", "", sources)
sources <- strsplit(sources, ">")
sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))
source_table = table(sources)
source_table = source_table[source_table > 1]
freq = source_table[order(source_table, decreasing = T)]
as.data.frame(freq)
# Frequency
# Twitter for iPhone 71
# Twitter for Android 29
# Twitter Web Client 25
# recognia 20Sobald die Daten erfasst sind, verfügen wir normalerweise über verschiedene Datenquellen mit unterschiedlichen Merkmalen. Der unmittelbarste Schritt wäre, diese Datenquellen homogen zu machen und unser Datenprodukt weiterzuentwickeln. Dies hängt jedoch von der Art der Daten ab. Wir sollten uns fragen, ob es praktisch ist, die Daten zu homogenisieren.
Möglicherweise sind die Datenquellen völlig unterschiedlich, und der Informationsverlust ist groß, wenn die Quellen homogenisiert würden. In diesem Fall können wir uns Alternativen vorstellen. Kann mir eine Datenquelle helfen, ein Regressionsmodell und die andere ein Klassifizierungsmodell zu erstellen? Ist es möglich, mit der Heterogenität zu unserem Vorteil zu arbeiten, anstatt nur Informationen zu verlieren? Diese Entscheidungen machen Analytics interessant und herausfordernd.
Bei Überprüfungen ist es möglich, für jede Datenquelle eine Sprache zu haben. Auch hier haben wir zwei Möglichkeiten -
Homogenization- Es geht darum, verschiedene Sprachen in die Sprache zu übersetzen, in der wir mehr Daten haben. Die Qualität der Übersetzungsdienste ist akzeptabel. Wenn wir jedoch große Datenmengen mit einer API übersetzen möchten, sind die Kosten erheblich. Für diese Aufgabe stehen Softwaretools zur Verfügung, aber das wäre auch teuer.
Heterogenization- Wäre es möglich, für jede Sprache eine Lösung zu entwickeln? Da es einfach ist, die Sprache eines Korpus zu erkennen, könnten wir für jede Sprache einen Empfehlungsgeber entwickeln. Dies würde mehr Arbeit in Bezug auf die Abstimmung jedes Empfehlers auf die Anzahl der verfügbaren Sprachen erfordern, ist jedoch definitiv eine praktikable Option, wenn einige Sprachen verfügbar sind.
Twitter Mini-Projekt
Im vorliegenden Fall müssen wir zuerst die unstrukturierten Daten bereinigen und dann in eine Datenmatrix konvertieren, um darauf modellierende Themen anzuwenden. Im Allgemeinen gibt es beim Abrufen von Daten von Twitter mehrere Zeichen, an deren Verwendung wir nicht interessiert sind, zumindest in der ersten Phase des Datenbereinigungsprozesses.
Nach dem Abrufen der Tweets erhalten wir beispielsweise die folgenden seltsamen Zeichen: "<ed> <U + 00A0> <U + 00BD> <ed> <U + 00B8> <U + 008B>". Dies sind wahrscheinlich Emoticons. Um die Daten zu bereinigen, entfernen wir sie einfach mit dem folgenden Skript. Dieser Code ist auch in der Datei bda / part1 / collect_data / cleanging_data.R verfügbar.
rm(list = ls(all = TRUE)); gc() # Clears the global environment
source('collect_data_twitter.R')
# Some tweets
head(df$text)
[1] "I’m not a big fan of turkey but baked Mac &
cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"
[2] "@Jayoh30 Like no special sauce on a big mac. HOW"
### We are interested in the text - Let’s clean it!
# We first convert the encoding of the text from latin1 to ASCII
df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))
# Create a function to clean tweets
clean.text <- function(tx) {
tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)
tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)
tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)
tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)
tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE) return(tx) } clean_tweets <- lapply(df$text, clean.text)
# Cleaned tweets
head(clean_tweets)
[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "
[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "Der letzte Schritt des Datenbereinigungs-Mini-Projekts besteht darin, Text zu bereinigen, den wir in eine Matrix konvertieren und auf den ein Algorithmus angewendet werden kann. Aus dem in derclean_tweets Vektor können wir es leicht in eine Tasche von Wörtern Matrix konvertieren und einen unbeaufsichtigten Lernalgorithmus anwenden.
Die Berichterstellung ist in der Big-Data-Analyse sehr wichtig. Jede Organisation muss regelmäßig Informationen bereitstellen, um ihren Entscheidungsprozess zu unterstützen. Diese Aufgabe wird normalerweise von Datenanalysten mit SQL- und ETL-Erfahrung (Extrahieren, Übertragen und Laden) ausgeführt.
Das für diese Aufgabe zuständige Team ist dafür verantwortlich, die in der Abteilung für Big Data-Analyse erstellten Informationen auf verschiedene Bereiche der Organisation zu verteilen.
Das folgende Beispiel zeigt, was eine Zusammenfassung von Daten bedeutet. Navigieren Sie zum Ordnerbda/part1/summarize_data und öffnen Sie im Ordner die summarize_data.RprojDatei durch Doppelklick darauf. Dann öffnen Sie diesummarize_data.R Skript und werfen Sie einen Blick auf den Code und folgen Sie den Erläuterungen.
# Install the following packages by running the following code in R.
pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')
install.packages(pkgs)Das ggplot2Paket ist ideal für die Datenvisualisierung. Dasdata.table Paket ist eine großartige Option, um eine schnelle und speichereffiziente Zusammenfassung in R. Ein aktueller Benchmark zeigt, dass es noch schneller ist alspandas, die Python-Bibliothek, die für ähnliche Aufgaben verwendet wird.
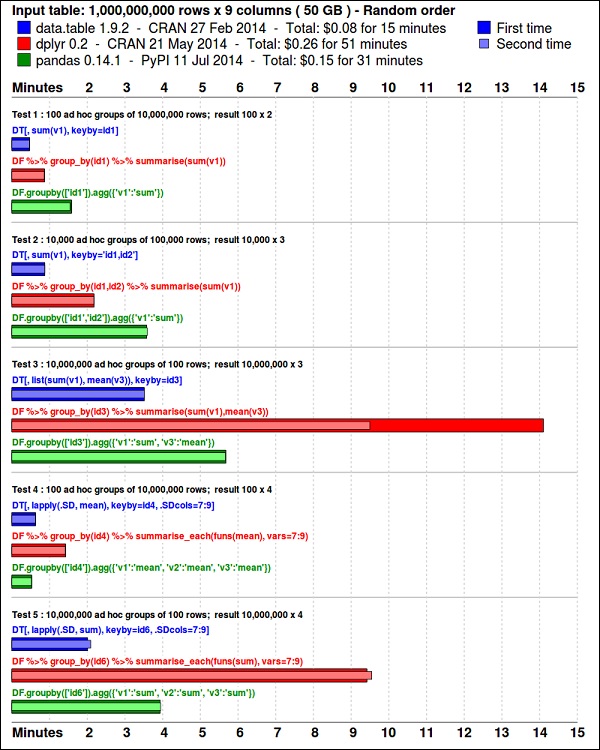
Sehen Sie sich die Daten mit dem folgenden Code an. Dieser Code ist auch in verfügbarbda/part1/summarize_data/summarize_data.Rproj Datei.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Convert the flights data.frame to a data.table object and call it DT
DT <- as.data.table(flights)
# The data has 336776 rows and 16 columns
dim(DT)
# Take a look at the first rows
head(DT)
# year month day dep_time dep_delay arr_time arr_delay carrier
# 1: 2013 1 1 517 2 830 11 UA
# 2: 2013 1 1 533 4 850 20 UA
# 3: 2013 1 1 542 2 923 33 AA
# 4: 2013 1 1 544 -1 1004 -18 B6
# 5: 2013 1 1 554 -6 812 -25 DL
# 6: 2013 1 1 554 -4 740 12 UA
# tailnum flight origin dest air_time distance hour minute
# 1: N14228 1545 EWR IAH 227 1400 5 17
# 2: N24211 1714 LGA IAH 227 1416 5 33
# 3: N619AA 1141 JFK MIA 160 1089 5 42
# 4: N804JB 725 JFK BQN 183 1576 5 44
# 5: N668DN 461 LGA ATL 116 762 5 54
# 6: N39463 1696 EWR ORD 150 719 5 54Der folgende Code enthält ein Beispiel für die Zusammenfassung von Daten.
### Data Summarization
# Compute the mean arrival delay
DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))]
# mean_arrival_delay
# 1: 6.895377
# Now, we compute the same value but for each carrier
mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean1)
# carrier mean_arrival_delay
# 1: UA 3.5580111
# 2: AA 0.3642909
# 3: B6 9.4579733
# 4: DL 1.6443409
# 5: EV 15.7964311
# 6: MQ 10.7747334
# 7: US 2.1295951
# 8: WN 9.6491199
# 9: VX 1.7644644
# 10: FL 20.1159055
# 11: AS -9.9308886
# 12: 9E 7.3796692
# 13: F9 21.9207048
# 14: HA -6.9152047
# 15: YV 15.5569853
# 16: OO 11.9310345
# Now let’s compute to means in the same line of code
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean2)
# carrier mean_departure_delay mean_arrival_delay
# 1: UA 12.106073 3.5580111
# 2: AA 8.586016 0.3642909
# 3: B6 13.022522 9.4579733
# 4: DL 9.264505 1.6443409
# 5: EV 19.955390 15.7964311
# 6: MQ 10.552041 10.7747334
# 7: US 3.782418 2.1295951
# 8: WN 17.711744 9.6491199
# 9: VX 12.869421 1.7644644
# 10: FL 18.726075 20.1159055
# 11: AS 5.804775 -9.9308886
# 12: 9E 16.725769 7.3796692
# 13: F9 20.215543 21.9207048
# 14: HA 4.900585 -6.9152047
# 15: YV 18.996330 15.5569853
# 16: OO 12.586207 11.9310345
### Create a new variable called gain
# this is the difference between arrival delay and departure delay
DT[, gain:= arr_delay - dep_delay]
# Compute the median gain per carrier
median_gain = DT[, median(gain, na.rm = TRUE), by = carrier]
print(median_gain)Exploratory data analysisist ein von John Tuckey (1977) entwickeltes Konzept, das auf einer neuen Perspektive der Statistik besteht. Tuckeys Idee war, dass in der traditionellen Statistik die Daten nicht grafisch untersucht wurden, sondern nur zum Testen von Hypothesen verwendet wurden. Der erste Versuch, ein Tool zu entwickeln, wurde in Stanford unternommen . Das Projekt hieß prim9 . Das Tool konnte Daten in neun Dimensionen visualisieren und somit eine multivariate Perspektive der Daten bieten.
In den letzten Tagen ist die explorative Datenanalyse ein Muss und wurde in den Lebenszyklus der Big-Data-Analyse aufgenommen. Die Fähigkeit, Erkenntnisse zu finden und diese in einem Unternehmen effektiv zu kommunizieren, wird durch starke EDA-Fähigkeiten unterstützt.
Basierend auf Tuckeys Ideen entwickelten Bell Labs das S programming languageum eine interaktive Schnittstelle für die Erstellung von Statistiken bereitzustellen. Die Idee von S war es, umfangreiche grafische Funktionen mit einer benutzerfreundlichen Sprache bereitzustellen. In der heutigen Welt, im Kontext von Big Data,R das basiert auf dem S Die Programmiersprache ist die beliebteste Software für die Analyse.
Das folgende Programm demonstriert die Verwendung der explorativen Datenanalyse.
Das Folgende ist ein Beispiel für eine explorative Datenanalyse. Dieser Code ist auch in verfügbarpart1/eda/exploratory_data_analysis.R Datei.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Using the code from the previous section
# This computes the mean arrival and departure delays by carrier.
DT <- as.data.table(flights)
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
# In order to plot data in R usign ggplot, it is normally needed to reshape the data
# We want to have the data in long format for plotting with ggplot
dt = melt(mean2, id.vars = ’carrier’)
# Take a look at the first rows
print(head(dt))
# Take a look at the help for ?geom_point and geom_line to find similar examples
# Here we take the carrier code as the x axis
# the value from the dt data.table goes in the y axis
# The variable column represents the color
p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +
geom_point() + # Plots points
geom_line() + # Plots lines
theme_bw() + # Uses a white background
labs(list(title = 'Mean arrival and departure delay by carrier',
x = 'Carrier', y = 'Mean delay'))
print(p)
# Save the plot to disk
ggsave('mean_delay_by_carrier.png', p,
width = 10.4, height = 5.07)Der Code sollte ein Bild wie das folgende erzeugen:

Um Daten zu verstehen, ist es oft nützlich, sie zu visualisieren. Normalerweise besteht das Interesse an Big-Data-Anwendungen darin, Erkenntnisse zu gewinnen und nicht nur schöne Diagramme zu erstellen. Im Folgenden finden Sie Beispiele für verschiedene Ansätze zum Verständnis von Daten mithilfe von Diagrammen.
Um mit der Analyse der Flugdaten zu beginnen, können wir zunächst prüfen, ob Korrelationen zwischen numerischen Variablen bestehen. Dieser Code ist auch in verfügbarbda/part1/data_visualization/data_visualization.R Datei.
# Install the package corrplot by running
install.packages('corrplot')
# then load the library
library(corrplot)
# Load the following libraries
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# We will continue working with the flights data
DT <- as.data.table(flights)
head(DT) # take a look
# We select the numeric variables after inspecting the first rows.
numeric_variables = c('dep_time', 'dep_delay',
'arr_time', 'arr_delay', 'air_time', 'distance')
# Select numeric variables from the DT data.table
dt_num = DT[, numeric_variables, with = FALSE]
# Compute the correlation matrix of dt_num
cor_mat = cor(dt_num, use = "complete.obs")
print(cor_mat)
### Here is the correlation matrix
# dep_time dep_delay arr_time arr_delay air_time distance
# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373
# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090
# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917
# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776
# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965
# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000
# We can display it visually to get a better understanding of the data
corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")
# save it to disk
png('corrplot.png')
print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))
dev.off()Dieser Code generiert die folgende Korrelationsmatrix-Visualisierung:

In der Darstellung sehen wir, dass zwischen einigen Variablen im Datensatz eine starke Korrelation besteht. Zum Beispiel scheinen Ankunfts- und Abflugverzögerung stark korreliert zu sein. Wir können dies sehen, weil die Ellipse eine fast lineare Beziehung zwischen beiden Variablen zeigt, es jedoch nicht einfach ist, aus diesem Ergebnis eine Ursache zu finden.
Wir können nicht sagen, dass zwei Variablen miteinander korrelieren und dass sich eine auf die andere auswirkt. Außerdem finden wir in der Darstellung eine starke Korrelation zwischen Sendezeit und Entfernung, was ziemlich vernünftig zu erwarten ist, da mit zunehmender Entfernung die Flugzeit zunehmen sollte.
Wir können auch eine univariate Analyse der Daten durchführen. Eine einfache und effektive Möglichkeit, Verteilungen zu visualisieren, sindbox-plots. Der folgende Code zeigt, wie Box-Plots und Trellis-Diagramme mithilfe der ggplot2-Bibliothek erstellt werden. Dieser Code ist auch in verfügbarbda/part1/data_visualization/boxplots.R Datei.
source('data_visualization.R')
### Analyzing Distributions using box-plots
# The following shows the distance as a function of the carrier
p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier
in the x axis and distance in the y axis
geom_box-plot() + # Use the box-plot geom
theme_bw() + # Leave a white background - More in line with tufte's
principles than the default
guides(fill = FALSE) + # Remove legend
labs(list(title = 'Distance as a function of carrier', # Add labels
x = 'Carrier', y = 'Distance'))
p
# Save to disk
png(‘boxplot_carrier.png’)
print(p)
dev.off()
# Let's add now another variable, the month of each flight
# We will be using facet_wrap for this
p = ggplot(DT, aes(carrier, distance, fill = carrier)) +
geom_box-plot() +
theme_bw() +
guides(fill = FALSE) +
facet_wrap(~month) + # This creates the trellis plot with the by month variable
labs(list(title = 'Distance as a function of carrier by month',
x = 'Carrier', y = 'Distance'))
p
# The plot shows there aren't clear differences between distance in different months
# Save to disk
png('boxplot_carrier_by_month.png')
print(p)
dev.off()Dieser Abschnitt ist dazu gedacht, den Benutzern die Programmiersprache R vorzustellen. R kann von der Cran-Website heruntergeladen werden . Für Windows-Benutzer ist es hilfreich, rtools und die rstudio-IDE zu installieren .
Das allgemeine Konzept dahinter R soll als Schnittstelle zu anderer Software dienen, die in kompilierten Sprachen wie C, C ++ und Fortran entwickelt wurde, und dem Benutzer ein interaktives Tool zur Datenanalyse bieten.
Navigieren Sie zum Ordner der Buch-Zip-Datei bda/part2/R_introduction und öffnen Sie die R_introduction.RprojDatei. Dadurch wird eine RStudio-Sitzung geöffnet. Öffnen Sie dann die Datei 01_vectors.R. Führen Sie das Skript Zeile für Zeile aus und folgen Sie den Kommentaren im Code. Eine weitere nützliche Option zum Lernen besteht darin, nur den Code einzugeben. Dies hilft Ihnen, sich an die R-Syntax zu gewöhnen. In R werden Kommentare mit dem Symbol # geschrieben.
Um die Ergebnisse der Ausführung von R-Code im Buch anzuzeigen, werden nach der Auswertung des Codes die Ergebnisse, die R zurückgibt, kommentiert. Auf diese Weise können Sie den Code kopieren, in das Buch einfügen und direkt Abschnitte davon in R ausprobieren.
# Create a vector of numbers
numbers = c(1, 2, 3, 4, 5)
print(numbers)
# [1] 1 2 3 4 5
# Create a vector of letters
ltrs = c('a', 'b', 'c', 'd', 'e')
# [1] "a" "b" "c" "d" "e"
# Concatenate both
mixed_vec = c(numbers, ltrs)
print(mixed_vec)
# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"Lassen Sie uns analysieren, was im vorherigen Code passiert ist. Wir können sehen, dass es möglich ist, Vektoren mit Zahlen und Buchstaben zu erstellen. Wir mussten R nicht vorher mitteilen, welchen Datentyp wir wollten. Schließlich konnten wir einen Vektor mit Zahlen und Buchstaben erstellen. Der Vektor gemischte_vec hat die Zahlen zum Zeichen gezwungen. Wir können dies sehen, indem wir visualisieren, wie die Werte in Anführungszeichen gedruckt werden.
Der folgende Code zeigt den Datentyp verschiedener Vektoren, wie er von der Funktionsklasse zurückgegeben wird. Es ist üblich, die Klassenfunktion zu verwenden, um ein Objekt "abzufragen" und ihn zu fragen, was seine Klasse ist.
### Evaluate the data types using class
### One dimensional objects
# Integer vector
num = 1:10
class(num)
# [1] "integer"
# Numeric vector, it has a float, 10.5
num = c(1:10, 10.5)
class(num)
# [1] "numeric"
# Character vector
ltrs = letters[1:10]
class(ltrs)
# [1] "character"
# Factor vector
fac = as.factor(ltrs)
class(fac)
# [1] "factor"R unterstützt auch zweidimensionale Objekte. Im folgenden Code finden Sie Beispiele für die beiden beliebtesten Datenstrukturen, die in R verwendet werden: die Matrix und data.frame.
# Matrix
M = matrix(1:12, ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] 1 4 7 10
# [2,] 2 5 8 11
# [3,] 3 6 9 12
lM = matrix(letters[1:12], ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] "a" "d" "g" "j"
# [2,] "b" "e" "h" "k"
# [3,] "c" "f" "i" "l"
# Coerces the numbers to character
# cbind concatenates two matrices (or vectors) in one matrix
cbind(M, lM)
# [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
# [1,] "1" "4" "7" "10" "a" "d" "g" "j"
# [2,] "2" "5" "8" "11" "b" "e" "h" "k"
# [3,] "3" "6" "9" "12" "c" "f" "i" "l"
class(M)
# [1] "matrix"
class(lM)
# [1] "matrix"
# data.frame
# One of the main objects of R, handles different data types in the same object.
# It is possible to have numeric, character and factor vectors in the same data.frame
df = data.frame(n = 1:5, l = letters[1:5])
df
# n l
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 eWie im vorherigen Beispiel gezeigt, können im selben Objekt unterschiedliche Datentypen verwendet werden. Im Allgemeinen werden Daten auf diese Weise in Datenbanken dargestellt. APIs Teil der Daten sind Text- oder Zeichenvektoren und andere numerische Elemente. In ist der Analystenjob, um zu bestimmen, welcher statistische Datentyp zugewiesen werden soll, und dann den richtigen R-Datentyp dafür zu verwenden. In der Statistik betrachten wir normalerweise Variablen vom folgenden Typ:
- Numeric
- Nominal oder kategorisch
- Ordinal
In R kann ein Vektor der folgenden Klassen angehören:
- Numerisch - Ganzzahl
- Factor
- Bestellfaktor
R liefert einen Datentyp für jeden statistischen Variablentyp. Der geordnete Faktor wird jedoch selten verwendet, kann jedoch durch den Funktionsfaktor erstellt oder geordnet werden.
Der folgende Abschnitt behandelt das Konzept der Indizierung. Dies ist eine recht häufige Operation und befasst sich mit dem Problem, Abschnitte eines Objekts auszuwählen und Transformationen an ihnen vorzunehmen.
# Let's create a data.frame
df = data.frame(numbers = 1:26, letters)
head(df)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# str gives the structure of a data.frame, it’s a good summary to inspect an object
str(df)
# 'data.frame': 26 obs. of 2 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ... # $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# The latter shows the letters character vector was coerced as a factor.
# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame
# read ?data.frame for more information
class(df)
# [1] "data.frame"
### Indexing
# Get the first row
df[1, ]
# numbers letters
# 1 1 a
# Used for programming normally - returns the output as a list
df[1, , drop = TRUE]
# $numbers # [1] 1 # # $letters
# [1] a
# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z
# Get several rows of the data.frame
df[5:7, ]
# numbers letters
# 5 5 e
# 6 6 f
# 7 7 g
### Add one column that mixes the numeric column with the factor column
df$mixed = paste(df$numbers, df$letters, sep = ’’) str(df) # 'data.frame': 26 obs. of 3 variables: # $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ... # $ mixed : chr "1a" "2b" "3c" "4d" ...
### Get columns
# Get the first column
df[, 1]
# It returns a one dimensional vector with that column
# Get two columns
df2 = df[, 1:2]
head(df2)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# Get the first and third columns
df3 = df[, c(1, 3)]
df3[1:3, ]
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
### Index columns from their names
names(df)
# [1] "numbers" "letters" "mixed"
# This is the best practice in programming, as many times indeces change, but
variable names don’t
# We create a variable with the names we want to subset
keep_vars = c("numbers", "mixed")
df4 = df[, keep_vars]
head(df4)
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
### subset rows and columns
# Keep the first five rows
df5 = df[1:5, keep_vars]
df5
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# subset rows using a logical condition
df6 = df[df$numbers < 10, keep_vars]
df6
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
# 7 7 7g
# 8 8 8h
# 9 9 9iSQL steht für strukturierte Abfragesprache. Es ist eine der am häufigsten verwendeten Sprachen zum Extrahieren von Daten aus Datenbanken in traditionellen Data Warehouses und Big Data-Technologien. Um die Grundlagen von SQL zu demonstrieren, werden wir mit Beispielen arbeiten. Um uns auf die Sprache selbst zu konzentrieren, werden wir SQL in R verwenden. Beim Schreiben von SQL-Code ist dies genau so, wie es in einer Datenbank geschehen würde.
Der Kern von SQL sind drei Anweisungen: SELECT, FROM und WHERE. In den folgenden Beispielen werden die häufigsten Anwendungsfälle von SQL verwendet. Navigieren Sie zum Ordnerbda/part2/SQL_introduction und öffnen Sie die SQL_introduction.RprojDatei. Öffnen Sie dann das Skript 01_select.R. Um SQL-Code in R zu schreiben, müssen wir den installierensqldf Paket wie im folgenden Code gezeigt.
# Install the sqldf package
install.packages('sqldf')
# load the library
library('sqldf')
library(nycflights13)
# We will be working with the fligths dataset in order to introduce SQL
# Let’s take a look at the table
str(flights)
# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:
# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
# $ month : int 1 1 1 1 1 1 1 1 1 1 ... # $ day : int 1 1 1 1 1 1 1 1 1 1 ...
# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ... # $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ... # $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...
# $ carrier : chr "UA" "UA" "AA" "B6" ... # $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...
# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ... # $ origin : chr "EWR" "LGA" "JFK" "JFK" ...
# $ dest : chr "IAH" "IAH" "MIA" "BQN" ... # $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...
# $ distance : num 1400 1416 1089 1576 762 ... # $ hour : num 5 5 5 5 5 5 5 5 5 5 ...
# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...Die select-Anweisung wird verwendet, um Spalten aus Tabellen abzurufen und Berechnungen an ihnen durchzuführen. Die einfachste SELECT-Anweisung wird in demonstriertej1. Wir können auch neue Variablen erstellen, wie in gezeigtej2.
### SELECT statement
ej1 = sqldf("
SELECT
dep_time
,dep_delay
,arr_time
,carrier
,tailnum
FROM
flights
")
head(ej1)
# dep_time dep_delay arr_time carrier tailnum
# 1 517 2 830 UA N14228
# 2 533 4 850 UA N24211
# 3 542 2 923 AA N619AA
# 4 544 -1 1004 B6 N804JB
# 5 554 -6 812 DL N668DN
# 6 554 -4 740 UA N39463
# In R we can use SQL with the sqldf function. It works exactly the same as in
a database
# The data.frame (in this case flights) represents the table we are querying
and goes in the FROM statement
# We can also compute new variables in the select statement using the syntax:
# old_variables as new_variable
ej2 = sqldf("
SELECT
arr_delay - dep_delay as gain,
carrier
FROM
flights
")
ej2[1:5, ]
# gain carrier
# 1 9 UA
# 2 16 UA
# 3 31 AA
# 4 -17 B6
# 5 -19 DLEine der am häufigsten verwendeten Funktionen von SQL ist die Anweisung group by. Dies ermöglicht die Berechnung eines numerischen Werts für verschiedene Gruppen einer anderen Variablen. Öffnen Sie das Skript 02_group_by.R.
### GROUP BY
# Computing the average
ej3 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
avg(dep_delay) as mean_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# mean_arr_delay mean_dep_delay carrier
# 1 7.3796692 16.725769 9E
# 2 0.3642909 8.586016 AA
# 3 -9.9308886 5.804775 AS
# 4 9.4579733 13.022522 B6
# 5 1.6443409 9.264505 DL
# 6 15.7964311 19.955390 EV
# 7 21.9207048 20.215543 F9
# 8 20.1159055 18.726075 FL
# 9 -6.9152047 4.900585 HA
# 10 10.7747334 10.552041 MQ
# 11 11.9310345 12.586207 OO
# 12 3.5580111 12.106073 UA
# 13 2.1295951 3.782418 US
# 14 1.7644644 12.869421 VX
# 15 9.6491199 17.711744 WN
# 16 15.5569853 18.996330 YV
# Other aggregations
ej4 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
min(dep_delay) as min_dep_delay,
max(dep_delay) as max_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# We can compute the minimun, mean, and maximum values of a numeric value
ej4
# mean_arr_delay min_dep_delay max_dep_delay carrier
# 1 7.3796692 -24 747 9E
# 2 0.3642909 -24 1014 AA
# 3 -9.9308886 -21 225 AS
# 4 9.4579733 -43 502 B6
# 5 1.6443409 -33 960 DL
# 6 15.7964311 -32 548 EV
# 7 21.9207048 -27 853 F9
# 8 20.1159055 -22 602 FL
# 9 -6.9152047 -16 1301 HA
# 10 10.7747334 -26 1137 MQ
# 11 11.9310345 -14 154 OO
# 12 3.5580111 -20 483 UA
# 13 2.1295951 -19 500 US
# 14 1.7644644 -20 653 VX
# 15 9.6491199 -13 471 WN
# 16 15.5569853 -16 387 YV
### We could be also interested in knowing how many observations each carrier has
ej5 = sqldf("
SELECT
carrier, count(*) as count
FROM
flights
GROUP BY
carrier
")
ej5
# carrier count
# 1 9E 18460
# 2 AA 32729
# 3 AS 714
# 4 B6 54635
# 5 DL 48110
# 6 EV 54173
# 7 F9 685
# 8 FL 3260
# 9 HA 342
# 10 MQ 26397
# 11 OO 32
# 12 UA 58665
# 13 US 20536
# 14 VX 5162
# 15 WN 12275
# 16 YV 601Die nützlichste Funktion von SQL sind Verknüpfungen. Ein Join bedeutet, dass wir Tabelle A und Tabelle B in einer Tabelle unter Verwendung einer Spalte kombinieren möchten, um die Werte beider Tabellen abzugleichen. In der Praxis gibt es verschiedene Arten von Verknüpfungen. Zu Beginn sind dies die nützlichsten: innere Verknüpfung und linke äußere Verknüpfung.
# Let’s create two tables: A and B to demonstrate joins.
A = data.frame(c1 = 1:4, c2 = letters[1:4])
B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])
A
# c1 c2
# 1 a
# 2 b
# 3 c
# 4 d
B
# c1 c2
# 2 b
# 4 c
# 5 d
# 6 e
### INNER JOIN
# This means to match the observations of the column we would join the tables by.
inner = sqldf("
SELECT
A.c1, B.c2
FROM
A INNER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
inner
# c1 c2
# 2 b
# 4 c
### LEFT OUTER JOIN
# the left outer join, sometimes just called left join will return the
# first all the values of the column used from the A table
left = sqldf("
SELECT
A.c1, B.c2
FROM
A LEFT OUTER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
left
# c1 c2
# 1 <NA>
# 2 b
# 3 <NA>
# 4 cDer erste Ansatz zur Analyse von Daten besteht darin, sie visuell zu analysieren. Die Ziele dabei sind normalerweise das Finden von Beziehungen zwischen Variablen und univariaten Beschreibungen der Variablen. Wir können diese Strategien wie folgt aufteilen:
- Univariate Analyse
- Multivariate Analyse
Univariate grafische Methoden
Univariateist ein statistischer Begriff. In der Praxis bedeutet dies, dass wir eine Variable unabhängig von den übrigen Daten analysieren möchten. Die Grundstücke, die dies effizient ermöglichen, sind:
Box-Plots
Box-Plots werden normalerweise zum Vergleichen von Verteilungen verwendet. Es ist eine großartige Möglichkeit, visuell zu prüfen, ob es Unterschiede zwischen den Verteilungen gibt. Wir können sehen, ob es Unterschiede zwischen dem Preis von Diamanten für verschiedenen Schliff gibt.
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)Wir können in der Darstellung sehen, dass es Unterschiede in der Verteilung des Diamantenpreises in verschiedenen Schliffarten gibt.

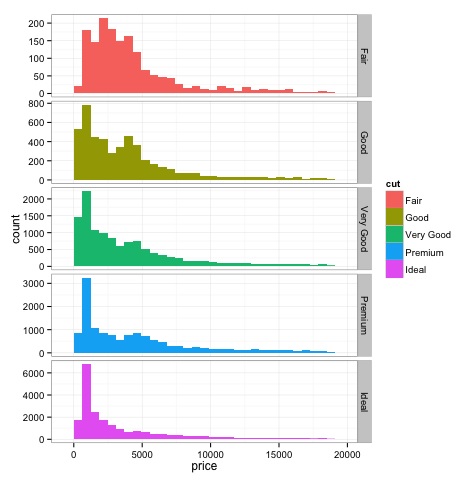
Histogramme
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()Die Ausgabe des obigen Codes lautet wie folgt:
Multivariate grafische Methoden
Multivariate grafische Methoden in der explorativen Datenanalyse haben das Ziel, Beziehungen zwischen verschiedenen Variablen zu finden. Es gibt zwei Möglichkeiten, um dies zu erreichen, die üblicherweise verwendet werden: Zeichnen einer Korrelationsmatrix numerischer Variablen oder einfaches Zeichnen der Rohdaten als Matrix von Streudiagrammen.
Um dies zu demonstrieren, verwenden wir den Diamanten-Datensatz. Öffnen Sie das Skript, um dem Code zu folgenbda/part2/charts/03_multivariate_analysis.R.
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)Der Code erzeugt die folgende Ausgabe -

Dies ist eine Zusammenfassung, die uns sagt, dass es eine starke Korrelation zwischen Preis und Caret gibt und nicht viel zwischen den anderen Variablen.
Eine Korrelationsmatrix kann nützlich sein, wenn wir eine große Anzahl von Variablen haben. In diesem Fall wäre das Zeichnen der Rohdaten nicht praktikabel. Wie bereits erwähnt, können die Rohdaten auch angezeigt werden -
library(GGally)
ggpairs(df)Wir können in der Darstellung sehen, dass die in der Wärmekarte angezeigten Ergebnisse bestätigt sind, es gibt eine Korrelation von 0,922 zwischen den Preis- und Karatvariablen.
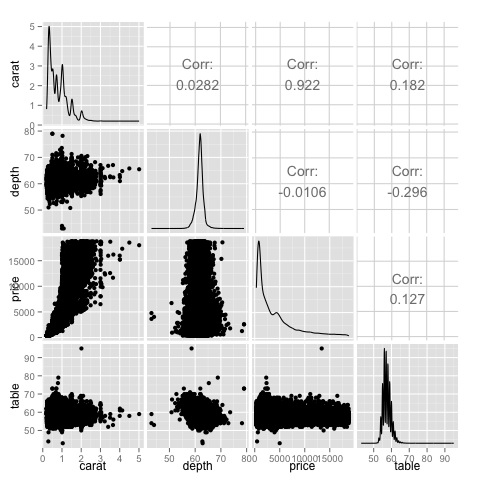
Es ist möglich, diese Beziehung im Preis-Karat-Streudiagramm zu visualisieren, das sich im (3, 1) -Index der Streudiagrammmatrix befindet.
Es gibt eine Vielzahl von Tools, mit denen ein Datenwissenschaftler Daten effektiv analysieren kann. Normalerweise konzentriert sich der technische Aspekt der Datenanalyse auf Datenbanken, der Schwerpunkt der Datenwissenschaftler auf Tools, die Datenprodukte implementieren können. Im folgenden Abschnitt werden die Vorteile verschiedener Tools erläutert, wobei der Schwerpunkt auf statistischen Paketen liegt, die Datenwissenschaftler in der Praxis am häufigsten verwenden.
R Programmiersprache
R ist eine Open-Source-Programmiersprache mit Schwerpunkt auf statistischer Analyse. In Bezug auf statistische Funktionen ist es mit kommerziellen Tools wie SAS und SPSS konkurrenzfähig. Es wird angenommen, dass es eine Schnittstelle zu anderen Programmiersprachen wie C, C ++ oder Fortran ist.
Ein weiterer Vorteil von R ist die große Anzahl verfügbarer Open Source-Bibliotheken. In CRAN gibt es mehr als 6000 Pakete, die kostenlos und in heruntergeladen werden könnenGithub Es gibt eine Vielzahl von R-Paketen.
In Bezug auf die Leistung ist R für intensive Operationen langsam, da aufgrund der großen Anzahl verfügbarer Bibliotheken die langsamen Abschnitte des Codes in kompilierten Sprachen geschrieben sind. Wenn Sie jedoch Operationen ausführen möchten, bei denen für Schleifen tief geschrieben werden muss, ist R nicht die beste Alternative. Für Datenanalysezwecke gibt es nette Bibliotheken wiedata.table, glmnet, ranger, xgboost, ggplot2, caret die es ermöglichen, R als Schnittstelle zu schnelleren Programmiersprachen zu verwenden.
Python zur Datenanalyse
Python ist eine Allzweck-Programmiersprache und enthält eine erhebliche Anzahl von Bibliotheken, die sich der Datenanalyse widmen, wie z pandas, scikit-learn, theano, numpy und scipy.
Das meiste, was in R verfügbar ist, kann auch in Python ausgeführt werden, aber wir haben festgestellt, dass R einfacher zu verwenden ist. Wenn Sie mit großen Datenmengen arbeiten, ist Python normalerweise die bessere Wahl als R. Python kann sehr effektiv verwendet werden, um Daten Zeile für Zeile zu bereinigen und zu verarbeiten. Dies ist ab R möglich, aber für Skriptaufgaben nicht so effizient wie Python.
Für maschinelles Lernen scikit-learnist eine schöne Umgebung, die eine große Anzahl von Algorithmen zur Verfügung hat, die problemlos mittelgroße Datensätze verarbeiten können. Im Vergleich zu Rs äquivalenter Bibliothek (Caret),scikit-learn hat eine sauberere und konsistentere API.
Julia
Julia ist eine leistungsstarke dynamische Programmiersprache für das technische Rechnen. Die Syntax ist R oder Python sehr ähnlich. Wenn Sie also bereits mit R oder Python arbeiten, sollte es recht einfach sein, denselben Code in Julia zu schreiben. Die Sprache ist ziemlich neu und in den letzten Jahren erheblich gewachsen, daher ist sie im Moment definitiv eine Option.
Wir würden Julia für rechenintensive Prototyping-Algorithmen wie neuronale Netze empfehlen. Es ist ein großartiges Werkzeug für die Forschung. In Bezug auf die Implementierung eines Modells in der Produktion hat Python wahrscheinlich bessere Alternativen. Dies wird jedoch immer weniger problematisch, da es Webdienste gibt, die die Implementierung von Modellen in R, Python und Julia durchführen.
SAS
SAS ist eine Handelssprache, die immer noch für Business Intelligence verwendet wird. Es verfügt über eine Basissprache, mit der der Benutzer eine Vielzahl von Anwendungen programmieren kann. Es enthält einige kommerzielle Produkte, mit denen Nicht-Experten komplexe Tools wie eine neuronale Netzwerkbibliothek verwenden können, ohne programmieren zu müssen.
Abgesehen von dem offensichtlichen Nachteil kommerzieller Tools lässt sich SAS nicht gut auf große Datenmengen skalieren. Selbst mittelgroße Datasets haben Probleme mit SAS und führen zum Absturz des Servers. Nur wenn Sie mit kleinen Datenmengen arbeiten und die Benutzer keine erfahrenen Datenwissenschaftler sind, ist SAS zu empfehlen. Für fortgeschrittene Benutzer bieten R und Python eine produktivere Umgebung.
SPSS
SPSS ist derzeit ein Produkt von IBM für statistische Analysen. Es wird hauptsächlich zur Analyse von Umfragedaten verwendet und ist für Benutzer, die nicht programmieren können, eine anständige Alternative. Es ist wahrscheinlich so einfach zu verwenden wie SAS, aber in Bezug auf die Implementierung eines Modells ist es einfacher, da es einen SQL-Code zum Bewerten eines Modells bereitstellt. Dieser Code ist normalerweise nicht effizient, aber es ist ein Anfang, während SAS das Produkt verkauft, das Modelle für jede Datenbank separat bewertet. Für kleine Datenmengen und ein unerfahrenes Team ist SPSS eine ebenso gute Option wie SAS.
Die Software ist jedoch eher begrenzt, und erfahrene Benutzer sind mit R oder Python um Größenordnungen produktiver.
Matlab, Oktave
Es gibt andere Tools wie Matlab oder seine Open Source-Version (Octave). Diese Werkzeuge werden hauptsächlich für Forschungszwecke verwendet. In Bezug auf die Funktionen können R oder Python alles tun, was in Matlab oder Octave verfügbar ist. Es ist nur dann sinnvoll, eine Lizenz für das Produkt zu kaufen, wenn Sie an der Unterstützung interessiert sind, die sie bieten.
Bei der Analyse von Daten ist ein statistischer Ansatz möglich. Die grundlegenden Werkzeuge, die zur Durchführung der grundlegenden Analyse benötigt werden, sind:
- Korrelationsanalyse
- Varianzanalyse
- Hypothesentest
Bei der Arbeit mit großen Datenmengen ist dies kein Problem, da diese Methoden mit Ausnahme der Korrelationsanalyse nicht rechenintensiv sind. In diesem Fall ist es immer möglich, eine Probe zu entnehmen, und die Ergebnisse sollten robust sein.
Korrelationsanalyse
Die Korrelationsanalyse versucht, lineare Beziehungen zwischen numerischen Variablen zu finden. Dies kann unter verschiedenen Umständen von Nutzen sein. Eine häufige Verwendung ist die explorative Datenanalyse. In Abschnitt 16.0.2 des Buches gibt es ein grundlegendes Beispiel für diesen Ansatz. Zunächst basiert die im genannten Beispiel verwendete Korrelationsmetrik auf derPearson coefficient. Es gibt jedoch eine andere interessante Korrelationsmetrik, die von Ausreißern nicht beeinflusst wird. Diese Metrik wird als Spearman-Korrelation bezeichnet.
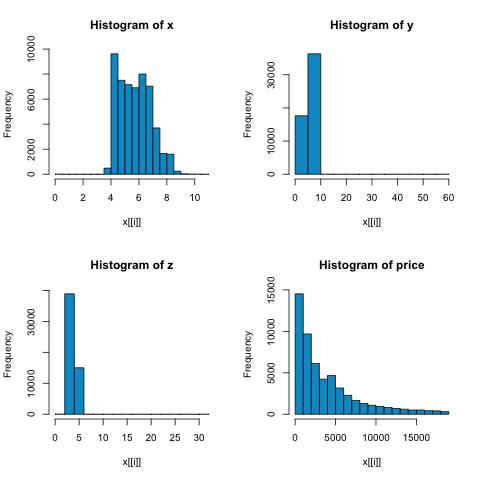
Das spearman correlation Die Metrik ist gegenüber Ausreißern robuster als die Pearson-Methode und liefert bessere Schätzungen der linearen Beziehungen zwischen numerischen Variablen, wenn die Daten nicht normal verteilt sind.
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))Aus den Histogrammen in der folgenden Abbildung können wir Unterschiede in den Korrelationen beider Metriken erwarten. In diesem Fall ist die Spearman-Korrelation eine bessere Schätzung der linearen Beziehung zwischen numerischen Variablen, da die Variablen eindeutig nicht normalverteilt sind.
Öffnen Sie die Datei, um die Korrelation in R zu berechnen bda/part2/statistical_methods/correlation/correlation.R das hat diesen Codeabschnitt.
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000Chi-Quadrat-Test
Mit dem Chi-Quadrat-Test können wir testen, ob zwei Zufallsvariablen unabhängig sind. Dies bedeutet, dass die Wahrscheinlichkeitsverteilung jeder Variablen die andere nicht beeinflusst. Um den Test in R auszuwerten, müssen wir zuerst eine Kontingenztabelle erstellen und dann die Tabelle an die übergebenchisq.test R Funktion.
Lassen Sie uns beispielsweise prüfen, ob zwischen den Variablen: Schnitt und Farbe aus dem Diamanten-Dataset eine Zuordnung besteht. Der Test ist formal definiert als -
- H0: Der variable Schliff und der Diamant sind unabhängig voneinander
- H1: Der variable Schliff und der Diamant sind nicht unabhängig voneinander
Wir würden annehmen, dass es eine Beziehung zwischen diesen beiden Variablen durch ihren Namen gibt, aber der Test kann eine objektive "Regel" geben, die besagt, wie signifikant dieses Ergebnis ist oder nicht.
Im folgenden Codeausschnitt haben wir festgestellt, dass der p-Wert des Tests 2,2e-16 beträgt, dies ist praktisch nahezu Null. Dann nach dem Ausführen des Tests aMonte Carlo simulationfanden wir, dass der p-Wert 0,0004998 ist, was immer noch ziemlich niedriger als der Schwellenwert 0,05 ist. Dieses Ergebnis bedeutet, dass wir die Nullhypothese (H0) ablehnen, also glauben wir den Variablencut und color sind nicht unabhängig.
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998T-Test
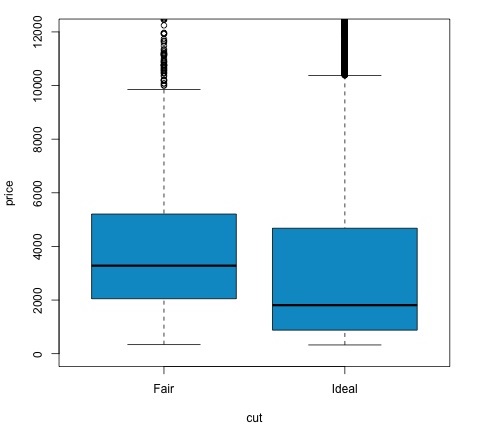
Die Idee von t-testist zu bewerten, ob es Unterschiede in der Verteilung der numerischen Variablen # zwischen verschiedenen Gruppen einer nominalen Variablen gibt. Um dies zu demonstrieren, werde ich die Ebenen der fairen und idealen Ebenen der Faktorvariablen abschneiden und dann die Werte einer numerischen Variablen zwischen diesen beiden Gruppen vergleichen.
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542Die t-Tests werden in R mit dem implementiert t.testFunktion. Die Formelschnittstelle zu t.test ist die einfachste Möglichkeit, sie zu verwenden. Die Idee ist, dass eine numerische Variable durch eine Gruppenvariable erklärt wird.
Zum Beispiel: t.test(numeric_variable ~ group_variable, data = data). Im vorherigen Beispiel wurde dienumeric_variable ist price und die group_variable ist cut.
Aus statistischer Sicht testen wir, ob es Unterschiede in der Verteilung der numerischen Variablen zwischen zwei Gruppen gibt. Formal wird der Hypothesentest mit einer Nullhypothese (H0) und einer Alternativhypothese (H1) beschrieben.
H0: Es gibt keine Unterschiede in der Verteilung der Preisvariablen zwischen den Gruppen Fair und Ideal
H1 Es gibt Unterschiede in der Verteilung der Preisvariablen zwischen den Gruppen Fair und Ideal
Folgendes kann in R mit dem folgenden Code implementiert werden:
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')Wir können das Testergebnis analysieren, indem wir prüfen, ob der p-Wert unter 0,05 liegt. In diesem Fall behalten wir die alternative Hypothese bei. Dies bedeutet, dass wir Preisunterschiede zwischen den beiden Ebenen des Schnittfaktors festgestellt haben. Bei den Namen der Ebenen hätten wir dieses Ergebnis erwartet, aber wir hätten nicht erwartet, dass der Durchschnittspreis in der Fail-Gruppe höher wäre als in der Ideal-Gruppe. Wir können dies sehen, indem wir die Mittelwerte jedes Faktors vergleichen.
Das plotBefehl erzeugt ein Diagramm, das die Beziehung zwischen dem Preis und der Schnittvariablen zeigt. Es ist eine Box-Handlung; Wir haben dieses Diagramm in Abschnitt 16.0.1 behandelt, aber es zeigt im Wesentlichen die Verteilung der Preisvariablen für die beiden von uns analysierten Kürzungsstufen.
Varianzanalyse
Die Varianzanalyse (ANOVA) ist ein statistisches Modell, mit dem die Unterschiede zwischen den Gruppenverteilungen analysiert werden, indem der Mittelwert und die Varianz jeder Gruppe verglichen werden. Das Modell wurde von Ronald Fisher entwickelt. ANOVA bietet einen statistischen Test, ob die Mittelwerte mehrerer Gruppen gleich sind oder nicht, und verallgemeinert den t-Test daher auf mehr als zwei Gruppen.
ANOVAs sind nützlich, um drei oder mehr Gruppen auf statistische Signifikanz zu vergleichen, da die Durchführung mehrerer t-Tests mit zwei Stichproben zu einer erhöhten Wahrscheinlichkeit führen würde, einen statistischen Fehler vom Typ I zu begehen.
Um eine mathematische Erklärung zu erhalten, ist Folgendes erforderlich, um den Test zu verstehen.
x ij = x + (x i - x) + (x ij - x)
Dies führt zu folgendem Modell:
x ij = μ + α i + ∈ ij
Dabei ist μ der Mittelwert und α i der i-te Gruppenmittelwert. Es wird angenommen, dass der Fehlerterm ∈ ij aus einer Normalverteilung stammt. Die Nullhypothese des Tests lautet:
α 1 = α 2 =… = α k
Für die Berechnung der Teststatistik müssen zwei Werte berechnet werden:
- Summe der Quadrate für zwischen Gruppendifferenz -
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- Quadratsummen innerhalb von Gruppen
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^2$$
wobei SSD B einen Freiheitsgrad von k - 1 und SSD W einen Freiheitsgrad von N - k hat. Dann können wir die mittleren quadratischen Differenzen für jede Metrik definieren.
MS B = SSD B / (k - 1)
MS w = SSD w / (N - k)
Schließlich wird die Teststatistik in ANOVA als das Verhältnis der beiden oben genannten Größen definiert
F = MS B / MS w
Dies folgt einer F-Verteilung mit k - 1 und N - k Freiheitsgraden. Wenn die Nullhypothese wahr ist, würde F wahrscheinlich nahe bei 1 liegen. Andernfalls ist das mittlere quadratische MSB zwischen den Gruppen wahrscheinlich groß, was zu einem großen F-Wert führt.
Grundsätzlich untersucht ANOVA die beiden Quellen der Gesamtvarianz und stellt fest, welcher Teil mehr beiträgt. Aus diesem Grund wird es als Varianzanalyse bezeichnet, obwohl die Absicht besteht, Gruppenmittelwerte zu vergleichen.
In Bezug auf die Berechnung der Statistik ist dies in R eigentlich recht einfach. Das folgende Beispiel zeigt, wie es gemacht wird, und zeichnet die Ergebnisse auf.
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')Der Code erzeugt die folgende Ausgabe -

Der p-Wert, den wir im Beispiel erhalten, ist signifikant kleiner als 0,05, daher gibt R das Symbol '***' zurück, um dies zu kennzeichnen. Dies bedeutet, dass wir die Nullhypothese ablehnen und Unterschiede zwischen den mpg-Mitteln zwischen den verschiedenen Gruppen dercyl Variable.
Maschinelles Lernen ist ein Teilgebiet der Informatik, das sich mit Aufgaben wie Mustererkennung, Computer Vision, Spracherkennung und Textanalyse befasst und in engem Zusammenhang mit Statistik und mathematischer Optimierung steht. Zu den Anwendungen gehören unter anderem die Entwicklung von Suchmaschinen, Spamfilterung und optische Zeichenerkennung (OCR). Die Grenzen zwischen Data Mining, Mustererkennung und dem Bereich des statistischen Lernens sind nicht klar und beziehen sich grundsätzlich alle auf ähnliche Probleme.
Maschinelles Lernen kann in zwei Arten von Aufgaben unterteilt werden:
- Überwachtes Lernen
- Unbeaufsichtigtes Lernen
Überwachtes Lernen
Überwachtes Lernen bezieht sich auf eine Art von Problem, bei dem Eingabedaten als Matrix X definiert sind und wir daran interessiert sind, eine Antwort y vorherzusagen . Wo X = {x 1 , x 2 , ..., x n } hat n Prädiktoren und hat zwei Werte y = {c 1 , c 2 } .
Eine Beispielanwendung wäre die Vorhersage der Wahrscheinlichkeit, dass ein Webbenutzer auf Anzeigen klickt, wobei demografische Merkmale als Prädiktoren verwendet werden. Dies wird häufig aufgerufen, um die Klickrate (Click-through-Rate - CTR) vorherzusagen. Dann ist y = {click, not - click} und die Prädiktoren könnten die verwendete IP-Adresse, der Tag, an dem er die Site betreten hat, die Stadt des Benutzers, das Land und andere Funktionen sein, die verfügbar sein könnten.
Unbeaufsichtigtes Lernen
Unbeaufsichtigtes Lernen befasst sich mit dem Problem, Gruppen zu finden, die ineinander ähnlich sind, ohne eine Klasse zu haben, von der man lernen kann. Es gibt verschiedene Ansätze für die Aufgabe, eine Zuordnung von Prädiktoren zu lernen, um Gruppen zu finden, die ähnliche Instanzen in jeder Gruppe gemeinsam haben und sich voneinander unterscheiden.
Eine Beispielanwendung für unbeaufsichtigtes Lernen ist die Kundensegmentierung. In der Telekommunikationsbranche besteht eine häufige Aufgabe beispielsweise darin, Benutzer nach der Nutzung des Telefons zu segmentieren. Dies würde es der Marketingabteilung ermöglichen, jede Gruppe mit einem anderen Produkt anzusprechen.
Naive Bayes ist eine probabilistische Technik zur Konstruktion von Klassifikatoren. Die charakteristische Annahme des naiven Bayes-Klassifikators besteht darin, zu berücksichtigen, dass der Wert eines bestimmten Merkmals angesichts der Klassenvariablen unabhängig vom Wert eines anderen Merkmals ist.
Trotz der zuvor erwähnten vereinfachten Annahmen erzielen naive Bayes-Klassifikatoren in komplexen realen Situationen gute Ergebnisse. Ein Vorteil von naiven Bayes besteht darin, dass nur eine geringe Menge an Trainingsdaten erforderlich ist, um die für die Klassifizierung erforderlichen Parameter abzuschätzen, und dass der Klassifizierer schrittweise trainiert werden kann.
Naive Bayes ist ein bedingtes Wahrscheinlichkeitsmodell: Gegeben ist eine zu klassifizierende Probleminstanz, dargestellt durch einen Vektor x= (x 1 ,…, x n ) repräsentiert einige n Merkmale (unabhängige Variablen) und weist dieser Instanz Wahrscheinlichkeiten für jedes der K möglichen Ergebnisse oder Klassen zu.
$$p(C_k|x_1,....., x_n)$$
Das Problem bei der obigen Formulierung besteht darin, dass es nicht möglich ist, ein solches Modell auf Wahrscheinlichkeitstabellen zu stützen, wenn die Anzahl der Merkmale n groß ist oder wenn ein Merkmal eine große Anzahl von Werten annehmen kann. Wir formulieren das Modell daher neu, um es einfacher zu machen. Unter Verwendung des Bayes-Theorems kann die bedingte Wahrscheinlichkeit wie folgt zerlegt werden:
$$p(C_k|x) = \frac{p(C_k)p(x|C_k)}{p(x)}$$
Dies bedeutet, dass unter den obigen Unabhängigkeitsannahmen die bedingte Verteilung über die Klassenvariable C - beträgt.
$$p(C_k|x_1,....., x_n)\: = \: \frac{1}{Z}p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
wo der Beweis Z = p (x) ist ein Skalierungsfaktor, der nur von x 1 ,…, x n abhängt. Dies ist eine Konstante, wenn die Werte der Merkmalsvariablen bekannt sind. Eine übliche Regel besteht darin, die wahrscheinlichste Hypothese auszuwählen. Dies ist als Maximum a posteriori oder MAP-Entscheidungsregel bekannt. Der entsprechende Klassifikator, ein Bayes-Klassifikator, ist die Funktion, die eine Klassenbezeichnung zuweist$\hat{y} = C_k$ für einige k wie folgt -
$$\hat{y} = argmax\: p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
Das Implementieren des Algorithmus in R ist ein unkomplizierter Prozess. Das folgende Beispiel zeigt, wie ein Naive Bayes-Klassifikator trainiert und zur Vorhersage in einem Spam-Filterproblem verwendet wird.
Das folgende Skript ist in der verfügbar bda/part3/naive_bayes/naive_bayes.R Datei.
# Install these packages
pkgs = c("klaR", "caret", "ElemStatLearn")
install.packages(pkgs)
library('ElemStatLearn')
library("klaR")
library("caret")
# Split the data in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.9))
train = spam[inx,]
test = spam[-inx,]
# Define a matrix with features, X_train
# And a vector with class labels, y_train
X_train = train[,-58]
y_train = train$spam X_test = test[,-58] y_test = test$spam
# Train the model
nb_model = train(X_train, y_train, method = 'nb',
trControl = trainControl(method = 'cv', number = 3))
# Compute
preds = predict(nb_model$finalModel, X_test)$class
tbl = table(y_test, yhat = preds)
sum(diag(tbl)) / sum(tbl)
# 0.7217391Wie wir dem Ergebnis entnehmen können, beträgt die Genauigkeit des Naive Bayes-Modells 72%. Dies bedeutet, dass das Modell 72% der Instanzen korrekt klassifiziert.
k-means Clustering zielt darauf ab, n Beobachtungen in k Cluster zu unterteilen, in denen jede Beobachtung zum Cluster mit dem nächstgelegenen Mittelwert gehört und als Prototyp des Clusters dient. Dies führt zu einer Aufteilung des Datenraums in Voronoi-Zellen.
Bei einer Reihe von Beobachtungen (x 1 , x 2 ,…, x n ) , bei denen jede Beobachtung ein d-dimensionaler reeller Vektor ist, zielt die k-Mittel-Clusterbildung darauf ab, die n Beobachtungen in k Gruppen G = {G 1 , G 2 zu unterteilen ,…, G k } , um die wie folgt definierte Summe von Quadraten (WCSS) innerhalb des Clusters zu minimieren -
$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x - \mu_{i}\parallel ^2$$
Die spätere Formel zeigt die Zielfunktion, die minimiert wird, um die optimalen Prototypen in k-means Clustering zu finden. Die Intuition der Formel ist, dass wir Gruppen finden möchten, die sich voneinander unterscheiden, und dass jedes Mitglied jeder Gruppe mit den anderen Mitgliedern jedes Clusters ähnlich sein sollte.
Das folgende Beispiel zeigt, wie der k-means-Clustering-Algorithmus in R ausgeführt wird.
library(ggplot2)
# Prepare Data
data = mtcars
# We need to scale the data to have zero mean and unit variance
data <- scale(data)
# Determine number of clusters
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:dim(data)[2]) {
wss[i] <- sum(kmeans(data, centers = i)$withinss)
}
# Plot the clusters
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters",
ylab = "Within groups sum of squares")Um einen guten Wert für K zu finden, können wir die Quadratsumme innerhalb der Gruppen für verschiedene Werte von K darstellen. Diese Metrik nimmt normalerweise ab, wenn mehr Gruppen hinzugefügt werden. Wir möchten einen Punkt finden, an dem die Abnahme der Summe innerhalb der Gruppen abnimmt Die Anzahl der Quadrate nimmt langsam ab. In der Darstellung wird dieser Wert am besten durch K = 6 dargestellt.

Nachdem der Wert von K definiert wurde, muss der Algorithmus mit diesem Wert ausgeführt werden.
# K-Means Cluster Analysis
fit <- kmeans(data, 5) # 5 cluster solution
# get cluster means
aggregate(data,by = list(fit$cluster),FUN = mean)
# append cluster assignment
data <- data.frame(data, fit$cluster)Sei I = i 1 , i 2 , ..., i n eine Menge von n binären Attributen, die als Elemente bezeichnet werden. Sei D = t 1 , t 2 , ..., t m eine Menge von Transaktionen, die als Datenbank bezeichnet werden. Jede Transaktion in D hat eine eindeutige Transaktions-ID und enthält eine Teilmenge der Elemente in I. Eine Regel wird als Implikation der Form X ⇒ Y definiert, wobei X, Y ⊆ I und X ∩ Y = ∅.
Die Objektgruppen (für kurze Objektgruppen) X und Y werden als Antezedenz (linke Seite oder LHS) und als Konsequenz (rechte Seite oder RHS) der Regel bezeichnet.
Zur Veranschaulichung der Konzepte verwenden wir ein kleines Beispiel aus dem Supermarktbereich. Die Menge der Elemente ist I = {Milch, Brot, Butter, Bier}. Eine kleine Datenbank mit den Elementen ist in der folgenden Tabelle aufgeführt.
| Transaktions-ID | Artikel |
|---|---|
| 1 | Milchbrot |
| 2 | Brot Butter |
| 3 | Bier |
| 4 | Milch, Brot, Butter |
| 5 | Brot Butter |
Eine Beispielregel für den Supermarkt könnte {Milch, Brot} ⇒ {Butter} sein, was bedeutet, dass Kunden beim Kauf von Milch und Brot auch Butter kaufen. Um interessante Regeln aus dem Satz aller möglichen Regeln auszuwählen, können Einschränkungen für verschiedene Maßstäbe von Bedeutung und Interesse verwendet werden. Die bekanntesten Einschränkungen sind Mindestschwellen für Unterstützung und Vertrauen.
Das Support Supp (X) eines Item-Sets X ist definiert als der Anteil der Transaktionen im Datensatz, die das Item-Set enthalten. In der Beispieldatenbank in Tabelle 1 unterstützt der Item-Set {Milch, Brot} 2/5 = 0,4, da er in 40% aller Transaktionen (2 von 5 Transaktionen) auftritt. Das Auffinden häufiger Objektgruppen kann als Vereinfachung des unbeaufsichtigten Lernproblems angesehen werden.
Das Vertrauen einer Regel ist definiert als conf (X ⇒ Y) = supp (X ∪ Y) / supp (X). Zum Beispiel hat die Regel {Milch, Brot} ⇒ {Butter} ein Vertrauen von 0,2 / 0,4 = 0,5 in die Datenbank in Tabelle 1, was bedeutet, dass für 50% der Transaktionen, die Milch und Brot enthalten, die Regel korrekt ist. Das Vertrauen kann als Schätzung der Wahrscheinlichkeit P (Y | X) interpretiert werden, der Wahrscheinlichkeit, die RHS der Regel in Transaktionen unter der Bedingung zu finden, dass diese Transaktionen auch die LHS enthalten.
In dem Skript in bda/part3/apriori.R den Code zur Implementierung des apriori algorithm kann gefunden werden.
# Load the library for doing association rules
# install.packages(’arules’)
library(arules)
# Data preprocessing
data("AdultUCI")
AdultUCI[1:2,]
AdultUCI[["fnlwgt"]] <- NULL
AdultUCI[["education-num"]] <- NULL
AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),
labels = c("Young", "Middle-aged", "Senior", "Old"))
AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]],
c(0,25,40,60,168)), labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],
c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capitalgain"]]>0]),Inf)),
labels = c("None", "Low", "High"))
AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],
c(-Inf,0, median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capitalloss"]]>0]),Inf)),
labels = c("none", "low", "high"))Um Regeln mit dem Apriori-Algorithmus zu generieren, müssen wir eine Transaktionsmatrix erstellen. Der folgende Code zeigt, wie dies in R gemacht wird.
# Convert the data into a transactions format
Adult <- as(AdultUCI, "transactions")
Adult
# transactions in sparse format with
# 48842 transactions (rows) and
# 115 items (columns)
summary(Adult)
# Plot frequent item-sets
itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)
# generate rules
min_support = 0.01
confidence = 0.6
rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))
rules
inspect(rules[100:110, ])
# lhs rhs support confidence lift
# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486
# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456
# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474
= United-States}Ein Entscheidungsbaum ist ein Algorithmus, der für überwachte Lernprobleme wie Klassifizierung oder Regression verwendet wird. Ein Entscheidungsbaum oder ein Klassifizierungsbaum ist ein Baum, in dem jeder interne (nicht blättrige) Knoten mit einem Eingabe-Feature gekennzeichnet ist. Die Bögen, die von einem mit einem Merkmal gekennzeichneten Knoten kommen, sind mit jedem der möglichen Werte des Merkmals gekennzeichnet. Jedes Blatt des Baumes ist mit einer Klasse oder einer Wahrscheinlichkeitsverteilung über die Klassen gekennzeichnet.
Ein Baum kann "gelernt" werden, indem der Quellensatz basierend auf einem Attributwerttest in Teilmengen aufgeteilt wird. Dieser Vorgang wird für jede abgeleitete Teilmenge rekursiv wiederholtrecursive partitioning. Die Rekursion ist abgeschlossen, wenn die Teilmenge an einem Knoten denselben Wert wie die Zielvariable hat oder wenn die Aufteilung den Vorhersagen keinen Wert mehr hinzufügt. Dieser Prozess der Top-Down-Induktion von Entscheidungsbäumen ist ein Beispiel für einen gierigen Algorithmus und die häufigste Strategie zum Lernen von Entscheidungsbäumen.
Es gibt zwei Haupttypen von Entscheidungsbäumen, die beim Data Mining verwendet werden:
Classification tree - Wenn die Antwort eine nominelle Variable ist, z. B. wenn eine E-Mail Spam ist oder nicht.
Regression tree - wenn das vorhergesagte Ergebnis als reelle Zahl betrachtet werden kann (z. B. das Gehalt eines Arbeitnehmers).
Entscheidungsbäume sind eine einfache Methode und haben daher einige Probleme. Eines dieser Probleme ist die hohe Varianz in den resultierenden Modellen, die Entscheidungsbäume erzeugen. Um dieses Problem zu lösen, wurden Ensemble-Methoden für Entscheidungsbäume entwickelt. Es gibt zwei Gruppen von Ensemble-Methoden, die derzeit ausgiebig verwendet werden -
Bagging decision trees- Diese Bäume werden verwendet, um mehrere Entscheidungsbäume zu erstellen, indem Trainingsdaten wiederholt durch Ersetzen neu abgetastet werden und die Bäume für eine Konsensprognose abgestimmt werden. Dieser Algorithmus wurde als zufällige Gesamtstruktur bezeichnet.
Boosting decision trees- Gradient Boosting kombiniert schwache Lernende; In diesem Fall werden Entscheidungsbäume iterativ zu einem einzigen starken Lernenden. Es passt einen schwachen Baum an die Daten an und passt iterativ schwache Lernende an, um den Fehler des vorherigen Modells zu korrigieren.
# Install the party package
# install.packages('party')
library(party)
library(ggplot2)
head(diamonds)
# We will predict the cut of diamonds using the features available in the
diamonds dataset.
ct = ctree(cut ~ ., data = diamonds)
# plot(ct, main="Conditional Inference Tree")
# Example output
# Response: cut
# Inputs: carat, color, clarity, depth, table, price, x, y, z
# Number of observations: 53940
#
# 1) table <= 57; criterion = 1, statistic = 10131.878
# 2) depth <= 63; criterion = 1, statistic = 8377.279
# 3) table <= 56.4; criterion = 1, statistic = 226.423
# 4) z <= 2.64; criterion = 1, statistic = 70.393
# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48
# 6) color <= E; criterion = 0.997, statistic = 12.829
# 7)* weights = 82
# 6) color > E
#Table of prediction errors
table(predict(ct), diamonds$cut)
# Fair Good Very Good Premium Ideal
# Fair 1388 171 17 0 14
# Good 102 2912 499 26 27
# Very Good 54 998 3334 249 355
# Premium 44 711 5054 11915 1167
# Ideal 22 114 3178 1601 19988
# Estimated class probabilities
probs = predict(ct, newdata = diamonds, type = "prob")
probs = do.call(rbind, probs)
head(probs)Die logistische Regression ist ein Klassifizierungsmodell, bei dem die Antwortvariable kategorisch ist. Es ist ein Algorithmus, der aus Statistiken stammt und für überwachte Klassifizierungsprobleme verwendet wird. Bei der logistischen Regression versuchen wir, den Vektor β der Parameter in der folgenden Gleichung zu finden, die die Kostenfunktion minimieren.
$$logit(p_i) = ln \left ( \frac{p_i}{1 - p_i} \right ) = \beta_0 + \beta_1x_{1,i} + ... + \beta_kx_{k,i}$$
Der folgende Code zeigt, wie ein logistisches Regressionsmodell in R angepasst wird. Wir werden hier den Spam-Datensatz verwenden, um die logistische Regression zu demonstrieren, die auch für Naive Bayes verwendet wurde.
Aus den Vorhersageergebnissen in Bezug auf die Genauigkeit geht hervor, dass das Regressionsmodell im Testsatz eine Genauigkeit von 92,5% erreicht, verglichen mit den 72%, die der Naive Bayes-Klassifikator erreicht.
library(ElemStatLearn)
head(spam)
# Split dataset in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.8))
train = spam[inx,]
test = spam[-inx,]
# Fit regression model
fit = glm(spam ~ ., data = train, family = binomial())
summary(fit)
# Call:
# glm(formula = spam ~ ., family = binomial(), data = train)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -4.5172 -0.2039 0.0000 0.1111 5.4944
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 ***
# A.1 -4.546e-01 2.560e-01 -1.776 0.075720 .
# A.2 -1.630e-01 7.731e-02 -2.108 0.035043 *
# A.3 1.487e-01 1.261e-01 1.179 0.238591
# A.4 2.055e+00 1.467e+00 1.401 0.161153
# A.5 6.165e-01 1.191e-01 5.177 2.25e-07 ***
# A.6 7.156e-01 2.768e-01 2.585 0.009747 **
# A.7 2.606e+00 3.917e-01 6.652 2.88e-11 ***
# A.8 6.750e-01 2.284e-01 2.955 0.003127 **
# A.9 1.197e+00 3.362e-01 3.559 0.000373 ***
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
### Make predictions
preds = predict(fit, test, type = ’response’)
preds = ifelse(preds > 0.5, 1, 0)
tbl = table(target = test$spam, preds)
tbl
# preds
# target 0 1
# email 535 23
# spam 46 316
sum(diag(tbl)) / sum(tbl)
# 0.925Zeitreihen sind eine Folge von Beobachtungen kategorialer oder numerischer Variablen, die durch ein Datum oder einen Zeitstempel indiziert sind. Ein klares Beispiel für Zeitreihendaten ist die Zeitreihe eines Aktienkurses. In der folgenden Tabelle sehen wir die Grundstruktur von Zeitreihendaten. In diesem Fall werden die Beobachtungen stündlich aufgezeichnet.
| Zeitstempel | Standard Preis |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
Normalerweise besteht der erste Schritt bei der Zeitreihenanalyse darin, die Reihen zu zeichnen. Dies erfolgt normalerweise mit einem Liniendiagramm.
Die häufigste Anwendung der Zeitreihenanalyse ist die Vorhersage zukünftiger Werte eines numerischen Werts unter Verwendung der zeitlichen Struktur der Daten. Dies bedeutet, dass die verfügbaren Beobachtungen verwendet werden, um Werte aus der Zukunft vorherzusagen.
Die zeitliche Reihenfolge der Daten impliziert, dass herkömmliche Regressionsmethoden nicht nützlich sind. Um eine robuste Prognose zu erstellen, benötigen wir Modelle, die die zeitliche Reihenfolge der Daten berücksichtigen.
Das am weitesten verbreitete Modell für die Zeitreihenanalyse heißt Autoregressive Moving Average(ARMA). Das Modell besteht aus zwei Teilen, einemautoregressive (AR) Teil und a moving average(MA) Teil. Das Modell wird dann üblicherweise als ARMA (p, q) -Modell bezeichnet, wobei p die Reihenfolge des autoregressiven Teils und q die Reihenfolge des gleitenden Durchschnittsteils ist.
Autoregressives Modell
Der AR (p) wird als autoregressives Modell der Ordnung p gelesen. Mathematisch ist es geschrieben als -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
wobei {φ 1 ,…, φ p } zu schätzende Parameter sind, c eine Konstante ist und die Zufallsvariable ε t das weiße Rauschen darstellt. Für die Werte der Parameter sind einige Einschränkungen erforderlich, damit das Modell stationär bleibt.
Gleitender Durchschnitt
Die Notation MA (q) bezieht sich auf das gleitende Durchschnittsmodell der Ordnung q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
wobei θ 1 , ..., θ q die Parameter des Modells sind, μ die Erwartung von X t ist und ε t , ε t - 1 , ... weiße Rauschfehlerterme sind.
Autoregressiver gleitender Durchschnitt
Das ARMA (p, q) -Modell kombiniert p autoregressive Terme und q gleitende Durchschnittsterme. Mathematisch wird das Modell mit der folgenden Formel ausgedrückt:
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Wir können sehen, dass das ARMA (p, q) -Modell eine Kombination von AR (p) - und MA (q) -Modellen ist.
Um eine gewisse Intuition des Modells zu vermitteln, betrachten Sie, dass der AR-Teil der Gleichung versucht, Parameter für X t - i- Beobachtungen von zu schätzen , um den Wert der Variablen in X t vorherzusagen . Es ist am Ende ein gewichteter Durchschnitt der vergangenen Werte. Der MA-Abschnitt verwendet den gleichen Ansatz, jedoch mit dem Fehler früherer Beobachtungen, ε t - i . Am Ende ist das Ergebnis des Modells also ein gewichteter Durchschnitt.
Das folgende Codefragment zeigt, wie ein ARMA (p, q) in R implementiert wird .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Das Zeichnen der Daten ist normalerweise der erste Schritt, um herauszufinden, ob die Daten eine zeitliche Struktur aufweisen. Wir können der Handlung entnehmen, dass es am Ende eines jeden Jahres starke Spitzen gibt.
Der folgende Code passt ein ARMA-Modell an die Daten an. Es werden mehrere Modellkombinationen ausgeführt und diejenige ausgewählt, die weniger Fehler aufweist.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172In diesem Kapitel werden wir die in Teil 1 des Buches gesammelten Daten verwenden. Die Daten enthalten Text, der Profile von Freiberuflern und den Stundensatz beschreibt, den sie in USD berechnen. Die Idee des folgenden Abschnitts ist es, ein Modell anzupassen, das angesichts der Fähigkeiten eines Freiberuflers in der Lage ist, sein Stundengehalt vorherzusagen.
Der folgende Code zeigt, wie der Rohtext, der in diesem Fall über die Fähigkeiten eines Benutzers verfügt, in eine Wortbeutelmatrix konvertiert wird. Dafür verwenden wir eine R-Bibliothek namens tm. Dies bedeutet, dass wir für jedes Wort im Korpus eine Variable mit der Anzahl der Vorkommen jeder Variablen erstellen.
library(tm)
library(data.table)
source('text_analytics/text_analytics_functions.R')
data = fread('text_analytics/data/profiles.txt')
rate = as.numeric(data$rate)
keep = !is.na(rate)
rate = rate[keep]
### Make bag of words of title and body
X_all = bag_words(data$user_skills[keep])
X_all = removeSparseTerms(X_all, 0.999)
X_all
# <<DocumentTermMatrix (documents: 389, terms: 1422)>>
# Non-/sparse entries: 4057/549101
# Sparsity : 99%
# Maximal term length: 80
# Weighting : term frequency - inverse document frequency (normalized) (tf-idf)
### Make a sparse matrix with all the data
X_all <- as_sparseMatrix(X_all)Nachdem wir den Text als spärliche Matrix dargestellt haben, können wir ein Modell anpassen, das eine spärliche Lösung ergibt. Eine gute Alternative für diesen Fall ist die Verwendung des LASSO (Operator für geringste absolute Schrumpfung und Auswahl). Dies ist ein Regressionsmodell, mit dem die relevantesten Merkmale zur Vorhersage des Ziels ausgewählt werden können.
train_inx = 1:200
X_train = X_all[train_inx, ]
y_train = rate[train_inx]
X_test = X_all[-train_inx, ]
y_test = rate[-train_inx]
# Train a regression model
library(glmnet)
fit <- cv.glmnet(x = X_train, y = y_train,
family = 'gaussian', alpha = 1,
nfolds = 3, type.measure = 'mae')
plot(fit)
# Make predictions
predictions = predict(fit, newx = X_test)
predictions = as.vector(predictions[,1])
head(predictions)
# 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367
# We can compute the mean absolute error for the test data
mean(abs(y_test - predictions))
# 15.02175Jetzt haben wir ein Modell, das mit einer Reihe von Fähigkeiten das Stundengehalt eines Freiberuflers vorhersagen kann. Wenn mehr Daten erfasst werden, verbessert sich die Leistung des Modells, aber der Code zum Implementieren dieser Pipeline ist der gleiche.
Online-Lernen ist ein Teilbereich des maschinellen Lernens, mit dem überwachte Lernmodelle auf umfangreiche Datensätze skaliert werden können. Die Grundidee ist, dass wir nicht alle Daten im Speicher lesen müssen, um zu einem Modell zu passen, sondern nur jede Instanz gleichzeitig lesen müssen.
In diesem Fall zeigen wir, wie ein Online-Lernalgorithmus mithilfe der logistischen Regression implementiert wird. Wie bei den meisten überwachten Lernalgorithmen gibt es eine Kostenfunktion, die minimiert wird. In der logistischen Regression ist die Kostenfunktion definiert als -
$$ J (\ theta) \: = \: \ frac {-1} {m} \ left [\ sum_ {i = 1} ^ {m} y ^ {(i)} log (h _ {\ theta} ( x ^ {(i)})) + (1 - y ^ {(i)}) log (1 - h _ {\ theta} (x ^ {(i)})) \ right] $$
wobei J (& thgr;) die Kostenfunktion darstellt und h & thgr; (x) die Hypothese darstellt. Im Falle einer logistischen Regression wird sie mit der folgenden Formel definiert:
$$ h_ \ theta (x) = \ frac {1} {1 + e ^ {\ theta ^ T x}} $$
Nachdem wir die Kostenfunktion definiert haben, müssen wir einen Algorithmus finden, um sie zu minimieren. Der einfachste Algorithmus, um dies zu erreichen, heißt stochastischer Gradientenabstieg. Die Aktualisierungsregel des Algorithmus für die Gewichte des logistischen Regressionsmodells ist definiert als -
$$ \ theta_j: = \ theta_j - \ alpha (h_ \ theta (x) - y) x $$
Es gibt mehrere Implementierungen des folgenden Algorithmus, aber die in der vowpal wabbit- Bibliothek implementierte ist bei weitem die am weitesten entwickelte. Die Bibliothek ermöglicht das Training von Regressionsmodellen in großem Maßstab und verwendet kleine Mengen an RAM. In den eigenen Worten des Erstellers heißt es: "Das Vowpal Wabbit (VW) -Projekt ist ein schnelles Out-of-Core-Lernsystem, das von Microsoft Research und (zuvor) Yahoo! Research gesponsert wird."
Wir werden mit dem Titanic-Datensatz von a arbeiten kaggleWettbewerb. Die Originaldaten finden Sie in derbda/part3/vwMappe. Hier haben wir zwei Dateien -
- Wir haben Trainingsdaten (train_titanic.csv) und
- unbeschriftete Daten, um neue Vorhersagen zu treffen (test_titanic.csv).
Um das CSV-Format in das zu konvertieren vowpal wabbit Eingabeformat verwenden Sie die csv_to_vowpal_wabbit.pyPython-Skript. Dafür muss natürlich Python installiert sein. Navigieren Sie zubda/part3/vw Ordner, öffnen Sie das Terminal und führen Sie den folgenden Befehl aus:
python csv_to_vowpal_wabbit.pyBeachten Sie, dass Sie in diesem Abschnitt, wenn Sie Windows verwenden, eine Unix-Befehlszeile installieren müssen, die Cygwin- Website dafür aufrufen müssen .
Öffnen Sie das Terminal und auch im Ordner bda/part3/vw und führen Sie den folgenden Befehl aus:
vw train_titanic.vw -f model.vw --binary --passes 20 -c -q ff --sgd --l1
0.00000001 --l2 0.0000001 --learning_rate 0.5 --loss_function logisticLassen Sie uns zusammenfassen, was jedes Argument der vw call meint.
-f model.vw - bedeutet, dass wir das Modell in der Datei model.vw speichern, um später Vorhersagen zu treffen
--binary - Meldet Verlust als binäre Klassifizierung mit -1,1 Bezeichnungen
--passes 20 - Die Daten werden 20 Mal verwendet, um die Gewichte zu lernen
-c - Erstellen Sie eine Cache-Datei
-q ff - Verwenden Sie quadratische Features im f-Namespace
--sgd - Verwenden Sie ein reguläres / klassisches / einfaches stochastisches Gradientenabstiegs-Update, dh nicht adaptiv, nicht normalisiert und nicht invariant.
--l1 --l2 - Regularisierung der Normen L1 und L2
--learning_rate 0.5 - Die Lernrate α ist in der Aktualisierungsregelformel definiert
Der folgende Code zeigt die Ergebnisse der Ausführung des Regressionsmodells in der Befehlszeile. In den Ergebnissen erhalten wir den durchschnittlichen Protokollverlust und einen kleinen Bericht über die Algorithmusleistung.
-loss_function logistic
creating quadratic features for pairs: ff
using l1 regularization = 1e-08
using l2 regularization = 1e-07
final_regressor = model.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 1
power_t = 0.5
decay_learning_rate = 1
using cache_file = train_titanic.vw.cache
ignoring text input in favor of cache input
num sources = 1
average since example example current current current
loss last counter weight label predict features
0.000000 0.000000 1 1.0 -1.0000 -1.0000 57
0.500000 1.000000 2 2.0 1.0000 -1.0000 57
0.250000 0.000000 4 4.0 1.0000 1.0000 57
0.375000 0.500000 8 8.0 -1.0000 -1.0000 73
0.625000 0.875000 16 16.0 -1.0000 1.0000 73
0.468750 0.312500 32 32.0 -1.0000 -1.0000 57
0.468750 0.468750 64 64.0 -1.0000 1.0000 43
0.375000 0.281250 128 128.0 1.0000 -1.0000 43
0.351562 0.328125 256 256.0 1.0000 -1.0000 43
0.359375 0.367188 512 512.0 -1.0000 1.0000 57
0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h
0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h
0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h
0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h
finished run
number of examples per pass = 802
passes used = 11
weighted example sum = 8822
weighted label sum = -2288
average loss = 0.179775 h
best constant = -0.530826
best constant’s loss = 0.659128
total feature number = 427878Jetzt können wir die verwenden model.vw Wir haben trainiert, um Vorhersagen mit neuen Daten zu generieren.
vw -d test_titanic.vw -t -i model.vw -p predictions.txtDie im vorherigen Befehl generierten Vorhersagen werden nicht so normalisiert, dass sie in den Bereich [0, 1] passen. Dazu verwenden wir eine Sigmoid-Transformation.
# Read the predictions
preds = fread('vw/predictions.txt')
# Define the sigmoid function
sigmoid = function(x) {
1 / (1 + exp(-x))
}
probs = sigmoid(preds[[1]])
# Generate class labels
preds = ifelse(probs > 0.5, 1, 0)
head(preds)
# [1] 0 1 0 0 1 0