Big Data Analytics - Diagramme und Grafiken
Der erste Ansatz zur Analyse von Daten besteht darin, sie visuell zu analysieren. Die Ziele dabei sind normalerweise das Finden von Beziehungen zwischen Variablen und univariaten Beschreibungen der Variablen. Wir können diese Strategien wie folgt aufteilen:
- Univariate Analyse
- Multivariate Analyse
Univariate grafische Methoden
Univariateist ein statistischer Begriff. In der Praxis bedeutet dies, dass wir eine Variable unabhängig von den übrigen Daten analysieren möchten. Die Grundstücke, die dies effizient ermöglichen, sind:
Box-Plots
Box-Plots werden normalerweise zum Vergleichen von Verteilungen verwendet. Es ist eine großartige Möglichkeit, visuell zu prüfen, ob es Unterschiede zwischen den Verteilungen gibt. Wir können sehen, ob es Unterschiede zwischen dem Preis von Diamanten für verschiedenen Schliff gibt.
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)Wir können in der Darstellung sehen, dass es Unterschiede in der Verteilung des Diamantenpreises in verschiedenen Schliffarten gibt.

Histogramme
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()Die Ausgabe des obigen Codes lautet wie folgt:
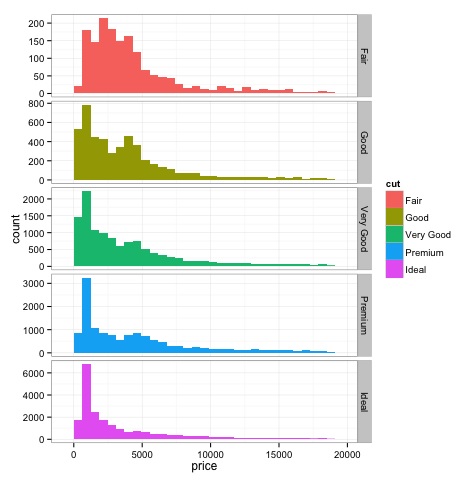
Multivariate grafische Methoden
Multivariate grafische Methoden in der explorativen Datenanalyse haben das Ziel, Beziehungen zwischen verschiedenen Variablen zu finden. Es gibt zwei Möglichkeiten, um dies zu erreichen, die üblicherweise verwendet werden: Zeichnen einer Korrelationsmatrix numerischer Variablen oder einfaches Zeichnen der Rohdaten als Matrix von Streudiagrammen.
Um dies zu demonstrieren, verwenden wir den Diamanten-Datensatz. Öffnen Sie das Skript, um dem Code zu folgenbda/part2/charts/03_multivariate_analysis.R.
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)Der Code erzeugt die folgende Ausgabe -

Dies ist eine Zusammenfassung, die uns sagt, dass es eine starke Korrelation zwischen Preis und Caret gibt und nicht viel zwischen den anderen Variablen.
Eine Korrelationsmatrix kann nützlich sein, wenn wir eine große Anzahl von Variablen haben. In diesem Fall wäre das Zeichnen der Rohdaten nicht praktikabel. Wie bereits erwähnt, können die Rohdaten auch angezeigt werden -
library(GGally)
ggpairs(df)Wir können in der Darstellung sehen, dass die in der Wärmekarte angezeigten Ergebnisse bestätigt sind, es gibt eine Korrelation von 0,922 zwischen den Preis- und Karatvariablen.
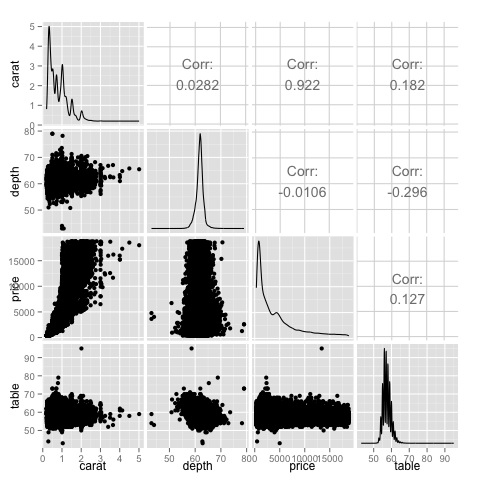
Es ist möglich, diese Beziehung im Preis-Karat-Streudiagramm zu visualisieren, das sich im (3, 1) -Index der Streudiagrammmatrix befindet.