Big Data Analytics - Statistische Methoden

Bei der Analyse von Daten ist ein statistischer Ansatz möglich. Die grundlegenden Werkzeuge, die zur Durchführung der grundlegenden Analyse benötigt werden, sind:

• Korrelationsanalyse
• Varianzanalyse
• Hypothesentest

Bei der Arbeit mit großen Datenmengen ist dies kein Problem, da diese Methoden mit Ausnahme der Korrelationsanalyse nicht rechenintensiv sind. In diesem Fall ist es immer möglich, eine Probe zu entnehmen, und die Ergebnisse sollten robust sein.

Korrelationsanalyse

Die Korrelationsanalyse versucht, lineare Beziehungen zwischen numerischen Variablen zu finden. Dies kann unter verschiedenen Umständen von Nutzen sein. Eine häufige Verwendung ist die explorative Datenanalyse. In Abschnitt 16.0.2 des Buches gibt es ein grundlegendes Beispiel für diesen Ansatz. Zunächst basiert die im genannten Beispiel verwendete Korrelationsmetrik auf derPearson coefficient. Es gibt jedoch eine andere interessante Korrelationsmetrik, die von Ausreißern nicht beeinflusst wird. Diese Metrik wird als Spearman-Korrelation bezeichnet.

Das spearman correlation Die Metrik ist robuster gegenüber Ausreißern als die Pearson-Methode und liefert bessere Schätzungen der linearen Beziehungen zwischen numerischen Variablen, wenn die Daten nicht normal verteilt sind.

library(ggplot2)

# Select variables that are interesting to compare pearson and spearman 
correlation methods. 
x = diamonds[, c('x', 'y', 'z', 'price')]  

# From the histograms we can expect differences in the correlations of both 
metrics.  
# In this case as the variables are clearly not normally distributed, the 
spearman correlation 

# is a better estimate of the linear relation among numeric variables. 
par(mfrow = c(2,2)) 
colnm = names(x) 
for(i in 1:4) { 
   hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i])) 
} 
par(mfrow = c(1,1))

Aus den Histogrammen in der folgenden Abbildung können wir Unterschiede in den Korrelationen beider Metriken erwarten. In diesem Fall ist die Spearman-Korrelation eine bessere Schätzung der linearen Beziehung zwischen numerischen Variablen, da die Variablen eindeutig nicht normalverteilt sind.

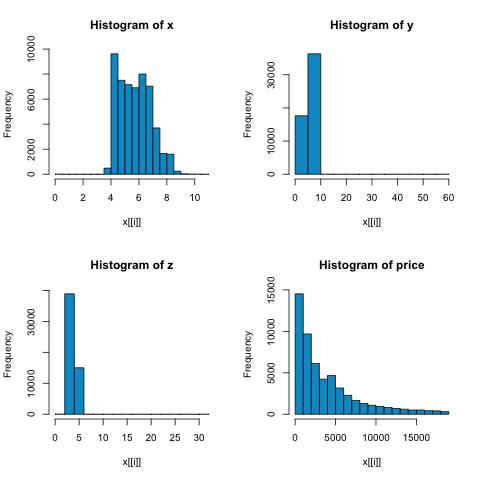
Öffnen Sie die Datei, um die Korrelation in R zu berechnen bda/part2/statistical_methods/correlation/correlation.R das hat diesen Codeabschnitt.

## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson') 
cor_spearman <- cor(x, method = 'spearman')  

### Pearson Correlation 
print(cor_pearson) 
#            x          y          z        price 
# x      1.0000000  0.9747015  0.9707718  0.8844352 
# y      0.9747015  1.0000000  0.9520057  0.8654209 
# z      0.9707718  0.9520057  1.0000000  0.8612494 
# price  0.8844352  0.8654209  0.8612494  1.0000000  

### Spearman Correlation 
print(cor_spearman) 
#              x          y          z      price 
# x      1.0000000  0.9978949  0.9873553  0.9631961 
# y      0.9978949  1.0000000  0.9870675  0.9627188 
# z      0.9873553  0.9870675  1.0000000  0.9572323 
# price  0.9631961  0.9627188  0.9572323  1.0000000

Chi-Quadrat-Test

Mit dem Chi-Quadrat-Test können wir testen, ob zwei Zufallsvariablen unabhängig sind. Dies bedeutet, dass die Wahrscheinlichkeitsverteilung jeder Variablen die andere nicht beeinflusst. Um den Test in R auszuwerten, müssen wir zuerst eine Kontingenztabelle erstellen und dann die Tabelle an die übergebenchisq.test R Funktion.

Lassen Sie uns beispielsweise prüfen, ob zwischen den Variablen: Schnitt und Farbe aus dem Diamanten-Dataset eine Zuordnung besteht. Der Test ist formal definiert als -

• H0: Der variable Schliff und der Diamant sind unabhängig voneinander
• H1: Der variable Schliff und der Diamant sind nicht unabhängig voneinander

Wir würden annehmen, dass es eine Beziehung zwischen diesen beiden Variablen durch ihren Namen gibt, aber der Test kann eine objektive "Regel" geben, die besagt, wie signifikant dieses Ergebnis ist oder nicht.

Im folgenden Codeausschnitt haben wir festgestellt, dass der p-Wert des Tests 2,2e-16 beträgt, dies ist praktisch nahezu Null. Dann nach dem Ausführen des Tests aMonte Carlo simulationfanden wir, dass der p-Wert 0,0004998 ist, was immer noch ziemlich niedriger als der Schwellenwert 0,05 ist. Dieses Ergebnis bedeutet, dass wir die Nullhypothese (H0) ablehnen, also glauben wir den Variablencut und color sind nicht unabhängig.

library(ggplot2)

# Use the table function to compute the contingency table 
tbl = table(diamonds$cut, diamonds$color) 
tbl  

#              D    E    F    G    H    I    J 
# Fair       163  224  312  314  303  175  119 
# Good       662  933  909  871  702  522  307 
# Very Good 1513 2400 2164 2299 1824 1204  678 
# Premium   1603 2337 2331 2924 2360 1428  808 
# Ideal     2834 3903 3826 4884 3115 2093  896  

# In order to run the test we just use the chisq.test function. 
chisq.test(tbl)  

# Pearson’s Chi-squared test 
# data:  tbl 
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation 
# It's needed to add the simulate.p.value = TRUE flag and the amount of 
simulations 
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)  

# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) 
# data:  tbl 
# X-squared = 310.32, df = NA, p-value = 0.0004998

T-Test

Die Idee von t-testist zu bewerten, ob es Unterschiede in einer numerischen Variablenverteilung zwischen verschiedenen Gruppen einer nominalen Variablen gibt. Um dies zu demonstrieren, werde ich die Ebenen der fairen und idealen Ebenen der Faktorvariablen abschneiden und dann die Werte einer numerischen Variablen zwischen diesen beiden Gruppen vergleichen.

data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]

data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the 
cut variable 
df1 = data[, c('cut', 'price')]  

# We can see the price means are different for each group 
tapply(df1$price, df1$cut, mean) 
# Fair    Ideal  
# 4358.758 3457.542

Die t-Tests werden in R mit dem implementiert t.testFunktion. Die Formelschnittstelle zu t.test ist die einfachste Möglichkeit, sie zu verwenden. Die Idee ist, dass eine numerische Variable durch eine Gruppenvariable erklärt wird.

Zum Beispiel: t.test(numeric_variable ~ group_variable, data = data). Im vorherigen Beispiel wurde dienumeric_variable ist price und das group_variable ist cut.

Aus statistischer Sicht testen wir, ob es Unterschiede in der Verteilung der numerischen Variablen zwischen zwei Gruppen gibt. Formal wird der Hypothesentest mit einer Nullhypothese (H0) und einer Alternativhypothese (H1) beschrieben.

• H0: Es gibt keine Unterschiede in der Verteilung der Preisvariablen zwischen den Gruppen Fair und Ideal

• H1 Es gibt Unterschiede in der Verteilung der Preisvariablen zwischen den Gruppen Fair und Ideal

Folgendes kann in R mit dem folgenden Code implementiert werden:

t.test(price ~ cut, data = data)

# Welch Two Sample t-test 
#  
# data:  price by cut 
# t = 9.7484, df = 1894.8, p-value < 2.2e-16 
# alternative hypothesis: true difference in means is not equal to 0 
# 95 percent confidence interval: 
#   719.9065 1082.5251 
# sample estimates: 
#   mean in group Fair mean in group Ideal  
#   4358.758            3457.542   

# Another way to validate the previous results is to just plot the 
distributions using a box-plot 
plot(price ~ cut, data = data, ylim = c(0,12000),  
   col = 'deepskyblue3')

Wir können das Testergebnis analysieren, indem wir prüfen, ob der p-Wert unter 0,05 liegt. In diesem Fall behalten wir die alternative Hypothese bei. Dies bedeutet, dass wir Preisunterschiede zwischen den beiden Stufen des Schnittfaktors festgestellt haben. Bei den Namen der Ebenen hätten wir dieses Ergebnis erwartet, aber wir hätten nicht erwartet, dass der Durchschnittspreis in der Fail-Gruppe höher wäre als in der Ideal-Gruppe. Wir können dies sehen, indem wir die Mittelwerte jedes Faktors vergleichen.

Das plotBefehl erzeugt ein Diagramm, das die Beziehung zwischen dem Preis und der Schnittvariablen zeigt. Es ist eine Box-Handlung; Wir haben dieses Diagramm in Abschnitt 16.0.1 behandelt, aber es zeigt im Wesentlichen die Verteilung der Preisvariablen für die beiden von uns analysierten Kürzungsstufen.

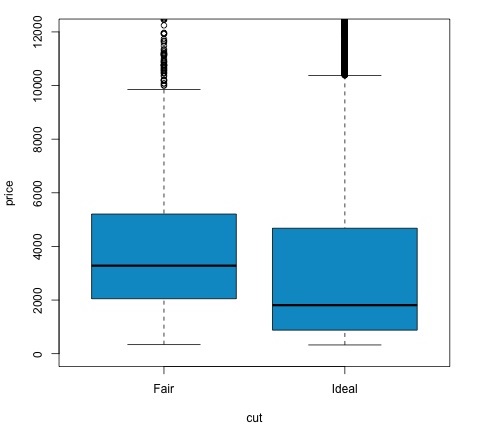
Varianzanalyse

Die Varianzanalyse (ANOVA) ist ein statistisches Modell, mit dem die Unterschiede zwischen den Gruppenverteilungen analysiert werden, indem der Mittelwert und die Varianz jeder Gruppe verglichen werden. Das Modell wurde von Ronald Fisher entwickelt. ANOVA bietet einen statistischen Test, ob die Mittelwerte mehrerer Gruppen gleich sind oder nicht, und verallgemeinert den t-Test daher auf mehr als zwei Gruppen.

ANOVAs sind nützlich, um drei oder mehr Gruppen auf statistische Signifikanz zu vergleichen, da die Durchführung mehrerer T-Tests mit zwei Stichproben zu einer erhöhten Wahrscheinlichkeit führen würde, einen statistischen Fehler vom Typ I zu begehen.

Um eine mathematische Erklärung zu liefern, ist Folgendes erforderlich, um den Test zu verstehen.

x _ij = x + (x _i - x) + (x _ij - x)

Dies führt zu folgendem Modell:

x _ij = μ + α _i + ∈ _ij

Dabei ist μ der Mittelwert und α _i der i-te Gruppenmittelwert. Es wird angenommen, dass der Fehlerterm ∈ _ij aus einer Normalverteilung stammt. Die Nullhypothese des Tests lautet:

α ₁ = α ₂ =… = α _k

Für die Berechnung der Teststatistik müssen zwei Werte berechnet werden:

• Summe der Quadrate für zwischen Gruppendifferenz -

$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$

• Quadratsummen innerhalb von Gruppen

$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$

wobei SSD _B einen Freiheitsgrad von k - 1 und SSD _W einen Freiheitsgrad von N - k hat. Dann können wir die mittleren quadratischen Differenzen für jede Metrik definieren.

MS _B = SSD _B / (k - 1)

MS _w = SSD _w / (N - k)

Schließlich wird die Teststatistik in ANOVA als das Verhältnis der beiden oben genannten Größen definiert

F = MS _B / MS _w

Dies folgt einer F-Verteilung mit k - 1 und N - k Freiheitsgraden. Wenn die Nullhypothese wahr ist, würde F wahrscheinlich nahe bei 1 liegen. Andernfalls ist das mittlere quadratische MSB zwischen den Gruppen wahrscheinlich groß, was zu einem großen F-Wert führt.

Grundsätzlich untersucht ANOVA die beiden Quellen der Gesamtvarianz und sieht, welcher Teil mehr beiträgt. Aus diesem Grund wird es als Varianzanalyse bezeichnet, obwohl die Absicht besteht, Gruppenmittelwerte zu vergleichen.

In Bezug auf die Berechnung der Statistik ist dies in R eigentlich recht einfach. Das folgende Beispiel zeigt, wie es gemacht wird, und zeichnet die Ergebnisse auf.

library(ggplot2)
# We will be using the mtcars dataset 

head(mtcars) 
#                    mpg  cyl disp  hp drat  wt  qsec   vs am  gear carb 
# Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4 
# Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4 
# Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1 
# Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1 
# Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2 
# Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1  

# Let's see if there are differences between the groups of cyl in the mpg variable. 
data = mtcars[, c('mpg', 'cyl')]  
fit = lm(mpg ~ cyl, data = mtcars) 
anova(fit)  

# Analysis of Variance Table 
# Response: mpg 
#           Df Sum Sq Mean Sq F value    Pr(>F)     
# cyl        1 817.71  817.71  79.561 6.113e-10 *** 
# Residuals 30 308.33   10.28 
# Signif. codes:  0 *** 0.001 ** 0.01 * 0.05 . 
# Plot the distribution 
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')

Der Code erzeugt die folgende Ausgabe -

Der p-Wert, den wir im Beispiel erhalten, ist signifikant kleiner als 0,05, daher gibt R das Symbol '***' zurück, um dies zu kennzeichnen. Dies bedeutet, dass wir die Nullhypothese ablehnen und Unterschiede zwischen den mpg-Mitteln zwischen den verschiedenen Gruppen dercyl Variable.