Big Data Analytics - Zeitreihenanalyse

Zeitreihen sind eine Folge von Beobachtungen kategorialer oder numerischer Variablen, die durch ein Datum oder einen Zeitstempel indiziert sind. Ein klares Beispiel für Zeitreihendaten ist die Zeitreihe eines Aktienkurses. In der folgenden Tabelle sehen wir die Grundstruktur von Zeitreihendaten. In diesem Fall werden die Beobachtungen stündlich aufgezeichnet.

Zeitstempel	Standard Preis
2015-10-11 09:00:00	100
2015-10-11 10:00:00	110
2015-10-11 11:00:00	105
2015-10-11 12:00:00	90
2015-10-11 13:00:00	120

Normalerweise besteht der erste Schritt bei der Zeitreihenanalyse darin, die Reihen zu zeichnen. Dies erfolgt normalerweise mit einem Liniendiagramm.

Die häufigste Anwendung der Zeitreihenanalyse ist die Vorhersage zukünftiger Werte eines numerischen Werts unter Verwendung der zeitlichen Struktur der Daten. Dies bedeutet, dass die verfügbaren Beobachtungen verwendet werden, um Werte aus der Zukunft vorherzusagen.

Die zeitliche Reihenfolge der Daten impliziert, dass herkömmliche Regressionsmethoden nicht nützlich sind. Um eine robuste Prognose zu erstellen, benötigen wir Modelle, die die zeitliche Reihenfolge der Daten berücksichtigen.

Das am weitesten verbreitete Modell für die Zeitreihenanalyse heißt Autoregressive Moving Average(ARMA). Das Modell besteht aus zwei Teilen, einemautoregressive (AR) Teil und a moving average(MA) Teil. Das Modell wird dann üblicherweise als ARMA (p, q) -Modell bezeichnet, wobei p die Reihenfolge des autoregressiven Teils und q die Reihenfolge des gleitenden Durchschnittsteils ist.

Autoregressives Modell

Der AR (p) wird als autoregressives Modell der Ordnung p gelesen. Mathematisch ist es geschrieben als -

$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$

wobei {φ ₁ ,…, φ _p } zu schätzende Parameter sind, c eine Konstante ist und die Zufallsvariable ε _t das weiße Rauschen darstellt. Für die Werte der Parameter sind einige Einschränkungen erforderlich, damit das Modell stationär bleibt.

Gleitender Durchschnitt

Die Notation MA (q) bezieht sich auf das gleitende Durchschnittsmodell der Ordnung q -

$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$

wobei θ ₁ , ..., θ _q die Parameter des Modells sind, μ die Erwartung von X _t ist und ε _t , ε _{t - 1} , ... weiße Rauschfehlerterme sind.

Autoregressiver gleitender Durchschnitt

Das ARMA (p, q) -Modell kombiniert p autoregressive Terme und q Terme des gleitenden Durchschnitts. Mathematisch wird das Modell mit der folgenden Formel ausgedrückt:

$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$

Wir können sehen, dass das ARMA (p, q) -Modell eine Kombination von AR (p) - und MA (q) -Modellen ist.

Um eine gewisse Intuition des Modells zu vermitteln, ist zu berücksichtigen, dass der AR-Teil der Gleichung versucht, Parameter für X _{t - i-} Beobachtungen von zu schätzen , um den Wert der Variablen in X _t vorherzusagen . Es ist am Ende ein gewichteter Durchschnitt der vergangenen Werte. Der MA-Abschnitt verwendet den gleichen Ansatz, jedoch mit dem Fehler früherer Beobachtungen, ε _{t - i} . Am Ende ist das Ergebnis des Modells also ein gewichteter Durchschnitt.

Das folgende Codefragment zeigt, wie ein ARMA (p, q) in R implementiert wird .

# install.packages("forecast")
library("forecast")  

# Read the data 
data = scan('fancy.dat') 
ts_data <- ts(data, frequency = 12, start = c(1987,1)) 
ts_data  
plot.ts(ts_data)

Das Zeichnen der Daten ist normalerweise der erste Schritt, um herauszufinden, ob die Daten eine zeitliche Struktur aufweisen. Wir können der Handlung entnehmen, dass es am Ende eines jeden Jahres starke Spitzen gibt.

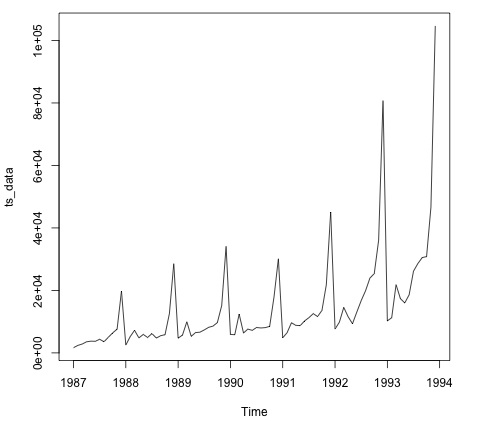
Der folgende Code passt ein ARMA-Modell an die Daten an. Es werden mehrere Modellkombinationen ausgeführt und diejenige ausgewählt, die weniger Fehler aufweist.

# Fit the ARMA model
fit = auto.arima(ts_data) 
summary(fit) 

# Series: ts_data  
# ARIMA(1,1,1)(0,1,1)[12]                     
#    Coefficients: 
#    ar1     ma1    sma1 
# 0.2401  -0.9013  0.7499 
# s.e.  0.1427   0.0709  0.1790 

#  
# sigma^2 estimated as 15464184:  log likelihood = -693.69 
# AIC = 1395.38   AICc = 1395.98   BIC = 1404.43 

# Training set error measures: 
#                 ME        RMSE      MAE        MPE        MAPE      MASE       ACF1 
# Training set   328.301  3615.374  2171.002  -2.481166  15.97302  0.4905797 -0.02521172