Modelar la división de un número entero por una fracción
Aquí, en esta lección, aprendemos cómo usar el modelo de área para dividir un número entero por una fracción. Hay un número entero y una fracción que divide ese número entero. Consideramos un número entero como la cantidad de cuadrados que indica el número. Dividimos cada uno de los cuadrados en la cantidad de partes que indica el denominador de la fracción. Encontramos el resultado de esta división contando el número total de partes de los cuadrados.
Example:
Divida 3 ÷ $ \ frac {1} {2} $ usando un modelo de área.
Solution
Step 1:
El número entero 3 se toma como tres cuadrados. Como la fracción es la mitad, cada uno de los cuadrados se divide en dos mitades.
Step 2:
Ahora se cuentan las mitades en los tres cuadrados y se determina que son 6. Esta es la respuesta que obtenemos al dividir 3 por $ \ frac {1} {2} $ .
Entonces, 3 ÷ $ \ frac {1} {2} $ = 6
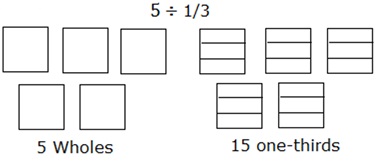
Divida 5 ÷ $ \ frac {1} {3} $ usando un modelo de área.
Solución
Step 1:
La división de 5 en tercios se puede modelar de la siguiente manera:
Considere 5 cuadrados como 5 enteros. Cada uno de los cuadrados se divide a su vez en tres partes o tercios.
Step 2:
Luego, contando el número total de esas partes de los cuadrados o enteros da la respuesta que es 15.
Entonces, 5 ÷ $ \ frac {1} {3} $ = 15
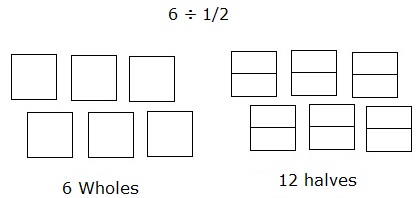
Divida 6 ÷ $ \ frac {1} {2} $ usando un modelo de área.
Solución
Step 1:
La división de 6 en mitades se puede modelar de la siguiente manera:
Considere 6 cuadrados como 6 enteros. Cada uno de los cuadrados se divide en dos partes o mitades.
Step 2:
Luego, contando el número total de esas partes de los cuadrados o enteros da la respuesta que es 12.
Entonces, 6 ÷ $ \ frac {1} {2} $ = 12