Transformation 2D
La transformation signifie changer certains graphiques en quelque chose d'autre en appliquant des règles. Nous pouvons avoir différents types de transformations telles que la translation, la mise à l'échelle vers le haut ou vers le bas, la rotation, le cisaillement, etc. Lorsqu'une transformation a lieu sur un plan 2D, on parle de transformation 2D.
Les transformations jouent un rôle important dans l'infographie pour repositionner les graphiques sur l'écran et modifier leur taille ou leur orientation.
Coordonnées homogènes
Pour effectuer une séquence de transformation telle qu'une translation suivie d'une rotation et d'une mise à l'échelle, nous devons suivre un processus séquentiel -
- Traduisez les coordonnées,
- Faites pivoter les coordonnées traduites, puis
- Mettez à l'échelle les coordonnées pivotées pour terminer la transformation composite.
Pour raccourcir ce processus, nous devons utiliser une matrice de transformation 3 × 3 au lieu d'une matrice de transformation 2 × 2. Pour convertir une matrice 2 × 2 en matrice 3 × 3, nous devons ajouter une coordonnée factice supplémentaire W.
De cette façon, nous pouvons représenter le point par 3 nombres au lieu de 2 nombres, ce qui s'appelle Homogenous Coordinatesystème. Dans ce système, nous pouvons représenter toutes les équations de transformation en multiplication matricielle. Tout point cartésien P (X, Y) peut être converti en coordonnées homogènes par P '(X h , Y h , h).
Traduction
Une traduction déplace un objet vers une position différente sur l'écran. Vous pouvez traduire un point en 2D en ajoutant la coordonnée de translation (t x , t y ) à la coordonnée d'origine (X, Y) pour obtenir la nouvelle coordonnée (X ', Y').
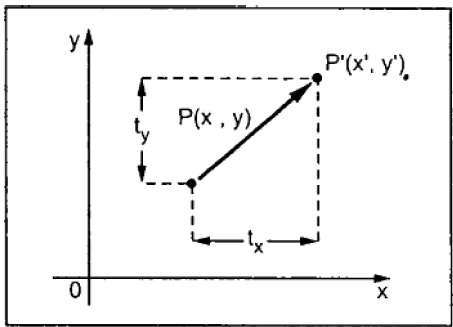
À partir de la figure ci-dessus, vous pouvez écrire que -
X’ = X + tx
Y’ = Y + ty
La paire (t x , t y ) est appelée vecteur de translation ou vecteur de décalage. Les équations ci-dessus peuvent également être représentées à l'aide des vecteurs colonnes.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
Nous pouvons l'écrire comme -
P’ = P + T
Rotation
En rotation, nous faisons pivoter l'objet à un angle particulier θ (thêta) par rapport à son origine. À partir de la figure suivante, nous pouvons voir que le point P (X, Y) est situé à l'angle φ de la coordonnée horizontale X à la distance r de l'origine.
Supposons que vous souhaitiez le faire pivoter à l'angle θ. Après l'avoir fait pivoter vers un nouvel emplacement, vous obtiendrez un nouveau point P '(X', Y ').

En utilisant la trigonométrie standard, la coordonnée d'origine du point P (X, Y) peut être représentée par -
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
De la même manière, nous pouvons représenter le point P '(X', Y ') comme -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $
En remplaçant les équations (1) et (2) respectivement dans (3) et (4), nous obtiendrons
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
Représentant l'équation ci-dessus sous forme matricielle,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OU $$
P '= P. R
Où R est la matrice de rotation
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
L'angle de rotation peut être positif et négatif.
Pour un angle de rotation positif, nous pouvons utiliser la matrice de rotation ci-dessus. Cependant, pour une rotation à angle négatif, la matrice changera comme indiqué ci-dessous -
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ car cos (- \ theta) = cos \ theta \; et \; sin (- \ theta) = −sin \ theta \ right) $$
Mise à l'échelle
Pour modifier la taille d'un objet, la transformation de mise à l'échelle est utilisée. Dans le processus de mise à l'échelle, vous développez ou compressez les dimensions de l'objet. La mise à l'échelle peut être obtenue en multipliant les coordonnées d'origine de l'objet par le facteur de mise à l'échelle pour obtenir le résultat souhaité.
Supposons que les coordonnées d'origine sont (X, Y), les facteurs d'échelle sont (S X , S Y ) et les coordonnées produites sont (X ', Y'). Cela peut être représenté mathématiquement comme indiqué ci-dessous -
X' = X . SX and Y' = Y . SY
Le facteur de mise à l'échelle S X , S Y met à l' échelle l'objet respectivement dans les directions X et Y. Les équations ci-dessus peuvent également être représentées sous forme de matrice comme ci-dessous -
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
OU
P’ = P . S
Où S est la matrice de mise à l'échelle. Le processus de mise à l'échelle est illustré dans la figure suivante.
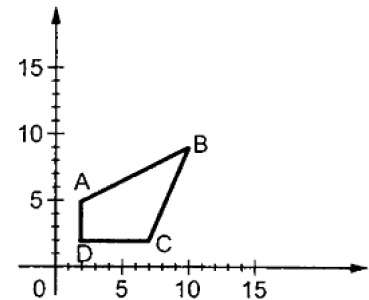
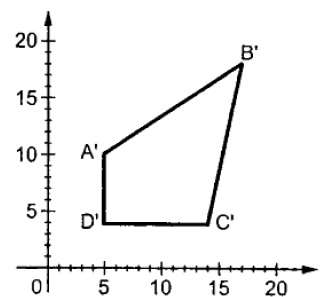
Si nous fournissons des valeurs inférieures à 1 au facteur d'échelle S, nous pouvons réduire la taille de l'objet. Si nous fournissons des valeurs supérieures à 1, nous pouvons augmenter la taille de l'objet.
Réflexion
La réflexion est l'image miroir de l'objet original. En d'autres termes, on peut dire qu'il s'agit d'une opération de rotation à 180 °. Dans la transformation par réflexion, la taille de l'objet ne change pas.
Les figures suivantes montrent des réflexions par rapport aux axes X et Y, et autour de l'origine respectivement.
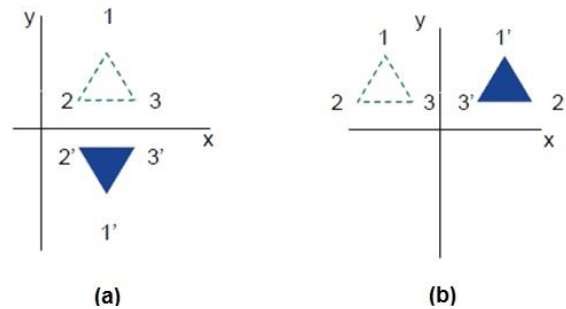
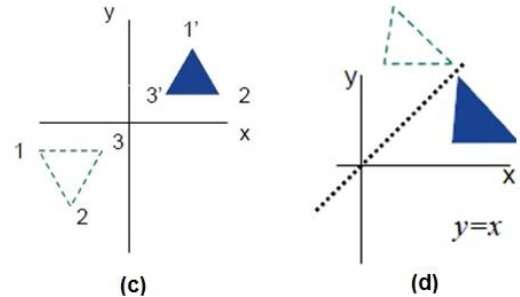
Tondre
Une transformation qui incline la forme d'un objet est appelée transformation de cisaillement. Il y a deux transformations de cisaillementX-Shear et Y-Shear. L'un décale les valeurs des coordonnées X et d'autres décale les valeurs des coordonnées Y. Toutefois; dans les deux cas, une seule coordonnée change ses coordonnées et l'autre préserve ses valeurs. Le cisaillement est également appeléSkewing.
X-Shear
Le X-Shear préserve la coordonnée Y et des modifications sont apportées aux coordonnées X, ce qui entraîne l'inclinaison des lignes verticales vers la droite ou vers la gauche, comme illustré dans la figure ci-dessous.
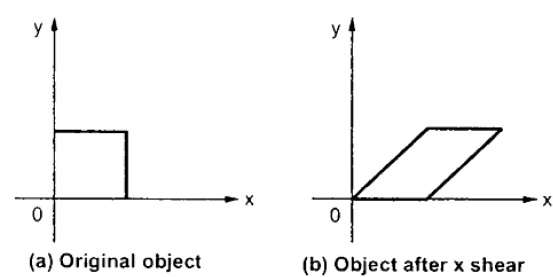
La matrice de transformation pour X-Shear peut être représentée par -
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y-cisaillement
Le cisaillement Y préserve les coordonnées X et modifie les coordonnées Y, ce qui entraîne la transformation des lignes horizontales en lignes inclinées vers le haut ou vers le bas, comme illustré dans la figure suivante.
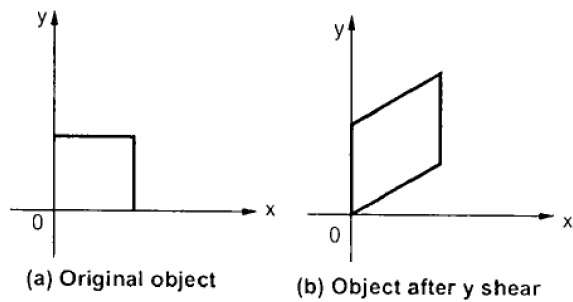
Le cisaillement Y peut être représenté dans une matrice à partir de -
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ timide & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . Oui
Y '= Y
Transformation composite
Si une transformation du plan T1 est suivie d'une seconde transformation plane T2, alors le résultat lui-même peut être représenté par une seule transformation T qui est la composition de T1 et T2 prises dans cet ordre. Cela s'écrit T = T1 ∙ T2.
La transformation composite peut être obtenue par concaténation de matrices de transformation pour obtenir une matrice de transformation combinée.
Une matrice combinée -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
Où [Ti] est une combinaison de
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
Le changement de l'ordre de transformation conduirait à des résultats différents, car en général la multiplication matricielle n'est pas cumulative, c'est-à-dire [A]. [B] ≠ [B]. [A] et l'ordre de multiplication. L'objectif fondamental de la composition des transformations est de gagner en efficacité en appliquant une seule transformation composée à un point, plutôt qu'en appliquant une série de transformations, l'une après l'autre.
Par exemple, pour faire pivoter un objet autour d'un point arbitraire (X p , Y p ), nous devons effectuer trois étapes -
- Traduire le point (X p , Y p ) vers l'origine.
- Faites-le pivoter autour de l'origine.
- Enfin, ramenez le centre de rotation à sa place.