Algorithme de remplissage de polygones
Polygon est une liste ordonnée de sommets, comme illustré dans la figure suivante. Pour remplir des polygones avec des couleurs particulières, vous devez déterminer les pixels tombant sur la bordure du polygone et ceux qui se trouvent à l'intérieur du polygone. Dans ce chapitre, nous verrons comment nous pouvons remplir des polygones en utilisant différentes techniques.

Algorithme de ligne de balayage
Cet algorithme fonctionne en coupant la ligne de balayage avec les arêtes du polygone et remplit le polygone entre les paires d'intersections. Les étapes suivantes décrivent le fonctionnement de cet algorithme.
Step 1 - Découvrez le Ymin et Ymax du polygone donné.
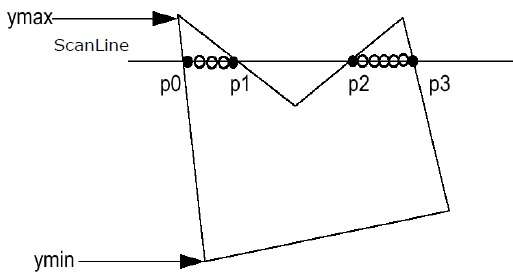
Step 2- ScanLine coupe chaque arête du polygone de Ymin à Ymax. Nommez chaque point d'intersection du polygone. Selon la figure ci-dessus, ils sont nommés p0, p1, p2, p3.
Step 3 - Trier le point d'intersection dans l'ordre croissant de la coordonnée X, c'est-à-dire (p0, p1), (p1, p2) et (p2, p3).
Step 4 - Remplissez toutes ces paires de coordonnées qui sont à l'intérieur des polygones et ignorez les paires alternatives.
Algorithme de remplissage par inondation
Parfois, nous rencontrons un objet dont nous voulons remplir la zone et sa limite avec des couleurs différentes. Nous pouvons peindre de tels objets avec une couleur intérieure spécifiée au lieu de rechercher une couleur de contour particulière comme dans l'algorithme de remplissage de contour.
Au lieu de s'appuyer sur la limite de l'objet, il s'appuie sur la couleur de remplissage. En d'autres termes, il remplace la couleur intérieure de l'objet par la couleur de remplissage. Lorsqu'il n'y a plus de pixels de la couleur intérieure d'origine, l'algorithme est terminé.
Encore une fois, cet algorithme repose sur la méthode Four-connect ou Eight-connect pour remplir les pixels. Mais au lieu de rechercher la couleur de la frontière, il recherche tous les pixels adjacents qui font partie de l'intérieur.
Algorithme de remplissage des limites
L'algorithme de remplissage des limites fonctionne comme son nom. Cet algorithme sélectionne un point à l'intérieur d'un objet et commence à se remplir jusqu'à ce qu'il atteigne la limite de l'objet. La couleur de la limite et la couleur que nous remplissons doivent être différentes pour que cet algorithme fonctionne.
Dans cet algorithme, nous supposons que la couleur de la frontière est la même pour tout l'objet. L'algorithme de remplissage des limites peut être implémenté par 4 pixels connectés ou 8 pixels connectés.
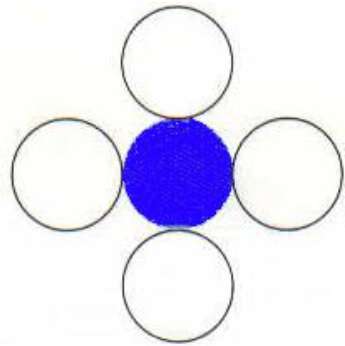
Polygone connecté à 4
Dans cette technique, 4 pixels connectés sont utilisés comme indiqué sur la figure. Nous plaçons les pixels au-dessus, en dessous, à droite et à gauche des pixels actuels et ce processus se poursuivra jusqu'à ce que nous trouvions une limite de couleur différente.
Algorithme
Step 1 - Initialisez la valeur du point de départ (seedx, seedy), fcolor et dcol.
Step 2 - Définissez les valeurs limites du polygone.
Step 3 - Vérifiez si le point de départ actuel est de couleur par défaut, puis répétez les étapes 4 et 5 jusqu'à ce que les pixels limites soient atteints.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - Changez la couleur par défaut avec la couleur de remplissage au point d'origine.
setPixel(seedx, seedy, fcol)Step 5 - Suivez récursivement la procédure avec quatre points de voisinage.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - Sortir
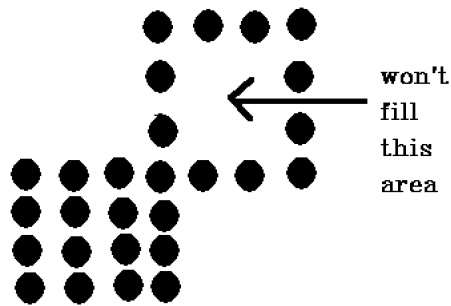
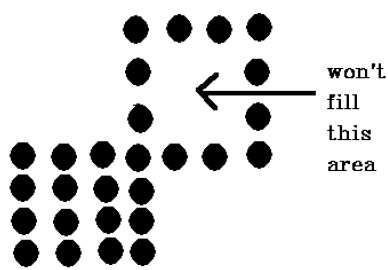
Il y a un problème avec cette technique. Considérez le cas ci-dessous où nous avons essayé de remplir toute la région. Ici, l'image n'est remplie que partiellement. Dans de tels cas, la technique des 4 pixels connectés ne peut pas être utilisée.
Polygone connecté à 8
Dans cette technique, 8 pixels connectés sont utilisés comme indiqué sur la figure. Nous mettons des pixels au-dessus, en dessous, à droite et à gauche des pixels actuels comme nous le faisions dans la technique à 4 connexions.
En plus de cela, nous mettons également les pixels en diagonales afin que toute la zone du pixel actuel soit couverte. Ce processus se poursuivra jusqu'à ce que nous trouvions une limite de couleur différente.

Algorithme
Step 1 - Initialisez la valeur du point de départ (seedx, seedy), fcolor et dcol.
Step 2 - Définissez les valeurs limites du polygone.
Step 3 - Vérifiez si le point de départ actuel est de couleur par défaut puis répétez les étapes 4 et 5 jusqu'à ce que les pixels limites soient atteints
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - Changez la couleur par défaut avec la couleur de remplissage au point d'origine.
setPixel(seedx, seedy, fcol)Step 5 - Suivre récursivement la procédure avec quatre points de voisinage
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - Sortir
La technique à 4 pixels connectés n'a pas réussi à remplir la zone comme indiqué dans la figure suivante, ce qui ne se produira pas avec la technique à 8 connexions.
Test intérieur-extérieur
Cette méthode est également connue sous le nom de counting number method. Lors du remplissage d'un objet, nous avons souvent besoin d'identifier si un point particulier se trouve à l'intérieur ou à l'extérieur de l'objet. Il existe deux méthodes par lesquelles nous pouvons identifier si un point particulier est à l'intérieur ou à l'extérieur d'un objet.
- Règle paire impaire
- Règle de nombre d'enroulement différent de zéro
Règle paire impaire
Dans cette technique, nous compterons le croisement de l'arête le long de la ligne de tout point (x, y) à l'infini. Si le nombre d'interactions est impair, alors le point (x, y) est un point intérieur; et si le nombre d'interactions est pair, alors le point (x, y) est un point extérieur. L'exemple suivant illustre ce concept.
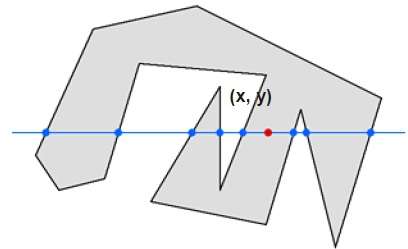
À partir de la figure ci-dessus, nous pouvons voir qu'à partir du point (x, y), le nombre de points d'interactions sur le côté gauche est de 5 et sur le côté droit est de 3. Des deux extrémités, le nombre de points d'interaction est impair, donc le point est considéré dans l'objet.
Règle de nombre d'enroulement différent de zéro
Cette méthode est également utilisée avec les polygones simples pour tester le point donné est intérieur ou non. Il peut être simplement compris à l'aide d'une épingle et d'un élastique. Fixez la goupille sur l'un des bords du polygone et attachez l'élastique à l'intérieur, puis étirez l'élastique le long des bords du polygone.
Lorsque tous les bords du polygone sont couverts par la bande de caoutchouc, vérifiez la broche qui a été fixée au point à tester. Si nous trouvons au moins un vent au point, considérez-le dans le polygone, sinon nous pouvons dire que le point n'est pas à l'intérieur du polygone.
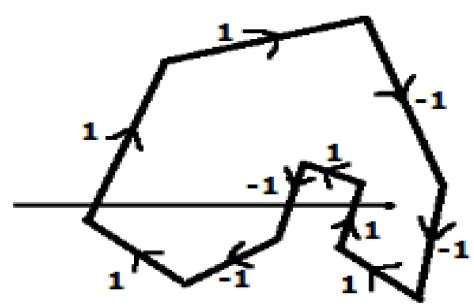
Dans une autre méthode alternative, donnez des directions à toutes les arêtes du polygone. Tracez une ligne de balayage du point à tester vers la plus à gauche de la direction X.
Donnez la valeur 1 à toutes les arêtes qui vont vers le haut et toutes les autres -1 comme valeurs de direction.
Vérifiez les valeurs de direction de bord à partir desquelles la ligne de balayage passe et additionnez-les.
Si la somme totale de cette valeur de direction est non nulle, alors ce point à tester est un interior point, sinon c'est un exterior point.
Dans la figure ci-dessus, nous additionnons les valeurs de direction à partir desquelles la ligne de balayage passe, puis le total est 1 - 1 + 1 = 1; qui est non nul. On dit donc que le point est un point intérieur.