Infographie - Guide rapide

L'infographie est un art de dessiner des images sur des écrans d'ordinateur à l'aide de la programmation. Cela implique des calculs, la création et la manipulation de données. En d'autres termes, on peut dire que l'infographie est un outil de rendu pour la génération et la manipulation d'images.

Tube à rayons cathodiques

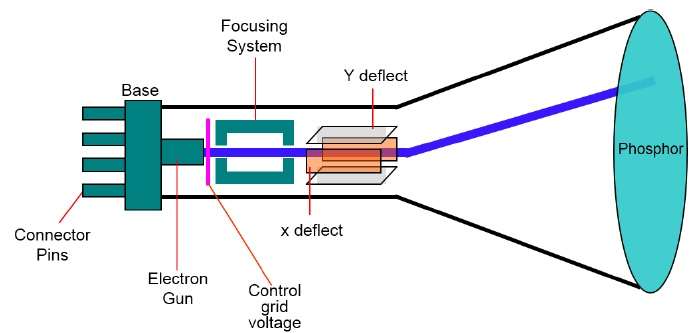
Le périphérique de sortie principal dans un système graphique est le moniteur vidéo. L'élément principal d'un moniteur vidéo est leCathode Ray Tube (CRT), montré dans l'illustration suivante.

Le fonctionnement du CRT est très simple -

Le canon à électrons émet un faisceau d'électrons (rayons cathodiques).
Le faisceau d'électrons passe à travers des systèmes de focalisation et de déviation qui le dirigent vers des positions spécifiées sur l'écran enduit de phosphore.
Lorsque le faisceau frappe l'écran, le luminophore émet une petite tache de lumière à chaque position contactée par le faisceau d'électrons.
Il redessine l'image en dirigeant rapidement le faisceau d'électrons sur les mêmes points d'écran.

Il existe deux manières (Balayage aléatoire et Balayage raster) par lesquelles nous pouvons afficher un objet à l'écran.

Balayage raster

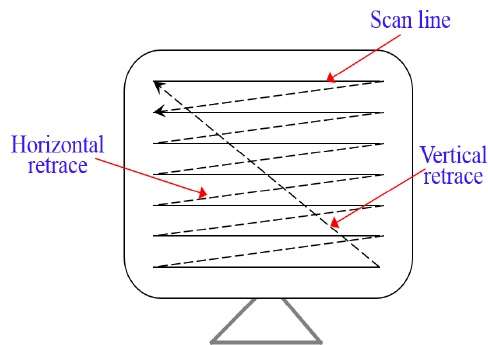
Dans un système de balayage matriciel, le faisceau d'électrons est balayé sur l'écran, une ligne à la fois, de haut en bas. Lorsque le faisceau d'électrons se déplace sur chaque rangée, l'intensité du faisceau est activée et désactivée pour créer un motif de points lumineux.

La définition de l'image est stockée dans la zone de mémoire appelée Refresh Buffer ou Frame Buffer. Cette zone de mémoire contient l'ensemble des valeurs d'intensité pour tous les points de l'écran. Les valeurs d'intensité mémorisées sont ensuite extraites du tampon de rafraîchissement et «peintes» sur l'écran une ligne (ligne de balayage) à la fois, comme illustré dans l'illustration suivante.

Chaque point d'écran est appelé pixel (picture element) ou pel. À la fin de chaque ligne de balayage, le faisceau d'électrons retourne sur le côté gauche de l'écran pour commencer à afficher la ligne de balayage suivante.

Balayage aléatoire (balayage vectoriel)

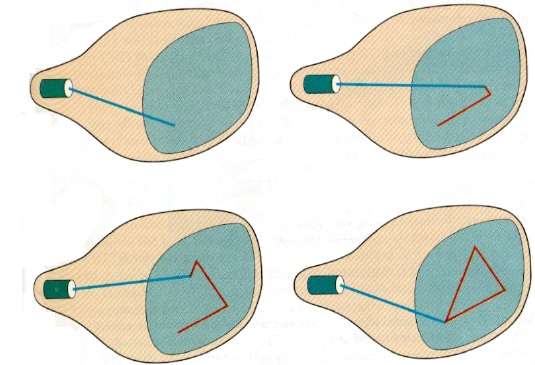
Dans cette technique, le faisceau d'électrons est dirigé uniquement vers la partie de l'écran où l'image doit être dessinée plutôt que de balayer de gauche à droite et de haut en bas comme dans le balayage raster. Il est également appelévector display, stroke-writing display, ou calligraphic display.

La définition d'image est stockée sous la forme d'un ensemble de commandes de dessin au trait dans une zone de mémoire appelée refresh display file. Pour afficher une image spécifiée, le système parcourt l'ensemble des commandes du fichier d'affichage, dessinant chaque ligne de composant à son tour. Une fois toutes les commandes de dessin au trait traitées, le système revient à la première commande de ligne de la liste.

Les affichages à balayage aléatoire sont conçus pour dessiner toutes les lignes de composants d'une image 30 à 60 fois par seconde.

Application de l'infographie

L'infographie a de nombreuses applications, dont certaines sont énumérées ci-dessous -

Computer graphics user interfaces (GUIs) - Un paradigme graphique orienté souris qui permet à l'utilisateur d'interagir avec un ordinateur.
Business presentation graphics - "Une image vaut mille mots".
Cartography - Dessiner des cartes.
Weather Maps - Cartographie en temps réel, représentations symboliques.
Satellite Imaging - Images géodésiques.
Photo Enhancement - Accentuer les photos floues.
Medical imaging - IRM, tomodensitométrie, etc. - Examen interne non invasif.
Engineering drawings - mécanique, électrique, civil, etc. - Remplacement des plans du passé.
Typography - L'utilisation d'images de caractères dans l'édition - remplaçant le type dur du passé.
Architecture - Plans de construction, croquis extérieurs - remplaçant les plans et dessins à la main du passé.
Art - Les ordinateurs constituent un nouveau média pour les artistes.
Training - Simulateurs de vol, instruction assistée par ordinateur, etc.
Entertainment - Films et jeux.
Simulation and modeling - Remplacement de la modélisation physique et des mises en acte

Une ligne relie deux points. C'est un élément de base dans les graphiques. Pour tracer une ligne, vous avez besoin de deux points entre lesquels vous pouvez dessiner une ligne. Dans les trois algorithmes suivants, nous référons le point de ligne comme$X_{0}, Y_{0}$ et le deuxième point de ligne comme $X_{1}, Y_{1}$.

Algorithme DDA

L'algorithme de l'analyseur différentiel numérique (DDA) est l'algorithme de génération de ligne simple qui est expliqué étape par étape ici.

Step 1 - Obtenez l'entrée de deux points finaux $(X_{0}, Y_{0})$ et $(X_{1}, Y_{1})$.

Step 2 - Calculez la différence entre deux extrémités.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3- Sur la base de la différence calculée à l'étape 2, vous devez identifier le nombre d'étapes pour mettre le pixel. Si dx> dy, vous avez besoin de plus d'étapes en coordonnée x; sinon en coordonnée y.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 - Calculez l'incrément en coordonnée x et coordonnée y.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 - Mettez le pixel en incrémentant avec succès les coordonnées x et y en conséquence et terminez le dessin de la ligne.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Génération de ligne de Bresenham

L'algorithme de Bresenham est un autre algorithme de conversion par balayage incrémentiel. Le gros avantage de cet algorithme est qu'il n'utilise que des calculs entiers. Déplacement sur l'axe x par intervalles unitaires et à chaque étape, choisissez entre deux coordonnées y différentes.

Par exemple, comme le montre l'illustration suivante, à partir de la position (2, 3), vous devez choisir entre (3, 3) et (3, 4). Vous souhaitez le point le plus proche de la ligne d'origine.

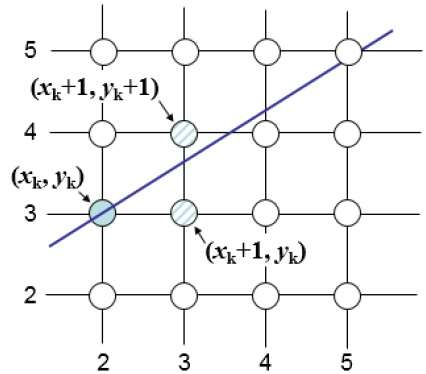
À la position de l'échantillon $X_{k}+1,$ les séparations verticales de la ligne mathématique sont étiquetées comme $d_{upper}$ et $d_{lower}$.

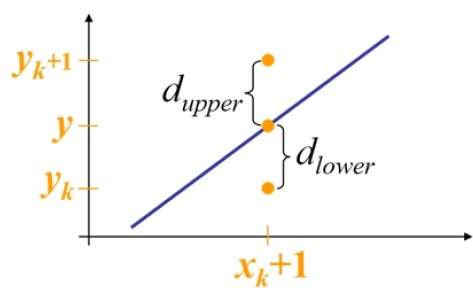
D'après l'illustration ci-dessus, la coordonnée y sur la ligne mathématique à $x_{k}+1$ est -

Y = m ($X_{k}$+1) + b

Alors, $d_{upper}$ et $d_{lower}$ sont donnés comme suit -

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

Vous pouvez les utiliser pour prendre une décision simple sur le pixel le plus proche de la ligne mathématique. Cette décision simple est basée sur la différence entre les deux positions de pixel.

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

Remplaçons m par dy / dx où dx et dy sont les différences entre les extrémités.

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

Donc, un paramètre de décision $P_{k}$car le k ème pas le long d'une ligne est donné par -

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

Le signe du paramètre de décision $P_{k}$ est le même que celui de $d_{lower} - d_{upper}$.

Si $p_{k}$ est négatif, puis choisissez le pixel inférieur, sinon choisissez le pixel supérieur.

N'oubliez pas que les changements de coordonnées se produisent le long de l'axe x par pas d'unités, vous pouvez donc tout faire avec des calculs d'entiers. A l'étape k + 1, le paramètre de décision est donné par -

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

Soustraire $p_{k}$ de cela, nous obtenons -

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

Mais, $x_{k+1}$ est le même que $x_{k+1}$. Alors -

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

Où, $Y_{k+1} – Y_{k}$ vaut 0 ou 1 selon le signe de $P_{k}$.

Le premier paramètre de décision $p_{0}$ est évalué à $(x_{0}, y_{0})$ est donné comme -

$$p_{0} = 2dy - dx$$

Maintenant, en gardant à l'esprit tous les points et calculs ci-dessus, voici l'algorithme de Bresenham pour la pente m <1 -

Step 1 - Entrez les deux extrémités de la ligne, en stockant l'extrémité gauche dans $(x_{0}, y_{0})$.

Step 2 - Tracer le point $(x_{0}, y_{0})$.

Step 3 - Calculez les constantes dx, dy, 2dy et (2dy - 2dx) et obtenez la première valeur du paramètre de décision comme -

$$p_{0} = 2dy - dx$$

Step 4 - À chaque $X_{k}$ le long de la ligne, à partir de k = 0, effectuez le test suivant -

Si $p_{k}$ <0, le point suivant à tracer est $(x_{k}+1, y_{k})$ et

$$p_{k+1} = p_{k} + 2dy$$ Autrement,

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

Step 5 - Répétez l'étape 4 (dx - 1) fois.

Pour m> 1, déterminez si vous devez incrémenter x tout en incrémentant y à chaque fois.

Après résolution, l'équation pour le paramètre de décision $P_{k}$ sera très similaire, seuls les x et y de l'équation sont interchangés.

Algorithme du point médian

L'algorithme du point médian est dû à Bresenham qui a été modifié par Pitteway et Van Aken. Supposons que vous ayez déjà placé le point P à la coordonnée (x, y) et que la pente de la ligne soit 0 ≤ k ≤ 1 comme indiqué dans l'illustration suivante.

Vous devez maintenant décider de placer le point suivant à E ou N. Cela peut être choisi en identifiant le point d'intersection Q le plus proche du point N ou E. Si le point d'intersection Q est le plus proche du point N alors N est considéré comme le point suivant; sinon E.

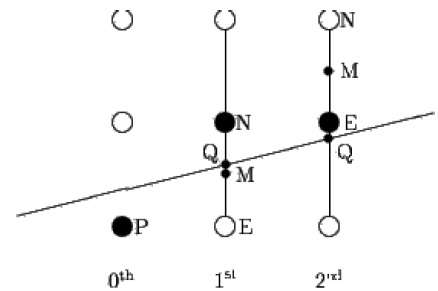
Pour le déterminer, calculez d'abord le point médian M (x + 1, y + ½). Si le point d'intersection Q de la ligne avec la ligne verticale reliant E et N est en dessous de M, alors prenez E comme point suivant; sinon, prenez N comme point suivant.

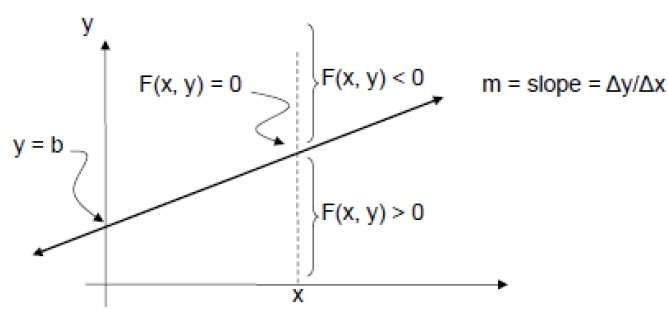
Afin de vérifier cela, nous devons considérer l'équation implicite -

F (x, y) = mx + b - y

Pour m positif à tout X donné,

Si y est sur la ligne, alors F (x, y) = 0
Si y est au-dessus de la ligne, alors F (x, y) <0
Si y est en dessous de la ligne, alors F (x, y)> 0

Dessiner un cercle sur l'écran est un peu complexe que dessiner une ligne. Il existe deux algorithmes populaires pour générer un cercle -Bresenham’s Algorithm et Midpoint Circle Algorithm. Ces algorithmes sont basés sur l'idée de déterminer les points ultérieurs nécessaires pour dessiner le cercle. Laissez-nous discuter des algorithmes en détail -

L'équation du cercle est $X^{2} + Y^{2} = r^{2},$ où r est le rayon.

Algorithme de Bresenham

Nous ne pouvons pas afficher un arc continu sur l'affichage raster. Au lieu de cela, nous devons choisir la position de pixel la plus proche pour terminer l'arc.

Dans l'illustration suivante, vous pouvez voir que nous avons placé le pixel à l'emplacement (X, Y) et que nous devons maintenant décider où placer le pixel suivant - à N (X + 1, Y) ou à S (X + 1, Y-1).

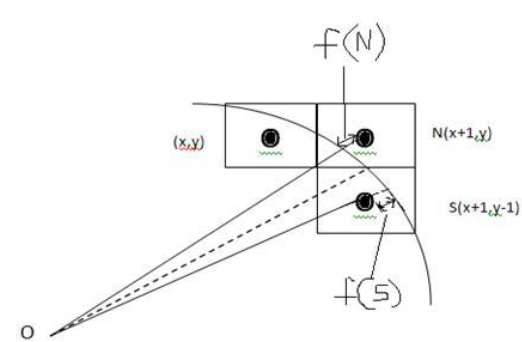
Cela peut être décidé par le paramètre de décision d.

Si d <= 0, alors N (X + 1, Y) doit être choisi comme pixel suivant.
Si d> 0, alors S (X + 1, Y-1) doit être choisi comme pixel suivant.

Algorithme

Step 1- Obtenez les coordonnées du centre du cercle et du rayon, et stockez-les respectivement en x, y et R. Réglez P = 0 et Q = R.

Step 2 - Régler le paramètre de décision D = 3 - 2R.

Step 3 - Répétez jusqu'à l'étape 8 pendant que P ≤ Q.

Step 4 - Appelez Draw Circle (X, Y, P, Q).

Step 5 - Augmentez la valeur de P.

Step 6 - Si D <0 alors D = D + 4P + 6.

Step 7 - Sinon, réglez R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Appelez Draw Circle (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Algorithme du point médian

Step 1 - Rayon d'entrée r et centre du cercle $(x_{c,} y_{c})$ et obtenir le premier point sur la circonférence du cercle centré sur l'origine comme

(x₀, y₀) = (0, r)

Step 2 - Calculer la valeur initiale du paramètre de décision comme

$P_{0}$ = 5/4 - r (Voir la description suivante pour simplifier cette équation.)

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0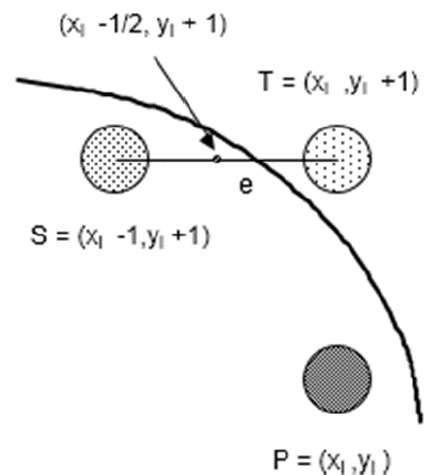

Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

Step 3 - À chaque $X_{K}$ position à partir de K = 0, effectuer le test suivant -

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
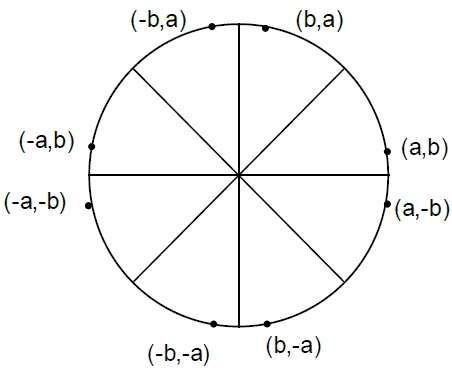
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

Step 4 - Déterminez les points de symétrie dans sept autres octants.

Step 5 - Déplacez chaque position de pixel de calcul (X, Y) sur le chemin circulaire centré sur $(X_{C,} Y_{C})$ et tracez les valeurs de coordonnées.

X = X + X_C,   Y = Y + Y_C

Step 6 - Répétez les étapes 3 à 5 jusqu'à X> = Y.

Polygon est une liste ordonnée de sommets, comme illustré dans la figure suivante. Pour remplir des polygones avec des couleurs particulières, vous devez déterminer les pixels tombant sur la bordure du polygone et ceux qui se trouvent à l'intérieur du polygone. Dans ce chapitre, nous verrons comment nous pouvons remplir des polygones en utilisant différentes techniques.

Algorithme de ligne de balayage

Cet algorithme fonctionne en coupant la ligne de balayage avec les arêtes du polygone et remplit le polygone entre les paires d'intersections. Les étapes suivantes décrivent le fonctionnement de cet algorithme.

Step 1 - Découvrez le Ymin et Ymax du polygone donné.

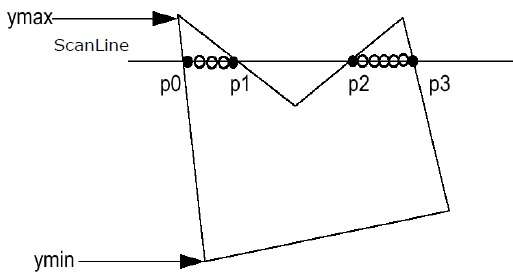
Step 2- ScanLine coupe chaque arête du polygone de Ymin à Ymax. Nommez chaque point d'intersection du polygone. Selon la figure ci-dessus, ils sont nommés p0, p1, p2, p3.

Step 3 - Trier le point d'intersection dans l'ordre croissant des coordonnées X, c'est-à-dire (p0, p1), (p1, p2) et (p2, p3).

Step 4 - Remplissez toutes ces paires de coordonnées qui sont à l'intérieur des polygones et ignorez les paires alternatives.

Algorithme de remplissage par inondation

Parfois, nous rencontrons un objet dont nous voulons remplir la zone et sa limite avec des couleurs différentes. Nous pouvons peindre de tels objets avec une couleur intérieure spécifiée au lieu de rechercher une couleur de contour particulière comme dans l'algorithme de remplissage de contour.

Au lieu de s'appuyer sur la limite de l'objet, il s'appuie sur la couleur de remplissage. En d'autres termes, il remplace la couleur intérieure de l'objet par la couleur de remplissage. Lorsqu'il n'y a plus de pixels de la couleur intérieure d'origine, l'algorithme est terminé.

Encore une fois, cet algorithme repose sur la méthode Four-connect ou Eight-connect pour remplir les pixels. Mais au lieu de rechercher la couleur de la frontière, il recherche tous les pixels adjacents qui font partie de l'intérieur.

Algorithme de remplissage des limites

L'algorithme de remplissage des limites fonctionne comme son nom. Cet algorithme sélectionne un point à l'intérieur d'un objet et commence à se remplir jusqu'à ce qu'il atteigne la limite de l'objet. La couleur de la limite et la couleur que nous remplissons doivent être différentes pour que cet algorithme fonctionne.

Dans cet algorithme, nous supposons que la couleur de la frontière est la même pour tout l'objet. L'algorithme de remplissage des limites peut être implémenté par 4 pixels connectés ou 8 pixels connectés.

Polygone connecté à 4

Dans cette technique, 4 pixels connectés sont utilisés comme indiqué sur la figure. Nous plaçons les pixels au-dessus, en dessous, à droite et à gauche des pixels actuels et ce processus se poursuivra jusqu'à ce que nous trouvions une limite de couleur différente.

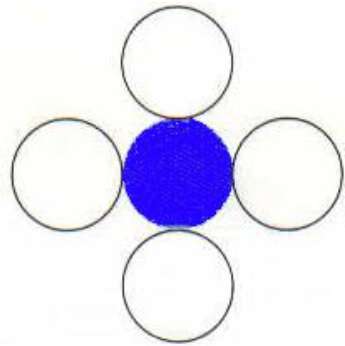
Algorithme

Step 1 - Initialisez la valeur du point de départ (seedx, seedy), fcolor et dcol.

Step 2 - Définissez les valeurs limites du polygone.

Step 3 - Vérifiez si le point de départ actuel est de couleur par défaut, puis répétez les étapes 4 et 5 jusqu'à ce que les pixels limites soient atteints.

If getpixel(x, y) = dcol then repeat step 4 and 5

Step 4 - Changez la couleur par défaut avec la couleur de remplissage au point d'origine.

setPixel(seedx, seedy, fcol)

Step 5 - Suivez récursivement la procédure avec quatre points de voisinage.

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

Step 6 - Sortir

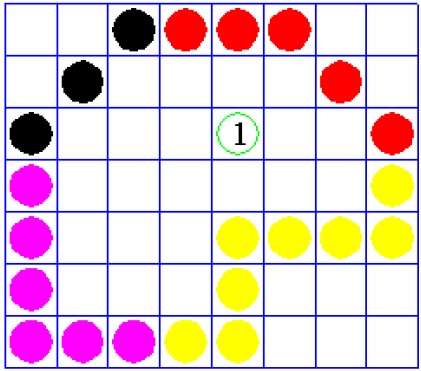
Il y a un problème avec cette technique. Considérez le cas ci-dessous où nous avons essayé de remplir toute la région. Ici, l'image n'est remplie que partiellement. Dans de tels cas, la technique des 4 pixels connectés ne peut pas être utilisée.

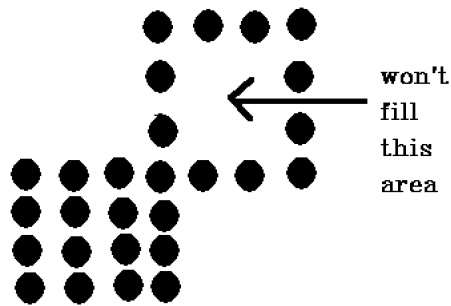
Polygone connecté à 8

Dans cette technique, 8 pixels connectés sont utilisés comme indiqué sur la figure. Nous mettons des pixels au-dessus, en dessous, à droite et à gauche des pixels actuels comme nous le faisions dans la technique à 4 connexions.

En plus de cela, nous mettons également les pixels en diagonales afin que toute la zone du pixel actuel soit couverte. Ce processus se poursuivra jusqu'à ce que nous trouvions une limite de couleur différente.

Algorithme

Step 1 - Initialisez la valeur du point de départ (seedx, seedy), fcolor et dcol.

Step 2 - Définissez les valeurs limites du polygone.

Step 3 - Vérifiez si le point de départ actuel est de couleur par défaut puis répétez les étapes 4 et 5 jusqu'à ce que les pixels limites soient atteints

If getpixel(x,y) = dcol then repeat step 4 and 5

Step 4 - Changez la couleur par défaut avec la couleur de remplissage au point d'origine.

setPixel(seedx, seedy, fcol)

Step 5 - Suivre récursivement la procédure avec quatre points de voisinage

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

Step 6 - Sortir

La technique à 4 pixels connectés n'a pas réussi à remplir la zone indiquée dans la figure suivante, ce qui ne se produira pas avec la technique à 8 connexions.

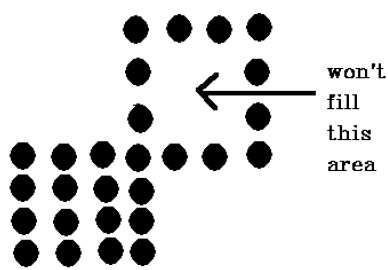
Test intérieur-extérieur

Cette méthode est également connue sous le nom de counting number method. Lors du remplissage d'un objet, nous avons souvent besoin d'identifier si un point particulier se trouve à l'intérieur ou à l'extérieur de l'objet. Il existe deux méthodes par lesquelles nous pouvons identifier si un point particulier est à l'intérieur ou à l'extérieur d'un objet.

Règle paire impaire
Règle de nombre d'enroulement différent de zéro

Règle paire impaire

Dans cette technique, nous comptons le croisement de l'arête le long de la ligne à partir de n'importe quel point (x, y) jusqu'à l'infini. Si le nombre d'interactions est impair, le point (x, y) est un point intérieur. Si le nombre d'interactions est pair, le point (x, y) est un point extérieur. Voici l'exemple pour vous donner une idée claire -

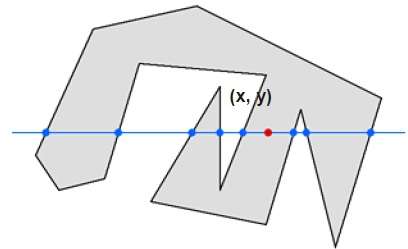
À partir de la figure ci-dessus, nous pouvons voir qu'à partir du point (x, y), le nombre de points d'interactions sur le côté gauche est de 5 et sur le côté droit est de 3. Donc le nombre total de points d'interaction est de 8, ce qui est impair . Par conséquent, le point est considéré dans l'objet.

Règle de nombre d'enroulement différent de zéro

Cette méthode est également utilisée avec les polygones simples pour tester le point donné est intérieur ou non. Il peut être simplement compris à l'aide d'une épingle et d'un élastique. Fixez la goupille sur l'un des bords du polygone et attachez l'élastique à l'intérieur, puis étirez l'élastique le long des bords du polygone.

Lorsque tous les bords du polygone sont couverts par la bande de caoutchouc, vérifiez la broche qui a été fixée au point à tester. Si nous trouvons au moins un vent au point, considérez-le dans le polygone, sinon nous pouvons dire que le point n'est pas à l'intérieur du polygone.

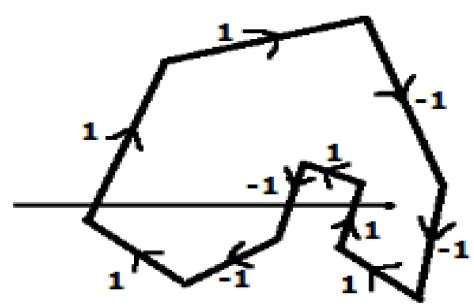
Dans une autre méthode alternative, donnez des directions à toutes les arêtes du polygone. Tracez une ligne de balayage du point à tester vers la plus à gauche de la direction X.

Donnez la valeur 1 à toutes les arêtes qui vont vers le haut et toutes les autres -1 comme valeurs de direction.
Vérifiez les valeurs de direction de bord à partir desquelles la ligne de balayage passe et additionnez-les.
Si la somme totale de cette valeur de direction est non nulle, alors ce point à tester est un interior point, sinon c'est un exterior point.
Dans la figure ci-dessus, nous additionnons les valeurs de direction à partir desquelles la ligne de balayage passe, puis le total est 1 - 1 + 1 = 1; qui est non nul. On dit donc que le point est un point intérieur.

La principale utilisation du détourage en infographie consiste à supprimer des objets, des lignes ou des segments de ligne qui se trouvent en dehors du volet d'affichage. La transformation de visualisation est insensible à la position des points par rapport au volume de visualisation - en particulier les points situés derrière le spectateur - et il est nécessaire de supprimer ces points avant de générer la vue.

Coupure de point

Découper un point d'une fenêtre donnée est très simple. Considérez la figure suivante, où le rectangle indique la fenêtre. L'écrêtage de point nous indique si le point donné (X, Y) est dans la fenêtre donnée ou non; et décide si nous utiliserons les coordonnées minimum et maximum de la fenêtre.

La coordonnée X du point donné est à l'intérieur de la fenêtre, si X se situe entre Wx1 ≤ X ≤ Wx2. De la même manière, la coordonnée Y du point donné est à l'intérieur de la fenêtre, si Y se situe entre Wy1 ≤ Y ≤ Wy2.

Coupure de ligne

Le concept de découpage de ligne est le même que celui de découpage de points. Dans le découpage de ligne, nous allons couper la partie de la ligne qui est à l'extérieur de la fenêtre et ne conserver que la partie qui se trouve à l'intérieur de la fenêtre.

Coupures de la ligne Cohen-Sutherland

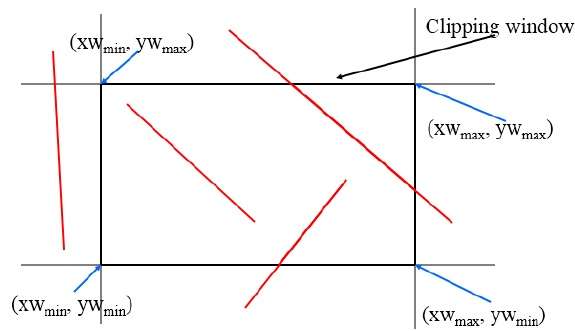
Cet algorithme utilise la fenêtre de découpage comme illustré dans la figure suivante. La coordonnée minimale de la région de découpage est$(XW_{min,} YW_{min})$ et la coordonnée maximale pour la région de découpage est $(XW_{max,} YW_{max})$.

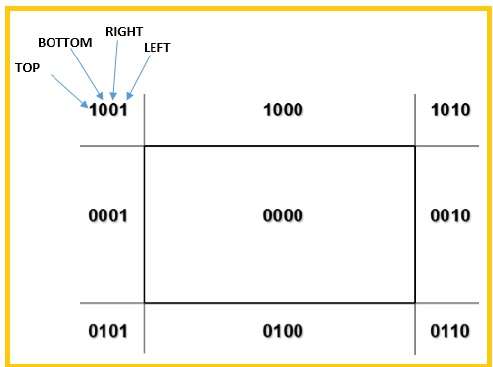
Nous utiliserons 4 bits pour diviser toute la région. Ces 4 bits représentent le haut, le bas, la droite et la gauche de la région, comme illustré dans la figure suivante. Ici leTOP et LEFT bit est mis à 1 car c'est le TOP-LEFT coin.

Il y a 3 possibilités pour la ligne -

La ligne peut être complètement à l'intérieur de la fenêtre (Cette ligne doit être acceptée).
La ligne peut être complètement en dehors de la fenêtre (Cette ligne sera complètement supprimée de la région).
La ligne peut être partiellement à l'intérieur de la fenêtre (nous trouverons le point d'intersection et ne dessinons que la partie de la ligne qui se trouve à l'intérieur de la région).

Algorithme

Step 1 - Attribuez un code de région pour chaque point de terminaison.

Step 2 - Si les deux terminaux ont un code de région 0000 puis acceptez cette ligne.

Step 3 - Sinon, effectuez la logique ANDopération pour les deux codes de région.

Step 3.1 - Si le résultat n'est pas 0000, puis rejetez la ligne.

Step 3.2 - Sinon, vous avez besoin d'écrêtage.

Step 3.2.1 - Choisissez une extrémité de la ligne qui se trouve à l'extérieur de la fenêtre.

Step 3.2.2 - Trouvez le point d'intersection à la limite de la fenêtre (basé sur le code de région).

Step 3.2.3 - Remplacez le point final par le point d'intersection et mettez à jour le code de région.

Step 3.2.4 - Répétez l'étape 2 jusqu'à ce que nous trouvions une ligne tronquée soit trivialement acceptée, soit trivialement rejetée.

Step 4 - Répétez l'étape 1 pour les autres lignes.

Algorithme d'écrêtage de ligne Cyrus-Beck

Cet algorithme est plus efficace que l'algorithme de Cohen-Sutherland. Il utilise une représentation de ligne paramétrique et des produits scalaires simples.

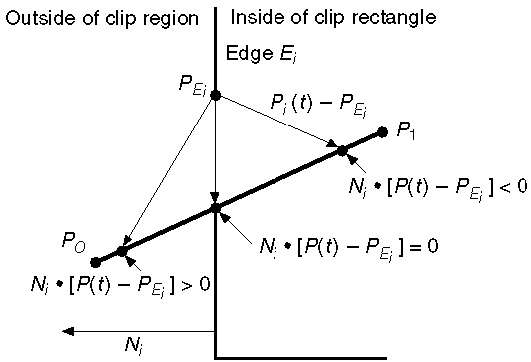
L'équation paramétrique de la ligne est -

P₀P₁:P(t) = P₀ + t(P₁-P₀)

Soit N _i l'arête normale extérieure E _i . Choisissez maintenant n'importe quel point arbitraire P _Ei sur le bord E _i puis le produit scalaire N _i ∙ [P (t) - P _Ei ] détermine si le point P (t) est «à l'intérieur du bord du clip» ou «à l'extérieur» du bord du clip ou «Sur» le bord du clip.

Le point P (t) est à l'intérieur si N _i . [P (t) - P _Ei ] <0

Le point P (t) est extérieur si N _i . [P (t) - P _Ei ]> 0

Le point P (t) est sur l'arête si N _i . [P (t) - P _Ei ] = 0 (point d'intersection)

N _i . [P (t) - P _Ei ] = 0

N _i . [P ₀ + t (P ₁ -P ₀ ) - P _Ei ] = 0 (Remplacement de P (t) par P ₀ + t (P ₁ -P ₀ ))

N _i . [P ₀ - P _Ei ] + N _i .t [P ₁ -P ₀ ] = 0

N _i . [P ₀ - P _Ei ] + N _i ∙ tD = 0 (en remplaçant D par [P ₁ -P ₀ ])

N _i . [P ₀ - P _Ei ] = - N _i ∙ tD

L'équation pour t devient,

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

Il est valable pour les conditions suivantes -

N _i ≠ 0 (l'erreur ne peut pas se produire)
D ≠ 0 (P ₁ ≠ P ₀ )
N _i ∙ D ≠ 0 (P ₀ P ₁ non parallèle à E _i )

Découpage de polygones (algorithme Sutherland Hodgman)

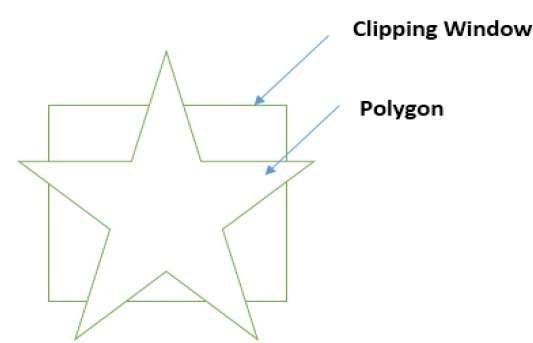
Un polygone peut également être découpé en spécifiant la fenêtre de découpage. L'algorithme de découpage de polygones de Sutherland Hodgeman est utilisé pour le découpage de polygones. Dans cet algorithme, tous les sommets du polygone sont découpés contre chaque bord de la fenêtre de découpage.

Tout d'abord, le polygone est découpé contre le bord gauche de la fenêtre du polygone pour obtenir de nouveaux sommets du polygone. Ces nouveaux sommets sont utilisés pour découper le polygone contre le bord droit, le bord supérieur, le bord inférieur de la fenêtre de découpage, comme illustré dans la figure suivante.

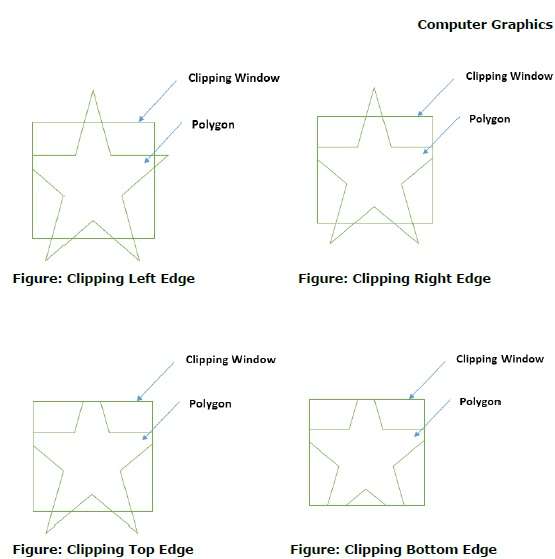
Lors du traitement d'une arête d'un polygone avec fenêtre de découpage, un point d'intersection est trouvé si l'arête n'est pas complètement à l'intérieur de la fenêtre de découpage et si une arête partielle du point d'intersection à l'arête extérieure est découpée. Les figures suivantes montrent des coupures de bord gauche, droit, supérieur et inférieur -

Coupure de texte

Diverses techniques sont utilisées pour fournir un découpage de texte dans une infographie. Cela dépend des méthodes utilisées pour générer des caractères et des exigences d'une application particulière. Il existe trois méthodes de découpage de texte répertoriées ci-dessous:

Coupure de chaîne tout ou rien
Coupure de tout ou aucun caractère
Coupure de texte

La figure suivante montre tout ou aucun découpage de chaîne -

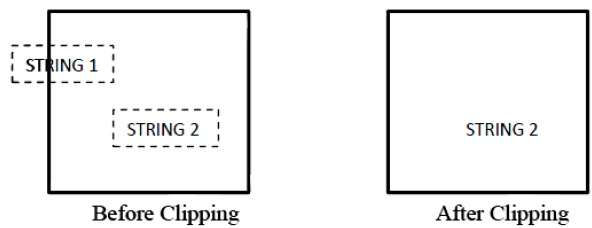
Dans la méthode de découpage de chaîne tout ou rien, soit nous conservons la chaîne entière, soit nous rejetons la chaîne entière en fonction de la fenêtre de découpage. Comme le montre la figure ci-dessus, STRING2 est entièrement à l'intérieur de la fenêtre de découpage donc nous la conservons et STRING1 n'étant que partiellement à l'intérieur de la fenêtre, nous rejetons.

La figure suivante montre tout ou aucun découpage de caractères -

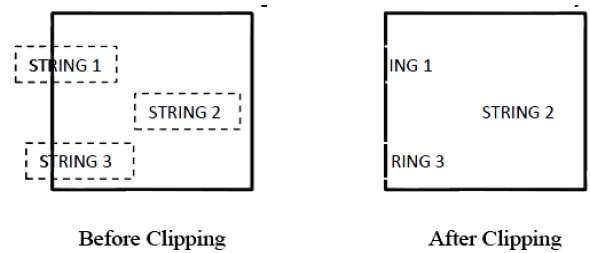
Cette méthode de découpage est basée sur des caractères plutôt que sur une chaîne entière. Dans cette méthode, si la chaîne est entièrement à l'intérieur de la fenêtre de découpage, nous la conservons. Si c'est partiellement à l'extérieur de la fenêtre, alors -

Vous rejetez uniquement la partie de la chaîne étant à l'extérieur
Si le caractère se trouve à la limite de la fenêtre de découpage, nous rejetons ce caractère entier et conservons la chaîne restante.

La figure suivante montre le découpage de texte -

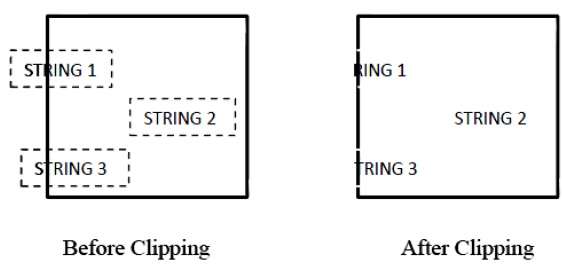
Cette méthode de découpage est basée sur des caractères plutôt que sur la chaîne entière. Dans cette méthode, si la chaîne est entièrement à l'intérieur de la fenêtre de découpage, nous la conservons. Si c'est partiellement à l'extérieur de la fenêtre, alors

Vous rejetez uniquement la partie de la chaîne à l'extérieur.
Si le caractère est à la limite de la fenêtre de découpage, nous ne supprimons que la partie du caractère qui se trouve en dehors de la fenêtre de découpage.

Graphiques Bitmap

Un bitmap est une collection de pixels qui décrit une image. C'est un type d'infographie que l'ordinateur utilise pour stocker et afficher des images. Dans ce type de graphiques, les images sont stockées petit à petit et sont donc appelées graphiques Bit-map. Pour une meilleure compréhension, considérons l'exemple suivant où nous dessinons un visage souriant à l'aide de graphiques bitmap.

Nous allons maintenant voir comment ce smiley est stocké petit à petit en infographie.

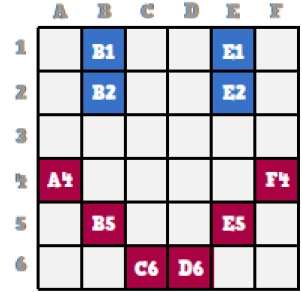
En observant de près le visage souriant d'origine, nous pouvons voir qu'il y a deux lignes bleues qui sont représentées par B1, B2 et E1, E2 dans la figure ci-dessus.

De la même manière, le smiley est représenté en utilisant les bits de combinaison de A4, B5, C6, D6, E5 et F4 respectivement.

Les principaux inconvénients des graphiques bitmap sont:

Nous ne pouvons pas redimensionner l'image bitmap. Si vous essayez de redimensionner, les pixels deviennent flous.
Les bitmaps colorés peuvent être très volumineux.

La transformation signifie changer certains graphiques en quelque chose d'autre en appliquant des règles. Nous pouvons avoir différents types de transformations telles que la translation, la mise à l'échelle vers le haut ou vers le bas, la rotation, le cisaillement, etc. Lorsqu'une transformation a lieu sur un plan 2D, on parle de transformation 2D.

Les transformations jouent un rôle important dans l'infographie pour repositionner les graphiques sur l'écran et modifier leur taille ou leur orientation.

Coordonnées homogènes

Pour effectuer une séquence de transformation telle qu'une translation suivie d'une rotation et d'une mise à l'échelle, nous devons suivre un processus séquentiel -

Traduisez les coordonnées,
Faites pivoter les coordonnées traduites, puis
Mettez à l'échelle les coordonnées pivotées pour terminer la transformation composite.

Pour raccourcir ce processus, nous devons utiliser une matrice de transformation 3 × 3 au lieu d'une matrice de transformation 2 × 2. Pour convertir une matrice 2 × 2 en matrice 3 × 3, nous devons ajouter une coordonnée factice supplémentaire W.

De cette façon, nous pouvons représenter le point par 3 nombres au lieu de 2 nombres, ce qui s'appelle Homogenous Coordinatesystème. Dans ce système, nous pouvons représenter toutes les équations de transformation en multiplication matricielle. Tout point cartésien P (X, Y) peut être converti en coordonnées homogènes par P '(X _h , Y _h , h).

Traduction

Une traduction déplace un objet vers une position différente sur l'écran. Vous pouvez traduire un point en 2D en ajoutant la coordonnée de translation (t _x , t _y ) à la coordonnée d'origine (X, Y) pour obtenir la nouvelle coordonnée (X ', Y').

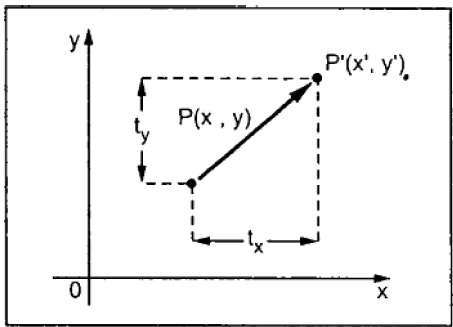
À partir de la figure ci-dessus, vous pouvez écrire que -

X’ = X + t_x

Y’ = Y + t_y

La paire (t _x , t _y ) est appelée vecteur de translation ou vecteur de décalage. Les équations ci-dessus peuvent également être représentées à l'aide des vecteurs colonnes.

$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

Nous pouvons l'écrire comme -

P’ = P + T

Rotation

En rotation, nous faisons pivoter l'objet à un angle particulier θ (thêta) par rapport à son origine. À partir de la figure suivante, nous pouvons voir que le point P (X, Y) est situé à l'angle φ de la coordonnée horizontale X avec la distance r de l'origine.

Supposons que vous vouliez le faire pivoter à l'angle θ. Après l'avoir fait pivoter vers un nouvel emplacement, vous obtiendrez un nouveau point P '(X', Y ').

En utilisant la trigonométrie standard, la coordonnée d'origine du point P (X, Y) peut être représentée par -

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

De la même manière, nous pouvons représenter le point P '(X', Y ') comme -

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

En remplaçant les équations (1) et (2) respectivement dans (3) et (4), nous obtiendrons

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

Représentant l'équation ci-dessus sous forme matricielle,

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P '= P ∙ R

Où R est la matrice de rotation

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

L'angle de rotation peut être positif et négatif.

Pour un angle de rotation positif, nous pouvons utiliser la matrice de rotation ci-dessus. Cependant, pour une rotation à angle négatif, la matrice changera comme indiqué ci-dessous -

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

Mise à l'échelle

Pour modifier la taille d'un objet, une transformation de mise à l'échelle est utilisée. Dans le processus de mise à l'échelle, vous développez ou compressez les dimensions de l'objet. La mise à l'échelle peut être obtenue en multipliant les coordonnées d'origine de l'objet par le facteur de mise à l'échelle pour obtenir le résultat souhaité.

Supposons que les coordonnées d'origine sont (X, Y), les facteurs d'échelle sont (S _X , S _Y ) et les coordonnées produites sont (X ', Y'). Cela peut être représenté mathématiquement comme indiqué ci-dessous -

X' = X . S_X and Y' = Y . S_Y

Le facteur de mise à l'échelle S _X , S _{Y met à l'} échelle l'objet respectivement dans les directions X et Y. Les équations ci-dessus peuvent également être représentées sous forme de matrice comme ci-dessous -

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

P’ = P . S

Où S est la matrice de mise à l'échelle. Le processus de mise à l'échelle est illustré dans la figure suivante.

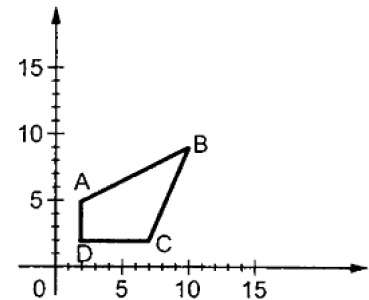
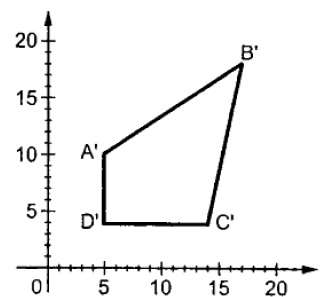
Si nous fournissons des valeurs inférieures à 1 au facteur d'échelle S, nous pouvons réduire la taille de l'objet. Si nous fournissons des valeurs supérieures à 1, nous pouvons augmenter la taille de l'objet.

Réflexion

La réflexion est l'image miroir de l'objet original. En d'autres termes, on peut dire qu'il s'agit d'une opération de rotation à 180 °. Dans la transformation par réflexion, la taille de l'objet ne change pas.

Les figures suivantes montrent des réflexions par rapport aux axes X et Y, et autour de l'origine respectivement.

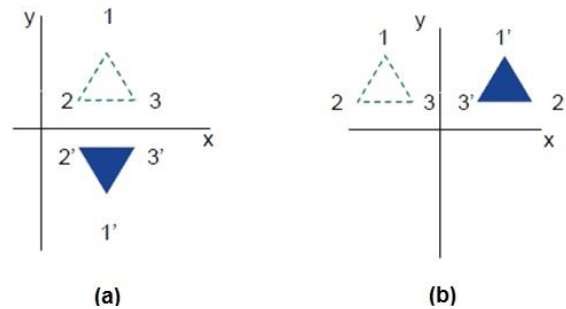
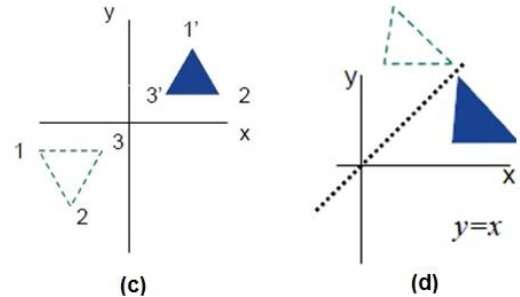
Tondre

Une transformation qui incline la forme d'un objet est appelée transformation de cisaillement. Il y a deux transformations de cisaillementX-Shear et Y-Shear. L'un décale les valeurs des coordonnées X et d'autres décale les valeurs des coordonnées Y. Toutefois; dans les deux cas, une seule coordonnée change ses coordonnées et l'autre préserve ses valeurs. Le cisaillement est également appeléSkewing.

X-Shear

Le X-Shear préserve la coordonnée Y et des modifications sont apportées aux coordonnées X, ce qui entraîne l'inclinaison des lignes verticales vers la droite ou vers la gauche, comme illustré dans la figure ci-dessous.

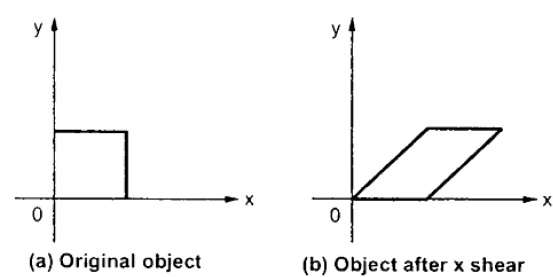
La matrice de transformation pour X-Shear peut être représentée par -

$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

Y '= Y + Sh _y . X

X '= X

Y-cisaillement

Le cisaillement Y préserve les coordonnées X et modifie les coordonnées Y, ce qui entraîne la transformation des lignes horizontales en lignes inclinées vers le haut ou vers le bas, comme illustré dans la figure suivante.

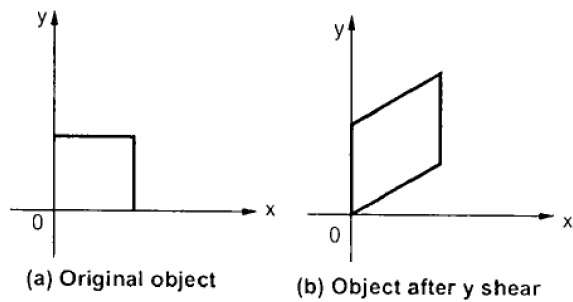
Le cisaillement Y peut être représenté dans une matrice à partir de -

$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

X '= X + Sh _x . Oui

Y '= Y

Transformation composite

Si une transformation du plan T1 est suivie d'une seconde transformation plane T2, alors le résultat lui-même peut être représenté par une seule transformation T qui est la composition de T1 et T2 prises dans cet ordre. Cela s'écrit T = T1 ∙ T2.

La transformation composite peut être obtenue par concaténation de matrices de transformation pour obtenir une matrice de transformation combinée.

Une matrice combinée -

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

Où [Ti] est une combinaison de

Translation
Scaling
Shearing
Rotation
Reflection

Le changement de l'ordre de transformation conduirait à des résultats différents, car en général la multiplication matricielle n'est pas cumulative, c'est-à-dire [A]. [B] ≠ [B]. [A] et l'ordre de multiplication. L'objectif fondamental de la composition des transformations est de gagner en efficacité en appliquant une seule transformation composée à un point, plutôt qu'en appliquant une série de transformations, l'une après l'autre.

Par exemple, pour faire pivoter un objet autour d'un point arbitraire (X _p , Y _p ), nous devons effectuer trois étapes -

Traduire le point (X _p , Y _p ) vers l'origine.
Faites-le pivoter autour de l'origine.
Enfin, ramenez le centre de rotation à sa place.

Dans le système 2D, nous n'utilisons que deux coordonnées X et Y mais en 3D, une coordonnée Z supplémentaire est ajoutée. Les techniques graphiques 3D et leur application sont fondamentales pour les industries du divertissement, des jeux et de la conception assistée par ordinateur. C'est un domaine de recherche continu en visualisation scientifique.

En outre, les composants graphiques 3D font désormais partie de presque tous les ordinateurs personnels et, bien que traditionnellement destinés aux logiciels à forte intensité graphique tels que les jeux, ils sont de plus en plus utilisés par d'autres applications.

Projection parallèle

La projection parallèle supprime la coordonnée z et les lignes parallèles de chaque sommet de l'objet sont étendues jusqu'à ce qu'elles coupent le plan de vue. En projection parallèle, nous spécifions une direction de projection au lieu d'un centre de projection.

En projection parallèle, la distance entre le centre de projection et le plan du projet est infinie. Dans ce type de projection, nous connectons les sommets projetés par des segments de ligne qui correspondent à des connexions sur l'objet d'origine.

Les projections parallèles sont moins réalistes, mais elles sont bonnes pour des mesures exactes. Dans ce type de projections, les lignes parallèles restent parallèles et les angles ne sont pas conservés. Différents types de projections parallèles sont présentés dans la hiérarchie suivante.

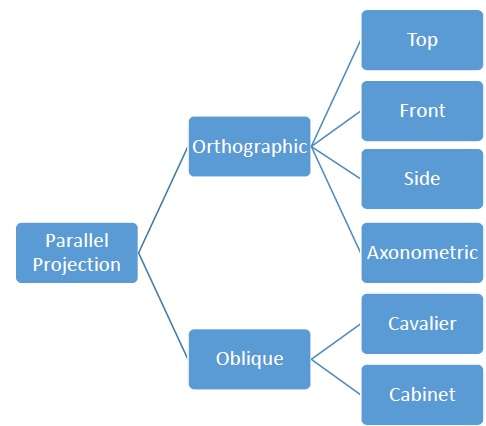
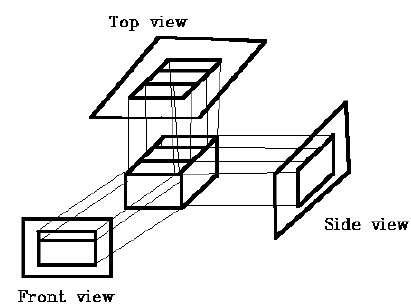
Projection orthographique

En projection orthographique, la direction de projection est normale à la projection du plan. Il existe trois types de projections orthographiques -

Projection avant
Projection supérieure
Projection latérale

Projection oblique

En projection oblique, la direction de projection n'est pas normale à la projection du plan. En projection oblique, nous pouvons mieux voir l'objet que la projection orthographique.

Il existe deux types de projections obliques - Cavalier et Cabinet. La projection Cavalier fait un angle de 45 ° avec le plan de projection. La projection d'une ligne perpendiculaire au plan de vue a la même longueur que la ligne elle-même dans la projection Cavalier. Dans une projection cavalière, les facteurs de raccourcissement pour les trois directions principales sont égaux.

La projection Cabinet fait un angle de 63,4 ° avec le plan de projection. Dans la projection Cabinet, les lignes perpendiculaires à la surface de visualisation sont projetées à la moitié de leur longueur réelle. Les deux projections sont illustrées dans la figure suivante -

Projections isométriques

Les projections orthographiques qui montrent plus d'un côté d'un objet sont appelées axonometric orthographic projections. La projection axonométrique la plus courante est uneisometric projectionoù le plan de projection coupe chaque axe de coordonnées dans le système de coordonnées du modèle à une distance égale. Dans cette projection, le parallélisme des lignes est conservé mais les angles ne sont pas conservés. La figure suivante montre une projection isométrique -

Projection en perspective

En projection en perspective, la distance entre le centre de projection et le plan du projet est finie et la taille de l'objet varie inversement avec la distance, ce qui semble plus réaliste.

La distance et les angles ne sont pas conservés et les lignes parallèles ne restent pas parallèles. Au lieu de cela, ils convergent tous en un seul point appelécenter of projection ou projection reference point. Il existe 3 types de projections en perspective qui sont illustrés dans le tableau suivant.

One point la projection en perspective est simple à dessiner.
Two point la projection en perspective donne une meilleure impression de profondeur.
Three point la projection en perspective est la plus difficile à dessiner.

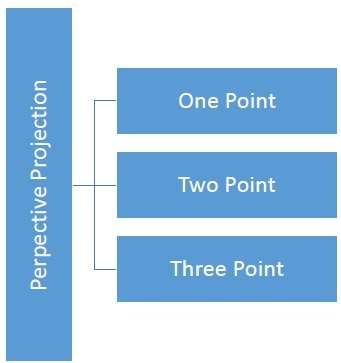
La figure suivante montre les trois types de projection en perspective -

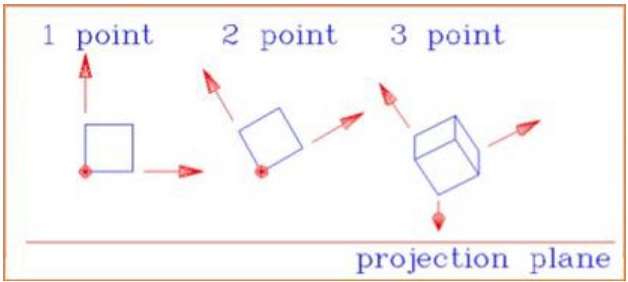
Traduction

En translation 3D, nous transférons la coordonnée Z avec les coordonnées X et Y. Le processus de traduction en 3D est similaire à la traduction 2D. Une traduction déplace un objet dans une position différente sur l'écran.

La figure suivante montre l'effet de la translation -

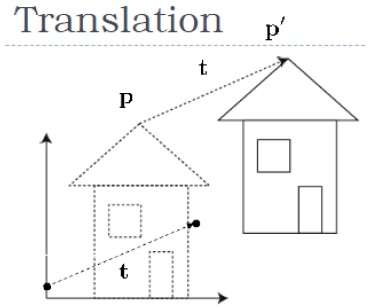
Un point peut être traduit en 3D en ajoutant des coordonnées de translation $(t_{x,} t_{y,} t_{z})$ à la coordonnée d'origine (X, Y, Z) pour obtenir la nouvelle coordonnée (X ', Y', Z ').

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P '= P ∙ T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

Rotation

La rotation 3D est différente de la rotation 2D. En rotation 3D, nous devons spécifier l'angle de rotation avec l'axe de rotation. Nous pouvons effectuer une rotation 3D autour des axes X, Y et Z. Ils sont représentés sous forme de matrice comme ci-dessous -

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

La figure suivante explique la rotation autour de différents axes -

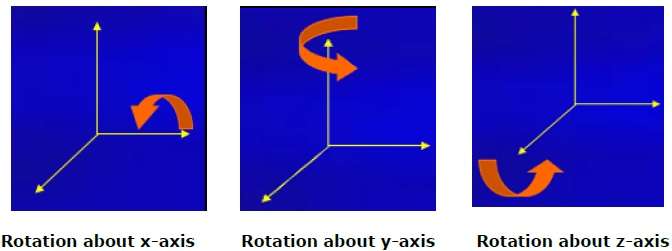
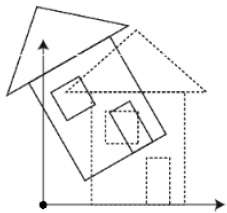
Mise à l'échelle

Vous pouvez modifier la taille d'un objet à l'aide de la transformation de mise à l'échelle. Dans le processus de mise à l'échelle, vous développez ou compressez les dimensions de l'objet. La mise à l'échelle peut être obtenue en multipliant les coordonnées d'origine de l'objet par le facteur de mise à l'échelle pour obtenir le résultat souhaité. La figure suivante montre l'effet de la mise à l'échelle 3D -

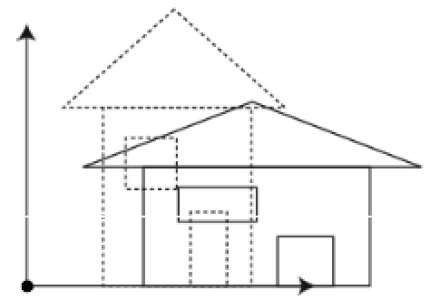
Dans l'opération de mise à l'échelle 3D, trois coordonnées sont utilisées. Supposons que les coordonnées d'origine sont (X, Y, Z), les facteurs d'échelle sont$(S_{X,} S_{Y,} S_{z})$respectivement, et les coordonnées produites sont (X ', Y', Z '). Cela peut être représenté mathématiquement comme indiqué ci-dessous -

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P '= P ∙ S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

Tondre

Une transformation qui incline la forme d'un objet est appelée le shear transformation. Comme dans le cisaillement 2D, nous pouvons cisailler un objet le long de l'axe X, Y ou Z en 3D.

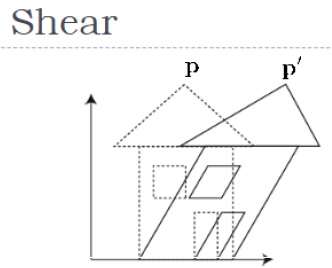
Comme le montre la figure ci-dessus, il y a une coordonnée P. Vous pouvez la cisailler pour obtenir une nouvelle coordonnée P ', qui peut être représentée sous forme de matrice 3D comme ci-dessous -

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P '= P ∙ Sh

$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$

$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$

$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$

Matrices de transformation

La matrice de transformation est un outil de base pour la transformation. Une matrice de dimensions nxm est multipliée par la coordonnée des objets. Habituellement, des matrices 3 x 3 ou 4 x 4 sont utilisées pour la transformation. Par exemple, considérez la matrice suivante pour diverses opérations.

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Translation Matrix	Scaling Matrix	Shear Matrix
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Rotation Matrix

En infographie, nous avons souvent besoin de dessiner différents types d'objets sur l'écran. Les objets ne sont pas toujours plats et nous devons dessiner des courbes plusieurs fois pour dessiner un objet.

Types de courbes

Une courbe est un ensemble infiniment grand de points. Chaque point a deux voisins à l'exception des points d'extrémité. Les courbes peuvent être globalement classées en trois catégories -explicit, implicit, et parametric curves.

Courbes implicites

Les représentations de courbes implicites définissent l'ensemble de points sur une courbe en utilisant une procédure qui permet de tester pour voir si un point se trouve sur la courbe. Habituellement, une courbe implicite est définie par une fonction implicite de la forme -

f (x, y) = 0

Il peut représenter des courbes à plusieurs valeurs (plusieurs valeurs y pour une valeur x). Un exemple courant est le cercle, dont la représentation implicite est

x² + y² - R² = 0

Courbes explicites

Une fonction mathématique y = f (x) peut être représentée sous forme de courbe. Une telle fonction est la représentation explicite de la courbe. La représentation explicite n'est pas générale, car elle ne peut pas représenter des lignes verticales et est également à valeur unique. Pour chaque valeur de x, une seule valeur de y est normalement calculée par la fonction.

Courbes paramétriques

Les courbes de forme paramétrique sont appelées courbes paramétriques. Les représentations de courbes explicites et implicites ne peuvent être utilisées que lorsque la fonction est connue. En pratique, les courbes paramétriques sont utilisées. Une courbe paramétrique bidimensionnelle a la forme suivante -

P (t) = f (t), g (t) ou P (t) = x (t), y (t)

Les fonctions f et g deviennent les coordonnées (x, y) de n'importe quel point de la courbe, et les points sont obtenus lorsque le paramètre t varie sur un certain intervalle [a, b], normalement [0, 1].

Courbes de Bézier

La courbe de Bézier est découverte par l'ingénieur français Pierre Bézier. Ces courbes peuvent être générées sous le contrôle d'autres points. Des tangentes approximatives à l'aide de points de contrôle sont utilisées pour générer une courbe. La courbe de Bézier peut être représentée mathématiquement par -

$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$

Où $p_{i}$ est l'ensemble des points et ${B_{i}^{n}}(t)$ représente les polynômes de Bernstein qui sont donnés par -

$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$

Où n est le degré polynomial, i est l'indice, et t est la variable.

La courbe de Bézier la plus simple est la ligne droite à partir du point $P_{0}$ à $P_{1}$. Une courbe de Bézier quadratique est déterminée par trois points de contrôle. Une courbe de Bézier cubique est déterminée par quatre points de contrôle.

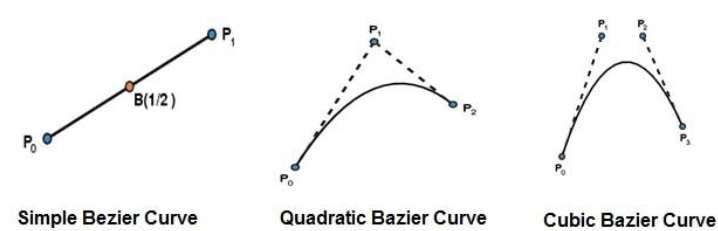
Propriétés des courbes de Bézier

Les courbes de Bézier ont les propriétés suivantes -

Ils suivent généralement la forme du polygone de contrôle, qui se compose des segments joignant les points de contrôle.
Ils passent toujours par les premier et dernier points de contrôle.
Ils sont contenus dans la coque convexe de leurs points de contrôle définissant.
Le degré du polynôme définissant le segment de courbe est un de moins que le nombre de points de polygone de définition. Par conséquent, pour 4 points de contrôle, le degré du polynôme est 3, c'est-à-dire un polynôme cubique.
Une courbe de Bézier suit généralement la forme du polygone de définition.
La direction du vecteur tangent aux extrémités est la même que celle du vecteur déterminé par le premier et le dernier segments.
La propriété de coque convexe pour une courbe de Bézier garantit que le polynôme suit en douceur les points de contrôle.
Aucune ligne droite ne coupe une courbe de Bézier plus de fois qu'elle ne croise son polygone de contrôle.
Ils sont invariants sous une transformation affine.
Les courbes de Bézier présentent un contrôle global signifie que le déplacement d'un point de contrôle modifie la forme de la courbe entière.
Une courbe de Bézier donnée peut être subdivisée en un point t = t0 en deux segments de Bézier qui se rejoignent au point correspondant à la valeur du paramètre t = t0.

Courbes B-Spline

La courbe de Bézier produite par la fonction de base de Bernstein a une flexibilité limitée.

Tout d'abord, le nombre de sommets de polygones spécifiés fixe l'ordre du polynôme résultant qui définit la courbe.
La deuxième caractéristique limite est que la valeur de la fonction de fusion est différente de zéro pour toutes les valeurs de paramètre sur toute la courbe.

La base B-spline contient la base de Bernstein comme cas particulier. La base B-spline est non globale.

Une courbe B-spline est définie comme une combinaison linéaire de points de contrôle Pi et une fonction de base B-spline $N_{i,}$ k (t) donné par

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$

Où,

{$p_{i}$: i = 0, 1, 2… .n} sont les points de contrôle
k est l'ordre des segments polynomiaux de la courbe B-spline. L'ordre k signifie que la courbe est composée de segments polynomiaux par morceaux de degré k - 1,
la $N_{i,k}(t)$sont les «fonctions de fusion B-spline normalisées». Ils sont décrits par l'ordre k et par une suite non décroissante de nombres réels appelée normalement «séquence de nœuds».

$${t_{i}:i = 0, ... n + K}$$

Les fonctions N _i , k sont décrites comme suit -

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$

et si k> 1,

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

Propriétés de la courbe B-spline

Les courbes B-spline ont les propriétés suivantes -

La somme des fonctions de base B-spline pour toute valeur de paramètre est 1.
Chaque fonction de base est positive ou nulle pour toutes les valeurs de paramètre.
Chaque fonction de base a précisément une valeur maximale, sauf pour k = 1.
L'ordre maximum de la courbe est égal au nombre de sommets du polygone de définition.
Le degré du polynôme B-spline est indépendant du nombre de sommets du polygone de définition.
La B-spline permet le contrôle local de la surface de la courbe car chaque sommet affecte la forme d'une courbe uniquement sur une plage de valeurs de paramètres où sa fonction de base associée est différente de zéro.
La courbe présente la propriété de diminution de la variation.
La courbe suit généralement la forme du polygone de définition.
Toute transformation affine peut être appliquée à la courbe en l'appliquant aux sommets du polygone de définition.
La ligne courbe dans la coque convexe de son polygone de définition.

Surfaces polygonales

Les objets sont représentés comme une collection de surfaces. La représentation d'objets 3D est divisée en deux catégories.

Boundary Representations (B-reps) - Il décrit un objet 3D comme un ensemble de surfaces qui sépare l'intérieur de l'objet de l'environnement.
Space–partitioning representations - Il est utilisé pour décrire les propriétés intérieures, en partitionnant la région spatiale contenant un objet en un ensemble de petits solides contigus non superposés (généralement des cubes).

La représentation de limite la plus couramment utilisée pour un objet graphique 3D est un ensemble de polygones de surface qui entourent l'intérieur de l'objet. De nombreux systèmes graphiques utilisent cette méthode. Un ensemble de polygones est stocké pour la description de l'objet. Cela simplifie et accélère le rendu de surface et l'affichage de l'objet puisque toutes les surfaces peuvent être décrites avec des équations linéaires.

Les surfaces polygonales sont courantes dans les applications de conception et de modélisation de solides, car leur wireframe displaypeut être fait rapidement pour donner une indication générale de la structure de la surface. Ensuite, des scènes réalistes sont produites en interpolant des motifs d'ombrage sur la surface du polygone pour éclairer.

Tables de polygones

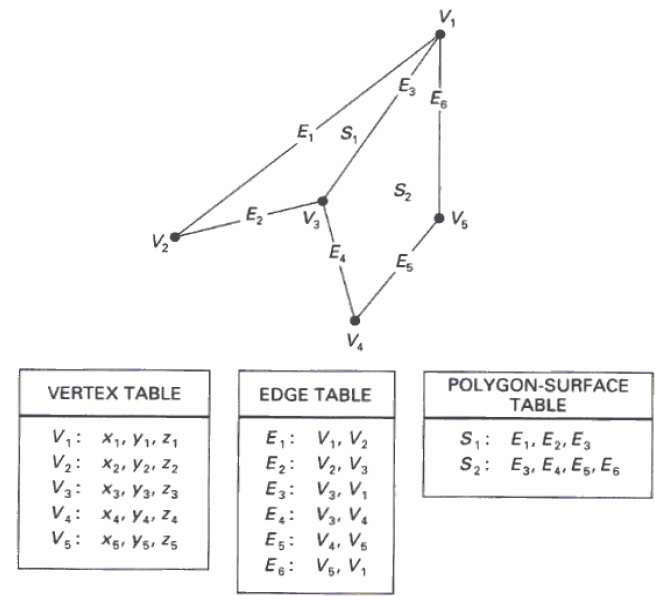
Dans cette méthode, la surface est spécifiée par l'ensemble des coordonnées de sommet et des attributs associés. Comme le montre la figure suivante, il y a cinq sommets, de v ₁ à v ₅ .

Chaque sommet stocke les informations de coordonnées x, y et z qui sont représentées dans le tableau par v ₁ : x ₁ , y ₁ , z ₁ .
La table Edge est utilisée pour stocker les informations de bord du polygone. Dans la figure suivante, l'arête E ₁ se situe entre les sommets v ₁ et v ₂ qui est représenté dans le tableau par E ₁ : v ₁ , v ₂ .
La table de surface de polygone stocke le nombre de surfaces présentes dans le polygone. D'après la figure suivante, la surface S ₁ est couverte par les arêtes E ₁ , E ₂ et E ₃ qui peuvent être représentées dans le tableau des surfaces polygonales par S ₁ : E ₁ , E ₂ et E ₃ .

Equations de plan

L'équation pour la surface plane peut être exprimée comme -

Axe + Par + Cz + D = 0

Où (x, y, z) est un point quelconque sur le plan, et les coefficients A, B, C et D sont des constantes décrivant les propriétés spatiales du plan. Nous pouvons obtenir les valeurs de A, B, C et D en résolvant un ensemble de trois équations planes en utilisant les valeurs de coordonnées pour trois points non colinéaires dans le plan. Supposons que trois sommets du plan soient (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) et (x ₃ , y ₃ , z ₃ ).

Résolvons les équations simultanées suivantes pour les rapports A / D, B / D et C / D. Vous obtenez les valeurs de A, B, C et D.

(A / D) x ₁ + (B / D) y ₁ + (C / D) z ₁ = -1

(A / D) x ₂ + (B / D) y ₂ + (C / D) z ₂ = -1

(A / D) x ₃ + (B / D) y ₃ + (C / D) z ₃ = -1

Pour obtenir les équations ci-dessus sous forme déterminante, appliquez la règle de Cramer aux équations ci-dessus.

$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

Pour tout point (x, y, z) avec les paramètres A, B, C et D, on peut dire que -

Ax + By + Cz + D ≠ 0 signifie que le point n'est pas sur le plan.
Ax + By + Cz + D <0 signifie que le point est à l'intérieur de la surface.
Ax + By + Cz + D> 0 signifie que le point est à l'extérieur de la surface.

Maillages polygonaux

Les surfaces et les solides 3D peuvent être approximés par un ensemble d'éléments polygonaux et linéaires. Ces surfaces sont appeléespolygonal meshes. Dans le maillage polygonal, chaque arête est partagée par au plus deux polygones. L'ensemble des polygones ou des faces forment ensemble la «peau» de l'objet.

Cette méthode peut être utilisée pour représenter une large classe de solides / surfaces dans les graphiques. Un maillage polygonal peut être rendu à l'aide d'algorithmes de suppression de surface cachée. Le maillage polygonal peut être représenté de trois façons -

Représentation explicite
Pointeurs vers une liste de sommets
Pointeurs vers une liste d'arêtes

Avantages

Il peut être utilisé pour modéliser presque n'importe quel objet.
Ils sont faciles à représenter comme une collection de sommets.
Ils sont faciles à transformer.
Ils sont faciles à dessiner sur écran d'ordinateur.

Désavantages

Les surfaces courbes ne peuvent être décrites qu'approximativement.
Il est difficile de simuler certains types d'objets comme des cheveux ou un liquide.

Lorsque nous visualisons une image contenant des objets et des surfaces non transparents, nous ne pouvons pas voir les objets de la vue qui sont derrière des objets plus proches des yeux. Nous devons supprimer ces surfaces cachées pour obtenir une image d'écran réaliste. L'identification et la suppression de ces surfaces s'appelleHidden-surface problem.

Il existe deux approches pour supprimer les problèmes de surface cachés - Object-Space method et Image-space method. La méthode de l'espace objet est implémentée dans le système de coordonnées physiques et la méthode de l'espace image est implémentée dans le système de coordonnées de l'écran.

Lorsque nous voulons afficher un objet 3D sur un écran 2D, nous devons identifier les parties d'un écran qui sont visibles à partir d'une position de visualisation choisie.

Méthode du tampon de profondeur (Z-Buffer)

Cette méthode est développée par Cutmull. C'est une approche de l'espace image. L'idée de base est de tester la profondeur Z de chaque surface pour déterminer la surface (visible) la plus proche.

Dans cette méthode, chaque surface est traitée séparément une position de pixel à la fois sur la surface. Les valeurs de profondeur d'un pixel sont comparées et la surface la plus proche (z la plus petite) détermine la couleur à afficher dans le tampon de trame.

Il est appliqué très efficacement sur les surfaces de polygone. Les surfaces peuvent être traitées dans n'importe quel ordre. Pour remplacer les polygones les plus proches des polygones éloignés, deux tampons nommésframe buffer et depth buffer, sont utilisés.

Depth buffer est utilisé pour stocker les valeurs de profondeur pour la position (x, y), au fur et à mesure que les surfaces sont traitées (0 ≤ profondeur ≤ 1).

le frame buffer est utilisé pour stocker la valeur d'intensité de la valeur de couleur à chaque position (x, y).

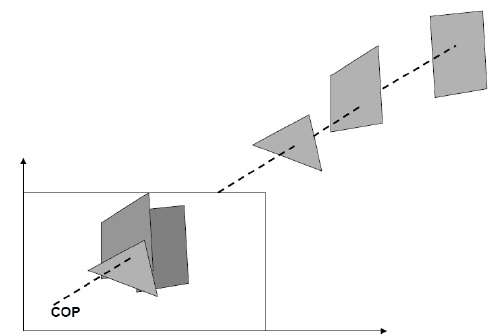
Les coordonnées z sont généralement normalisées à la plage [0, 1]. La valeur 0 pour la coordonnée z indique le volet de détourage arrière et 1 valeur pour les coordonnées z indique le volet de détourage avant.

Algorithme

Step-1 - Réglez les valeurs du tampon -

Tampon de profondeur (x, y) = 0

Framebuffer (x, y) = couleur d'arrière-plan

Step-2 - Traitez chaque polygone (un à la fois)

Pour chaque position de pixel projetée (x, y) d'un polygone, calculez la profondeur z.

Si Z> tampon de profondeur (x, y)

Calculer la couleur de la surface,

définir le tampon de profondeur (x, y) = z,

framebuffer (x, y) = couleur de surface (x, y)

Avantages

Il est facile à mettre en œuvre.
Il réduit le problème de vitesse s'il est implémenté dans le matériel.
Il traite un objet à la fois.

Désavantages

Cela nécessite une grande mémoire.
C'est un processus qui prend du temps.

Méthode de scan-line

C'est une méthode d'espace image pour identifier la surface visible. Cette méthode a une information de profondeur pour une seule ligne de balayage. Afin d'exiger une ligne de balayage des valeurs de profondeur, nous devons regrouper et traiter tous les polygones coupant une ligne de balayage donnée en même temps avant de traiter la prochaine ligne de balayage. Deux tableaux importants,edge table et polygon table, sont maintenus pour cela.

The Edge Table - Il contient les coordonnées des extrémités de chaque ligne de la scène, la pente inverse de chaque ligne et des pointeurs dans la table des polygones pour connecter les arêtes aux surfaces.

The Polygon Table - Il contient les coefficients du plan, les propriétés du matériau de surface, d'autres données de surface et peut être des pointeurs vers la table d'arêtes.

Pour faciliter la recherche de surfaces traversant une ligne de balayage donnée, une liste active d'arêtes est formée. La liste active ne stocke que les arêtes qui traversent la ligne de balayage dans l'ordre croissant de x. Un drapeau est également établi pour chaque surface pour indiquer si une position le long d'une ligne de balayage est à l'intérieur ou à l'extérieur de la surface.

Les positions des pixels sur chaque ligne de balayage sont traitées de gauche à droite. À l'intersection gauche avec une surface, le drapeau de surface est activé et à droite, le drapeau est désactivé. Vous ne devez effectuer des calculs de profondeur que lorsque plusieurs surfaces ont leurs indicateurs activés à une certaine position de la ligne de balayage.

Méthode de subdivision de la zone

La méthode de subdivision de zone tire parti de la localisation des zones de vue qui représentent une partie d'une seule surface. Divisez la zone de visualisation totale en rectangles de plus en plus petits jusqu'à ce que chaque petite zone soit la projection d'une partie d'une seule surface visible ou aucune surface du tout.

Continuez ce processus jusqu'à ce que les subdivisions soient facilement analysées comme appartenant à une seule surface ou jusqu'à ce qu'elles soient réduites à la taille d'un seul pixel. Une manière simple de le faire est de diviser successivement la zone en quatre parties égales à chaque étape. Il existe quatre relations possibles qu'une surface peut avoir avec une limite de zone spécifiée.

Surrounding surface - Celui qui entoure complètement la zone.
Overlapping surface - Un qui est en partie à l'intérieur et en partie à l'extérieur de la zone.
Inside surface - Un qui est complètement à l'intérieur de la zone.
Outside surface - Un qui est complètement en dehors de la zone.

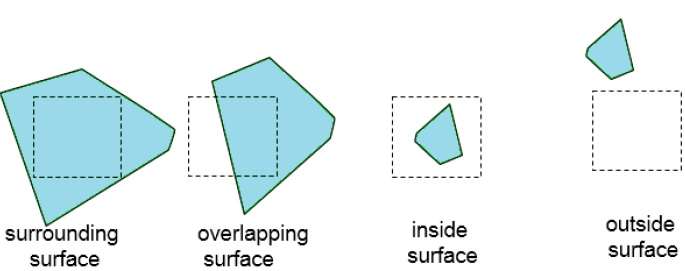
Les tests pour déterminer la visibilité de la surface dans une zone peuvent être énoncés en fonction de ces quatre classifications. Aucune autre subdivision d'une zone spécifiée n'est nécessaire si l'une des conditions suivantes est vraie -

Toutes les surfaces sont des surfaces extérieures par rapport à la zone.
Une seule surface intérieure, superposée ou environnante se trouve dans la zone.
Une surface environnante masque toutes les autres surfaces dans les limites de la zone.

Détection de la face arrière

Une méthode rapide et simple de l'espace objet pour identifier les faces arrière d'un polyèdre est basée sur les tests "intérieur-extérieur". Un point (x, y, z) est "à l'intérieur" d'une surface de polygone avec les paramètres de plan A, B, C et D si Lorsqu'un point intérieur est le long de la ligne de visée vers la surface, le polygone doit être une face arrière ( nous sommes à l'intérieur de ce visage et ne pouvons pas voir l'avant de celui-ci depuis notre position de vision).

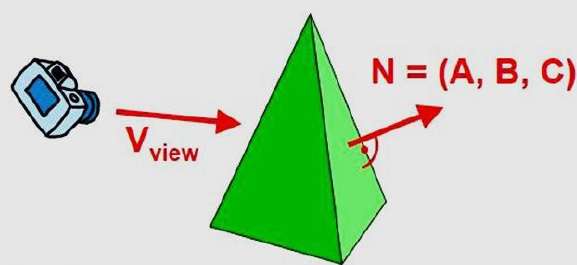
On peut simplifier ce test en considérant le vecteur normal N à une surface de polygone, qui a des composantes cartésiennes (A, B, C).

En général, si V est un vecteur dans la direction de visualisation à partir de la position de l'œil (ou de la «caméra»), alors ce polygone est une face arrière si

V.N > 0

De plus, si les descriptions d'objets sont converties en coordonnées de projection et que votre direction de visualisation est parallèle à l'axe z de visualisation, alors -

V = (0, 0, V _z ) et V.N = V _Z C

De sorte qu'il suffit de considérer le signe de C comme la composante du vecteur normal N.

Dans un système de visualisation droitier avec direction de visualisation le long du négatif $Z_{V}$axe, le polygone est une face arrière si C <0. De plus, nous ne pouvons voir aucune face dont la normale a la composante z C = 0, puisque votre direction de visualisation est vers ce polygone. Ainsi, en général, nous pouvons étiqueter n'importe quel polygone comme face arrière si son vecteur normal a une valeur de composante az -

C <= 0

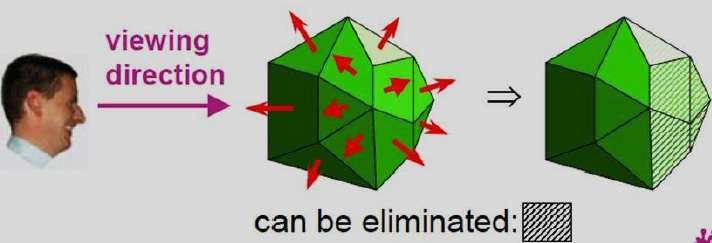
Des méthodes similaires peuvent être utilisées dans les emballages qui utilisent un système de visualisation pour gaucher. Dans ces packages, les paramètres de plan A, B, C et D peuvent être calculés à partir des coordonnées des sommets du polygone spécifiées dans le sens des aiguilles d'une montre (contrairement au sens anti-horaire utilisé dans un système droitier).

En outre, les faces arrière ont des vecteurs normaux qui pointent loin de la position de visualisation et sont identifiées par C> = 0 lorsque la direction de visualisation est le long du positif $Z_{v}$axe. En examinant le paramètre C pour les différents plans définissant un objet, nous pouvons identifier immédiatement toutes les faces arrière.

Méthode A-Buffer

La méthode A-buffer est une extension de la méthode Depth-buffer. La méthode A-buffer est une méthode de détection de visibilité développée aux Lucas Film Studios pour le système de rendu Renders Everything You Ever Saw (REYES).

Le tampon A développe la méthode du tampon de profondeur pour autoriser les transparents. La structure de données clé dans le tampon A est le tampon d'accumulation.

Chaque position dans le tampon A a deux champs -

Depth field - Il stocke un nombre réel positif ou négatif
Intensity field - Il stocke des informations d'intensité de surface ou une valeur de pointeur

Si profondeur> = 0, le nombre stocké à cette position est la profondeur d'une seule surface chevauchant la zone de pixels correspondante. Le champ d'intensité stocke ensuite les composants RVB de la couleur de surface à ce point et le pourcentage de couverture de pixels.

Si la profondeur <0, cela indique les contributions de plusieurs surfaces à l'intensité des pixels. Le champ d'intensité stocke ensuite un pointeur vers une liste liée de données de surface. Le tampon de surface dans le tampon A comprend -

Composants d'intensité RVB
Paramètre d'opacité
Depth
Pourcentage de couverture de zone
Identificateur de surface

L'algorithme se déroule comme l'algorithme du tampon de profondeur. Les valeurs de profondeur et d'opacité sont utilisées pour déterminer la couleur finale d'un pixel.

Méthode de tri en profondeur

La méthode de tri en profondeur utilise à la fois l'espace image et les opérations d'espace objet. La méthode de tri en profondeur remplit deux fonctions de base -

Tout d'abord, les surfaces sont triées par ordre de profondeur décroissante.
Deuxièmement, les surfaces sont converties par balayage dans l'ordre, en commençant par la surface de plus grande profondeur.

La conversion par balayage des surfaces polygonales est effectuée dans l'espace image. Cette méthode de résolution du problème de la surface cachée est souvent appeléepainter's algorithm. La figure suivante montre l'effet du tri en profondeur -

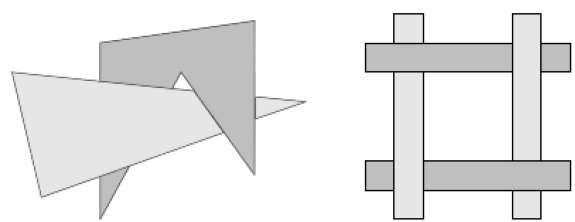
L'algorithme commence par trier par profondeur. Par exemple, l'estimation initiale de «profondeur» d'un polygone peut être considérée comme la valeur z la plus proche de n'importe quel sommet du polygone.

Prenons le polygone P à la fin de la liste. Considérons tous les polygones Q dont les étendues z chevauchent les P. Avant de dessiner P, nous faisons les tests suivants. Si l'un des tests suivants est positif, nous pouvons supposer que P peut être tiré avant Q.

Les x-extents ne se chevauchent-ils pas?
Les étendues y ne se chevauchent-elles pas?
P est-il entièrement du côté opposé du plan de Q du point de vue?
Q est-il entièrement du même côté du plan de P que le point de vue?
Les projections des polygones ne se chevauchent-elles pas?

Si tous les tests échouent, alors nous divisons P ou Q en utilisant le plan de l'autre. Les nouveaux polygones coupés s'insèrent dans l'ordre de profondeur et le processus se poursuit. Théoriquement, ce partitionnement pourrait générer O (n ² ) polygones individuels, mais en pratique, le nombre de polygones est beaucoup plus petit.

Arbres de partition d'espace binaire (BSP)

Le partitionnement de l'espace binaire est utilisé pour calculer la visibilité. Pour construire les arbres BSP, il faut commencer par des polygones et étiqueter toutes les arêtes. Si vous ne traitez qu'un seul bord à la fois, étendez chaque bord afin qu'il divise le plan en deux. Placez le premier bord de l'arbre en tant que racine. Ajoutez les arêtes suivantes selon qu'elles sont à l'intérieur ou à l'extérieur. Les arêtes qui couvrent l'extension d'une arête qui se trouve déjà dans l'arborescence sont divisées en deux et les deux sont ajoutées à l'arborescence.

À partir de la figure ci-dessus, prenez d'abord A en tant que racine.
Faites une liste de tous les nœuds de la figure (a).
Mettez tous les nœuds devant root A sur le côté gauche du nœud A et placez tous ces nœuds derrière la racine A sur le côté droit comme indiqué sur la figure (b).
Traitez d'abord tous les nœuds avant, puis les nœuds à l'arrière.
Comme le montre la figure (c), nous allons d'abord traiter le nœud B. Comme il n'y a rien devant le nœudB, nous avons mis NIL. Cependant, nous avons nodeC à l'arrière du nœud B, donc noeud C ira sur le côté droit du nœud B.
Répétez le même processus pour le nœud D.

Un mathématicien franco-américain, le Dr Benoit Mandelbrot, a découvert Fractals. Le mot fractale est dérivé d'un mot latin fractus qui signifie cassé.

Que sont les fractales?

Les fractales sont des images très complexes générées par un ordinateur à partir d'une seule formule. Ils sont créés à l'aide d'itérations. Cela signifie qu'une formule est répétée avec des valeurs légèrement différentes encore et encore, en tenant compte des résultats de l'itération précédente.

Les fractales sont utilisées dans de nombreux domaines tels que -

Astronomy - Pour analyser les galaxies, les anneaux de Saturne, etc.
Biology/Chemistry - Pour représenter des cultures de bactéries, des réactions chimiques, l'anatomie humaine, des molécules, des plantes,
Others - Pour représenter les nuages, le littoral et les frontières, la compression de données, la diffusion, l'économie, l'art fractal, la musique fractale, les paysages, les effets spéciaux, etc.

Génération de fractales

Les fractales peuvent être générées en répétant la même forme encore et encore, comme illustré dans la figure suivante. La figure (a) montre un triangle équilatéral. Dans la figure (b), nous pouvons voir que le triangle est répété pour créer une forme en étoile. Dans la figure (c), nous pouvons voir que la forme d'étoile de la figure (b) est répétée encore et encore pour créer une nouvelle forme.

Nous pouvons faire un nombre illimité d'itérations pour créer une forme souhaitée. En termes de programmation, la récursivité est utilisée pour créer de telles formes.

Fractales géométriques

Les fractales géométriques traitent des formes trouvées dans la nature qui ont des dimensions non entières ou fractales. Pour construire géométriquement une fractale auto-similaire déterministe (non aléatoire), nous commençons par une forme géométrique donnée, appelée leinitiator. Les sous-parties de l'initiateur sont ensuite remplacées par un modèle, appelé legenerator.

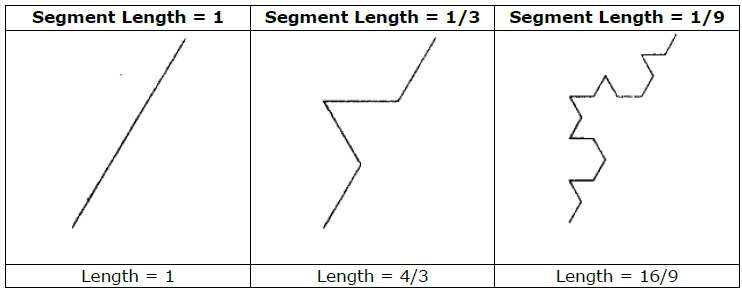
A titre d'exemple, si nous utilisons l'initiateur et le générateur illustrés dans la figure ci-dessus, nous pouvons construire un bon modèle en le répétant. Chaque segment de ligne droite dans l'initiateur est remplacé par quatre segments de ligne de même longueur à chaque étape. Le facteur d'échelle est 1/3, donc la dimension fractale est D = ln 4 / ln 3 ≈ 1,2619.

De plus, la longueur de chaque segment de ligne dans l'initiateur augmente d'un facteur 4/3 à chaque étape, de sorte que la longueur de la courbe fractale tend vers l'infini à mesure que plus de détails sont ajoutés à la courbe, comme indiqué dans la figure suivante -

L'animation, c'est donner vie à n'importe quel objet en infographie. Il a le pouvoir d'injecter de l'énergie et des émotions dans les objets les plus apparemment inanimés. L'animation assistée par ordinateur et l'animation générée par ordinateur sont deux catégories d'animation par ordinateur. Il peut être présenté via un film ou une vidéo.

L'idée de base derrière l'animation est de lire les images enregistrées à des taux suffisamment rapides pour tromper l'œil humain en les interprétant comme un mouvement continu. L'animation peut donner vie à une série d'images mortes. L'animation peut être utilisée dans de nombreux domaines tels que le divertissement, la conception assistée par ordinateur, la visualisation scientifique, la formation, l'éducation, le commerce électronique et l'art informatique.

Techniques d'animation

Les animateurs ont inventé et utilisé une variété de techniques d'animation différentes. Fondamentalement, il existe six techniques d'animation dont nous discuterons une par une dans cette section.

Animation traditionnelle (image par image)

Traditionnellement, la plupart des animations étaient réalisées à la main. Toutes les images d'une animation devaient être dessinées à la main. Étant donné que chaque seconde d'animation nécessite 24 images (film), la quantité d'efforts requis pour créer même le plus court des films peut être énorme.

Images clés

Dans cette technique, un storyboard est mis en page, puis les artistes dessinent les principales images de l'animation. Les cadres majeurs sont ceux dans lesquels des changements importants ont lieu. Ce sont les points clés de l'animation. Les images clés nécessitent que l'animateur spécifie des positions critiques ou clés pour les objets. L'ordinateur remplit alors automatiquement les images manquantes en interpolant en douceur entre ces positions.

De procédure

Dans une animation procédurale, les objets sont animés par une procédure - un ensemble de règles - et non par des images clés. L'animateur spécifie les règles et les conditions initiales et exécute la simulation. Les règles sont souvent basées sur des règles physiques du monde réel exprimées par des équations mathématiques.

Comportementale

Dans l'animation comportementale, un personnage autonome détermine ses propres actions, au moins dans une certaine mesure. Cela donne au personnage une certaine capacité à improviser et libère l'animateur de la nécessité de spécifier chaque détail du mouvement de chaque personnage.

Basé sur les performances (Motion Capture)

Une autre technique est la capture de mouvement, dans laquelle des capteurs magnétiques ou basés sur la vision enregistrent les actions d'un objet humain ou animal en trois dimensions. Un ordinateur utilise ensuite ces données pour animer l'objet.

Cette technologie a permis à un certain nombre d'athlètes célèbres de fournir les actions des personnages dans les jeux vidéo sportifs. La capture de mouvement est très populaire auprès des animateurs, principalement parce que certaines des actions humaines courantes peuvent être capturées avec une relative facilité. Cependant, il peut y avoir de sérieux écarts entre les formes ou les dimensions du sujet et le caractère graphique et cela peut conduire à des problèmes d'exécution exacte.

Basé sur la physique (dynamique)

Contrairement au cadrage clé et au cinéma, la simulation utilise les lois de la physique pour générer des mouvements d'images et d'autres objets. Les simulations peuvent être facilement utilisées pour produire des séquences légèrement différentes tout en conservant un réalisme physique. Deuxièmement, les simulations en temps réel permettent un plus haut degré d'interactivité où la personne réelle peut manœuvrer les actions du personnage simulé.

En revanche, les applications basées sur les images clés et les mouvements de sélection et de modification des mouvements forment une bibliothèque pré-calculée de mouvements. Un inconvénient dont souffre la simulation est l'expertise et le temps nécessaires pour fabriquer à la main les systèmes de commande appropriés.

Encadrement clé

Une image clé est une image dans laquelle nous définissons les changements d'animation. Chaque image est une image clé lorsque nous créons une animation image par image. Quand quelqu'un crée une animation 3D sur un ordinateur, il ne spécifie généralement pas la position exacte d'un objet donné sur chaque image. Ils créent des images clés.

Les images clés sont des images importantes au cours desquelles un objet change de taille, de direction, de forme ou d’autres propriétés. L'ordinateur détermine alors toutes les images intermédiaires et fait gagner un temps extrême à l'animateur. Les illustrations suivantes représentent les cadres dessinés par l'utilisateur et les cadres générés par ordinateur.

Morphing

La transformation des formes d'objets d'une forme à une autre est appelée morphing. C'est l'une des transformations les plus compliquées.

Une morphologie donne l'impression que deux images se fondent l'une dans l'autre avec un mouvement très fluide. En termes techniques, deux images sont déformées et un fondu se produit entre elles.