Affichage et découpage
La principale utilisation du détourage en infographie consiste à supprimer des objets, des lignes ou des segments de ligne qui se trouvent en dehors du volet d'affichage. La transformation de visualisation est insensible à la position des points par rapport au volume de visualisation - en particulier les points situés derrière le spectateur - et il est nécessaire de supprimer ces points avant de générer la vue.
Coupure de point
Découper un point d'une fenêtre donnée est très simple. Considérez la figure suivante, où le rectangle indique la fenêtre. L'écrêtage de point nous indique si le point donné (X, Y) se trouve ou non dans la fenêtre donnée; et décide si nous utiliserons les coordonnées minimum et maximum de la fenêtre.
La coordonnée X du point donné est à l'intérieur de la fenêtre, si X se situe entre Wx1 ≤ X ≤ Wx2. De la même manière, la coordonnée Y du point donné est à l'intérieur de la fenêtre, si Y se situe entre Wy1 ≤ Y ≤ Wy2.

Coupure de ligne
Le concept de découpage de ligne est le même que celui de découpage de points. Dans le détourage de ligne, nous allons couper la partie de la ligne qui est à l'extérieur de la fenêtre et ne conserver que la partie qui se trouve à l'intérieur de la fenêtre.
Coupures de la ligne Cohen-Sutherland
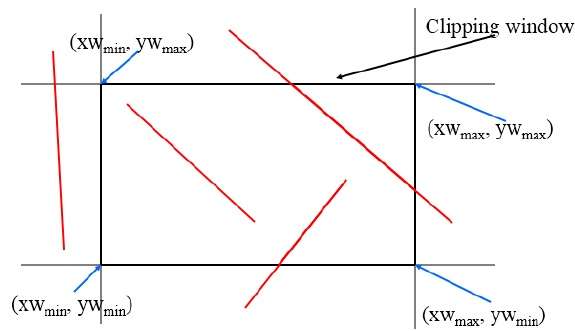
Cet algorithme utilise la fenêtre de découpage comme illustré dans la figure suivante. La coordonnée minimale de la région de découpage est $ (XW_ {min,} YW_ {min}) $ et la coordonnée maximale de la région de découpage est $ (XW_ {max,} YW_ {max}) $.
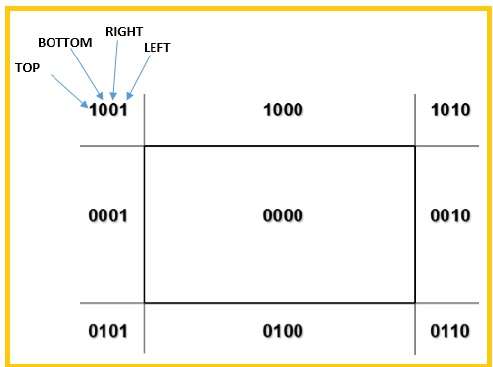
Nous utiliserons 4 bits pour diviser toute la région. Ces 4 bits représentent le haut, le bas, la droite et la gauche de la région, comme illustré dans la figure suivante. Ici leTOP et LEFT bit est mis à 1 car c'est le TOP-LEFT coin.
Il y a 3 possibilités pour la ligne -
La ligne peut être complètement à l'intérieur de la fenêtre (Cette ligne doit être acceptée).
La ligne peut être complètement en dehors de la fenêtre (Cette ligne sera complètement supprimée de la région).
La ligne peut être partiellement à l'intérieur de la fenêtre (nous trouverons le point d'intersection et ne dessinons que la partie de la ligne qui se trouve à l'intérieur de la région).
Algorithme
Step 1 - Attribuez un code de région pour chaque point de terminaison.
Step 2 - Si les deux terminaux ont un code de région 0000 puis acceptez cette ligne.
Step 3 - Sinon, effectuez la logique ANDopération pour les deux codes de région.
Step 3.1 - Si le résultat n'est pas 0000, puis rejetez la ligne.
Step 3.2 - Sinon, vous avez besoin d'écrêtage.
Step 3.2.1 - Choisissez une extrémité de la ligne qui se trouve à l'extérieur de la fenêtre.
Step 3.2.2 - Trouvez le point d'intersection à la limite de la fenêtre (basé sur le code de région).
Step 3.2.3 - Remplacez le point final par le point d'intersection et mettez à jour le code de région.
Step 3.2.4 - Répétez l'étape 2 jusqu'à ce que nous trouvions une ligne tronquée soit trivialement acceptée soit trivialement rejetée.
Step 4 - Répétez l'étape 1 pour les autres lignes.
Algorithme d'écrêtage de ligne Cyrus-Beck
Cet algorithme est plus efficace que l'algorithme de Cohen-Sutherland. Il utilise une représentation de ligne paramétrique et des produits scalaires simples.
L'équation paramétrique de la ligne est -
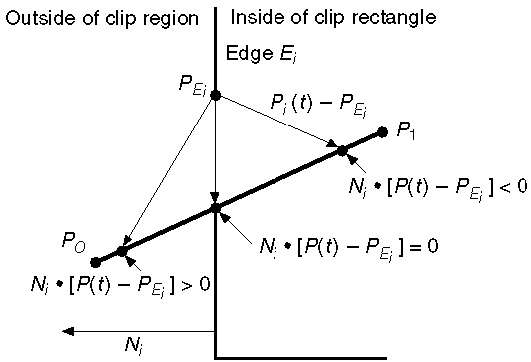
P0P1:P(t) = P0 + t(P1 - P0)Soit N i l'arête normale extérieure E i . Sélectionnez maintenant n'importe quel point arbitraire P Ei sur le bord E i puis le produit scalaire N i . [P (t) - P Ei ] détermine si le point P (t) est «à l'intérieur du bord du clip» ou «à l'extérieur» du bord du clip ou «Sur» le bord du clip.
Le point P (t) est à l'intérieur si N i . [P (t) - P Ei ] <0
Le point P (t) est extérieur si N i . [P (t) - P Ei ]> 0
Le point P (t) est sur l'arête si N i . [P (t) - P Ei ] = 0 (point d'intersection)
N i . [P (t) - P Ei ] = 0
N i . [P 0 + t (P 1 - P 0 ) - P Ei ] = 0 (Remplacement de P (t) par P 0 + t (P 1 - P 0 ))
N i . [P 0 - P Ei ] + N i .t [P 1 - P 0 ] = 0
N i . [P 0 - P Ei ] + N i ∙ tD = 0 (en remplaçant D par [P 1 - P 0 ])
N i . [P 0 - P Ei ] = - N i ∙ tD
L'équation pour t devient,
$$ t = \ tfrac {N_ {i}. [P_ {o} - P_ {Ei}]} {{- N_ {i} .D}} $$
Il est valable pour les conditions suivantes -
- N i ≠ 0 (l'erreur ne peut pas se produire)
- D ≠ 0 (P 1 ≠ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1 non parallèle à E i )
Découpage de polygones (algorithme Sutherland Hodgman)
Un polygone peut également être découpé en spécifiant la fenêtre de découpage. L'algorithme de découpage de polygones de Sutherland Hodgeman est utilisé pour le découpage de polygones. Dans cet algorithme, tous les sommets du polygone sont découpés contre chaque bord de la fenêtre de découpage.
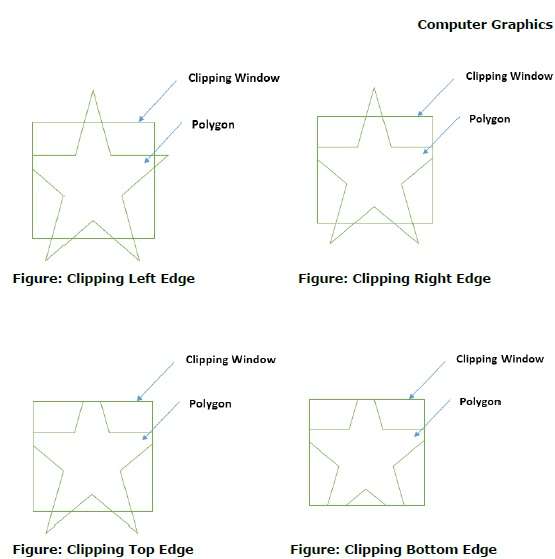
Tout d'abord, le polygone est découpé contre le bord gauche de la fenêtre de polygone pour obtenir de nouveaux sommets du polygone. Ces nouveaux sommets sont utilisés pour découper le polygone contre le bord droit, le bord supérieur, le bord inférieur de la fenêtre de découpage, comme illustré dans la figure suivante.
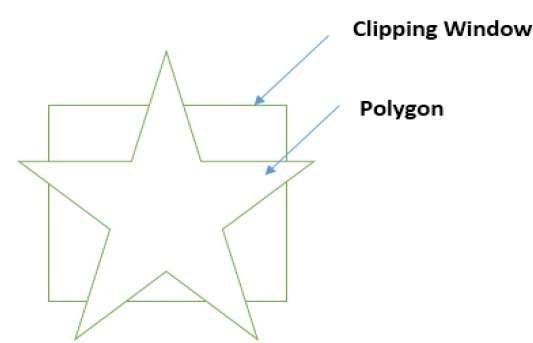
Lors du traitement d'une arête d'un polygone avec fenêtre de découpage, un point d'intersection est trouvé si l'arête n'est pas complètement à l'intérieur de la fenêtre de découpage et si une arête partielle du point d'intersection à l'arête extérieure est découpée. Les figures suivantes montrent des coupures de bord gauche, droit, supérieur et inférieur -
Coupure de texte
Diverses techniques sont utilisées pour fournir un découpage de texte dans une infographie. Cela dépend des méthodes utilisées pour générer des caractères et des exigences d'une application particulière. Il existe trois méthodes de découpage de texte qui sont répertoriées ci-dessous -
- Coupure de chaîne tout ou rien
- Coupure de tout ou aucun caractère
- Coupure de texte
La figure suivante montre tout ou aucun découpage de chaîne -
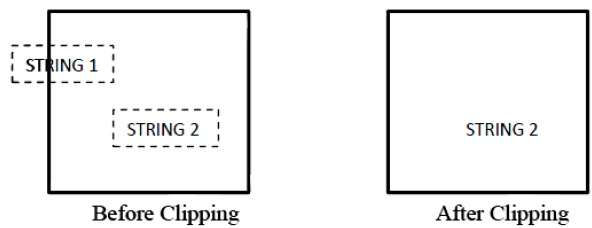
Dans la méthode de découpage de chaîne tout ou rien, soit nous conservons la chaîne entière, soit nous rejetons la chaîne entière en fonction de la fenêtre de découpage. Comme le montre la figure ci-dessus, STRING2 est entièrement à l'intérieur de la fenêtre de découpage donc nous la gardons et STRING1 n'étant que partiellement à l'intérieur de la fenêtre, nous rejetons.
La figure suivante montre le découpage de tous ou aucun caractère -
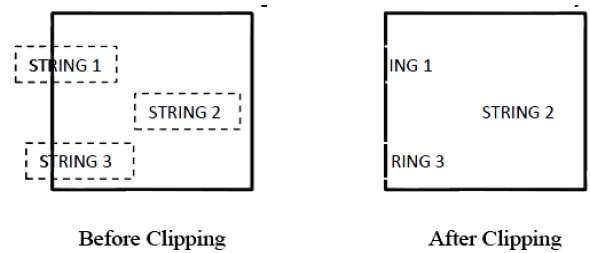
Cette méthode de découpage est basée sur des caractères plutôt que sur une chaîne entière. Dans cette méthode, si la chaîne est entièrement à l'intérieur de la fenêtre de découpage, nous la conservons. Si c'est partiellement à l'extérieur de la fenêtre, alors -
Vous rejetez uniquement la partie de la chaîne étant à l'extérieur
Si le caractère se trouve à la limite de la fenêtre de découpage, nous rejetons ce caractère entier et conservons la chaîne restante.
La figure suivante montre le découpage de texte -
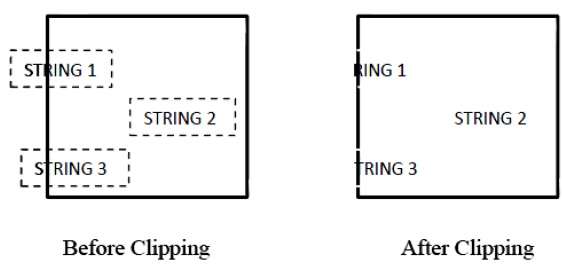
Cette méthode de découpage est basée sur des caractères plutôt que sur la chaîne entière. Dans cette méthode, si la chaîne est entièrement à l'intérieur de la fenêtre de découpage, nous la conservons. Si c'est partiellement à l'extérieur de la fenêtre, alors
Vous rejetez uniquement la partie de la chaîne à l'extérieur.
Si le caractère est à la limite de la fenêtre de découpage, nous ne supprimons que la partie du caractère qui se trouve en dehors de la fenêtre de découpage.
Graphiques Bitmap
Un bitmap est une collection de pixels qui décrit une image. C'est un type d'infographie que l'ordinateur utilise pour stocker et afficher des images. Dans ce type de graphiques, les images sont stockées petit à petit et sont donc appelées graphiques Bit-map. Pour une meilleure compréhension, considérons l'exemple suivant où nous dessinons un visage souriant à l'aide de graphiques bitmap.

Nous allons maintenant voir comment ce smiley est stocké petit à petit en infographie.
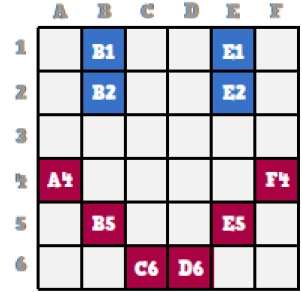
En observant de près le visage souriant d'origine, nous pouvons voir qu'il y a deux lignes bleues qui sont représentées par B1, B2 et E1, E2 dans la figure ci-dessus.
De la même manière, le smiley est représenté en utilisant les bits de combinaison de A4, B5, C6, D6, E5 et F4 respectivement.
Les principaux inconvénients des graphiques bitmap sont:
Nous ne pouvons pas redimensionner l'image bitmap. Si vous essayez de redimensionner, les pixels deviennent flous.
Les bitmaps colorés peuvent être très volumineux.