Détection de surface visible

Lorsque nous visualisons une image contenant des objets et des surfaces non transparents, nous ne pouvons pas voir les objets de la vue qui sont derrière des objets plus proches des yeux. Nous devons supprimer ces surfaces cachées pour obtenir une image d'écran réaliste. L'identification et la suppression de ces surfaces s'appelleHidden-surface problem.

Il existe deux approches pour supprimer les problèmes de surface cachés - Object-Space method et Image-space method. La méthode de l'espace objet est implémentée dans le système de coordonnées physiques et la méthode de l'espace image est implémentée dans le système de coordonnées de l'écran.

Lorsque nous voulons afficher un objet 3D sur un écran 2D, nous devons identifier les parties d'un écran qui sont visibles à partir d'une position de visualisation choisie.

Méthode du tampon de profondeur (Z-Buffer)

Cette méthode est développée par Cutmull. C'est une approche de l'espace image. L'idée de base est de tester la profondeur Z de chaque surface pour déterminer la surface (visible) la plus proche.

Dans cette méthode, chaque surface est traitée séparément une position de pixel à la fois sur la surface. Les valeurs de profondeur d'un pixel sont comparées et la surface la plus proche (z la plus petite) détermine la couleur à afficher dans le tampon de trame.

Il est appliqué très efficacement sur les surfaces de polygone. Les surfaces peuvent être traitées dans n'importe quel ordre. Pour remplacer les polygones les plus proches des polygones éloignés, deux tampons nommésframe buffer et depth buffer, sont utilisés.

Depth buffer est utilisé pour stocker les valeurs de profondeur pour la position (x, y), au fur et à mesure que les surfaces sont traitées (0 ≤ profondeur ≤ 1).

le frame buffer est utilisé pour stocker la valeur d'intensité de la valeur de couleur à chaque position (x, y).

Les coordonnées z sont généralement normalisées à la plage [0, 1]. La valeur 0 pour la coordonnée z indique le volet de détourage arrière et 1 valeur pour les coordonnées z indique le volet de détourage avant.

Algorithme

Step-1 - Réglez les valeurs du tampon -

Tampon de profondeur (x, y) = 0

Framebuffer (x, y) = couleur d'arrière-plan

Step-2 - Traitez chaque polygone (un à la fois)

Pour chaque position de pixel projetée (x, y) d'un polygone, calculez la profondeur z.

Si Z> tampon de profondeur (x, y)

Calculer la couleur de la surface,

définir le tampon de profondeur (x, y) = z,

framebuffer (x, y) = couleur de surface (x, y)

Avantages

Il est facile à mettre en œuvre.
Il réduit le problème de vitesse s'il est implémenté dans le matériel.
Il traite un objet à la fois.

Désavantages

Cela nécessite une grande mémoire.
C'est un processus qui prend du temps.

Méthode Scan-Line

C'est une méthode d'espace image pour identifier la surface visible. Cette méthode a une information de profondeur pour une seule ligne de balayage. Afin d'exiger une ligne de balayage des valeurs de profondeur, nous devons regrouper et traiter tous les polygones coupant une ligne de balayage donnée en même temps avant de traiter la prochaine ligne de balayage. Deux tableaux importants,edge table et polygon table, sont maintenus pour cela.

The Edge Table - Il contient les coordonnées des extrémités de chaque ligne de la scène, la pente inverse de chaque ligne et des pointeurs dans la table des polygones pour connecter les arêtes aux surfaces.

The Polygon Table - Il contient les coefficients du plan, les propriétés du matériau de surface, d'autres données de surface et peut être des pointeurs vers la table d'arêtes.

Pour faciliter la recherche de surfaces traversant une ligne de balayage donnée, une liste active d'arêtes est formée. La liste active ne stocke que les arêtes qui traversent la ligne de balayage dans l'ordre croissant de x. Un drapeau est également établi pour chaque surface pour indiquer si une position le long d'une ligne de balayage est à l'intérieur ou à l'extérieur de la surface.

Les positions des pixels sur chaque ligne de balayage sont traitées de gauche à droite. À l'intersection gauche avec une surface, le drapeau de surface est activé et à droite, le drapeau est désactivé. Vous ne devez effectuer des calculs de profondeur que lorsque plusieurs surfaces ont leurs indicateurs activés à une certaine position de la ligne de balayage.

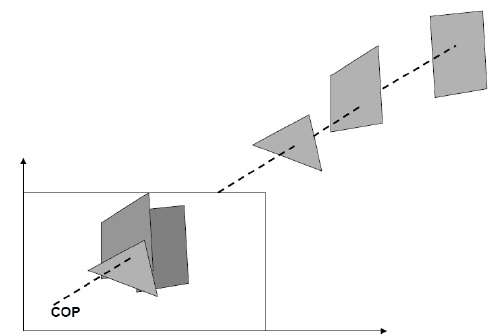
Méthode de subdivision de la zone

La méthode de subdivision de zone tire parti de la localisation des zones de vue qui représentent une partie d'une seule surface. Divisez la zone de visualisation totale en rectangles de plus en plus petits jusqu'à ce que chaque petite zone soit la projection d'une partie d'une seule surface visible ou aucune surface du tout.

Continuez ce processus jusqu'à ce que les subdivisions soient facilement analysées comme appartenant à une seule surface ou jusqu'à ce qu'elles soient réduites à la taille d'un seul pixel. Une manière simple de le faire est de diviser successivement la zone en quatre parties égales à chaque étape. Il existe quatre relations possibles qu'une surface peut avoir avec une limite de zone spécifiée.

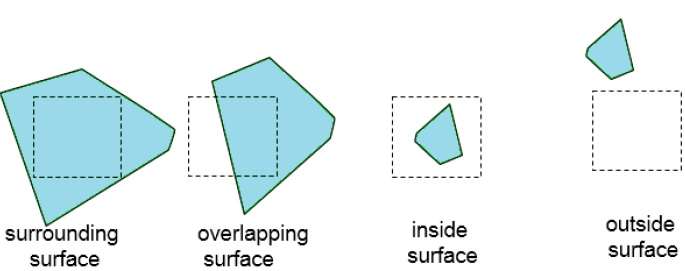
Surrounding surface - Celui qui entoure complètement la zone.
Overlapping surface - Un qui est en partie à l'intérieur et en partie à l'extérieur de la zone.
Inside surface - Un qui est complètement à l'intérieur de la zone.
Outside surface - Un qui est complètement en dehors de la zone.

Les tests pour déterminer la visibilité de la surface dans une zone peuvent être énoncés en fonction de ces quatre classifications. Aucune autre subdivision d'une zone spécifiée n'est nécessaire si l'une des conditions suivantes est vraie -

Toutes les surfaces sont des surfaces extérieures par rapport à la zone.
Une seule surface intérieure, superposée ou environnante se trouve dans la zone.
Une surface environnante masque toutes les autres surfaces dans les limites de la zone.

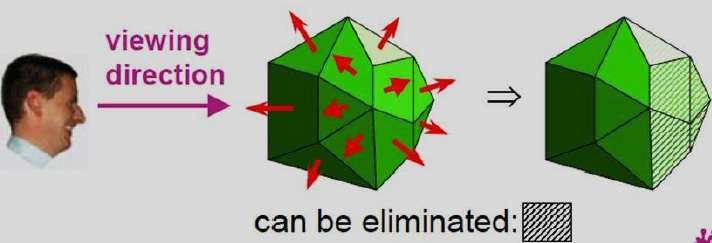
Détection de la face arrière

Une méthode rapide et simple de l'espace objet pour identifier les faces arrière d'un polyèdre est basée sur les tests "intérieur-extérieur". Un point (x, y, z) est "à l'intérieur" d'une surface de polygone avec les paramètres de plan A, B, C et D si Lorsqu'un point intérieur est le long de la ligne de visée vers la surface, le polygone doit être une face arrière ( nous sommes à l'intérieur de ce visage et ne pouvons pas voir l'avant de celui-ci depuis notre position de vision).

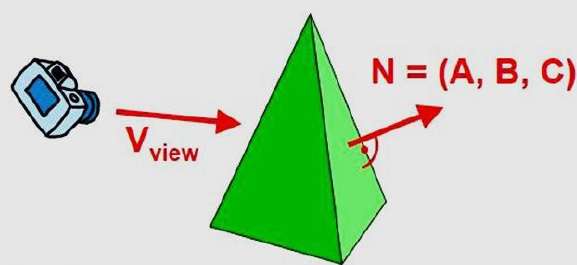
On peut simplifier ce test en considérant le vecteur normal N à une surface de polygone, qui a des composantes cartésiennes (A, B, C).

En général, si V est un vecteur dans la direction de visualisation à partir de la position de l'œil (ou de la «caméra»), alors ce polygone est une face arrière si

V.N > 0

De plus, si les descriptions d'objets sont converties en coordonnées de projection et que votre direction de visualisation est parallèle à l'axe z de visualisation, alors -

V = (0, 0, V _z ) et V.N = V _Z C

De sorte qu'il suffit de considérer le signe de C comme la composante du vecteur normal N.

Dans un système de visualisation droitier avec une direction de visualisation le long de l'axe négatif $ Z_ {V} $, le polygone est une face arrière si C <0. De plus, nous ne pouvons voir aucune face dont la normale a la composante z C = 0, puisque votre la direction d'observation est vers ce polygone. Ainsi, en général, nous pouvons étiqueter n'importe quel polygone comme face arrière si son vecteur normal a une valeur de composante az -

C <= 0

Des méthodes similaires peuvent être utilisées dans les emballages qui utilisent un système de visualisation pour gaucher. Dans ces packages, les paramètres de plan A, B, C et D peuvent être calculés à partir des coordonnées des sommets du polygone spécifiées dans le sens des aiguilles d'une montre (contrairement au sens anti-horaire utilisé dans un système droitier).

De plus, les faces arrière ont des vecteurs normaux qui pointent loin de la position de visualisation et sont identifiées par C> = 0 lorsque la direction de visualisation est le long de l'axe positif $ Z_ {v} $. En examinant le paramètre C pour les différents plans définissant un objet, nous pouvons identifier immédiatement toutes les faces arrière.

Méthode A-Buffer

La méthode A-buffer est une extension de la méthode Depth-buffer. La méthode A-buffer est une méthode de détection de visibilité développée aux Lucas Film Studios pour le système de rendu Renders Everything You Ever Saw (REYES).

Le tampon A développe la méthode du tampon de profondeur pour autoriser les transparents. La structure de données clé dans le tampon A est le tampon d'accumulation.

Chaque position dans le tampon A a deux champs -

Depth field - Il stocke un nombre réel positif ou négatif
Intensity field - Il stocke des informations d'intensité de surface ou une valeur de pointeur

Si profondeur> = 0, le nombre stocké à cette position est la profondeur d'une seule surface chevauchant la zone de pixels correspondante. Le champ d'intensité stocke ensuite les composants RVB de la couleur de surface à ce point et le pourcentage de couverture de pixels.

Si la profondeur <0, cela indique les contributions de plusieurs surfaces à l'intensité des pixels. Le champ d'intensité stocke ensuite un pointeur vers une liste liée de données de surface. Le tampon de surface dans le tampon A comprend -

Composants d'intensité RVB
Paramètre d'opacité
Depth
Pourcentage de couverture de zone
Identificateur de surface

L'algorithme se déroule comme l'algorithme du tampon de profondeur. Les valeurs de profondeur et d'opacité sont utilisées pour déterminer la couleur finale d'un pixel.

Méthode de tri en profondeur

La méthode de tri en profondeur utilise à la fois l'espace image et les opérations d'espace objet. La méthode de tri en profondeur remplit deux fonctions de base -

Tout d'abord, les surfaces sont triées par ordre de profondeur décroissante.
Deuxièmement, les surfaces sont converties par balayage dans l'ordre, en commençant par la surface de plus grande profondeur.

La conversion par balayage des surfaces polygonales est effectuée dans l'espace image. Cette méthode de résolution du problème de la surface cachée est souvent appeléepainter's algorithm. La figure suivante montre l'effet du tri en profondeur -

L'algorithme commence par trier par profondeur. Par exemple, l'estimation initiale de «profondeur» d'un polygone peut être considérée comme la valeur z la plus proche de n'importe quel sommet du polygone.

Prenons le polygone P à la fin de la liste. Considérons tous les polygones Q dont les étendues z chevauchent les P. Avant de dessiner P, nous faisons les tests suivants. Si l'un des tests suivants est positif, nous pouvons supposer que P peut être tiré avant Q.

Les x-extents ne se chevauchent-ils pas?
Les étendues y ne se chevauchent-elles pas?
P est-il entièrement du côté opposé du plan de Q du point de vue?
Q est-il entièrement du même côté du plan de P que le point de vue?
Les projections des polygones ne se chevauchent-elles pas?

Si tous les tests échouent, alors nous divisons P ou Q en utilisant le plan de l'autre. Les nouveaux polygones coupés s'insèrent dans l'ordre de profondeur et le processus se poursuit. Théoriquement, ce partitionnement pourrait générer O (n ² ) polygones individuels, mais en pratique, le nombre de polygones est beaucoup plus petit.

Arbres de partition d'espace binaire (BSP)

Le partitionnement de l'espace binaire est utilisé pour calculer la visibilité. Pour construire les arbres BSP, il faut commencer par des polygones et étiqueter toutes les arêtes. Si vous ne traitez qu'un seul bord à la fois, étendez chaque bord afin qu'il divise le plan en deux. Placez le premier bord de l'arbre en tant que racine. Ajoutez les arêtes suivantes selon qu'elles sont à l'intérieur ou à l'extérieur. Les arêtes qui couvrent l'extension d'une arête déjà présente dans l'arborescence sont divisées en deux et les deux sont ajoutées à l'arborescence.

À partir de la figure ci-dessus, prenez d'abord A en tant que racine.
Faites une liste de tous les nœuds de la figure (a).
Mettez tous les nœuds devant root A sur le côté gauche du nœud A et placez tous ces nœuds derrière la racine A sur le côté droit comme indiqué sur la figure (b).
Traitez d'abord tous les nœuds avant, puis les nœuds à l'arrière.
Comme le montre la figure (c), nous allons d'abord traiter le nœud B. Comme il n'y a rien devant le nœudB, nous avons mis NIL. Cependant, nous avons nodeC à l'arrière du nœud B, donc noeud C ira sur le côté droit du nœud B.
Répétez le même processus pour le nœud D.