Algorithme de génération de cercle

Dessiner un cercle sur l'écran est un peu complexe que de dessiner une ligne. Il existe deux algorithmes populaires pour générer un cercle -Bresenham’s Algorithm et Midpoint Circle Algorithm. Ces algorithmes sont basés sur l'idée de déterminer les points ultérieurs nécessaires pour dessiner le cercle. Laissez-nous discuter des algorithmes en détail -

L'équation du cercle est $ X ^ {2} + Y ^ {2} = r ^ {2}, $ où r est le rayon.

Algorithme de Bresenham

Nous ne pouvons pas afficher un arc continu sur l'affichage raster. Au lieu de cela, nous devons choisir la position de pixel la plus proche pour terminer l'arc.

Dans l'illustration suivante, vous pouvez voir que nous avons placé le pixel à l'emplacement (X, Y) et que nous devons maintenant décider où placer le pixel suivant - à N (X + 1, Y) ou à S (X + 1, Y-1).

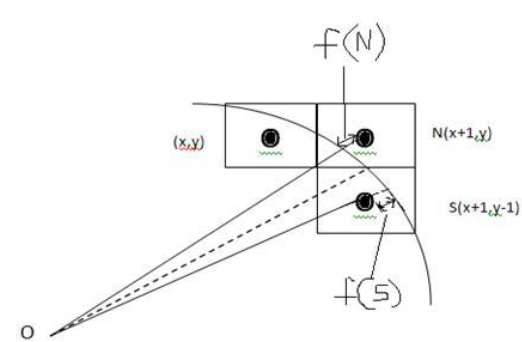
Cela peut être décidé par le paramètre de décision d.

• Si d <= 0, alors N (X + 1, Y) doit être choisi comme pixel suivant.
• Si d> 0, alors S (X + 1, Y-1) doit être choisi comme pixel suivant.

Algorithme

Step 1- Obtenez les coordonnées du centre du cercle et du rayon, et stockez-les respectivement en x, y et R. Réglez P = 0 et Q = R.

Step 2 - Régler le paramètre de décision D = 3 - 2R.

Step 3 - Répétez jusqu'à l'étape 8 pendant que P ≤ Q.

Step 4 - Appelez Draw Circle (X, Y, P, Q).

Step 5 - Augmentez la valeur de P.

Step 6 - Si D <0 alors D = D + 4P + 6.

Step 7 - Sinon, réglez R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Appelez Draw Circle (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

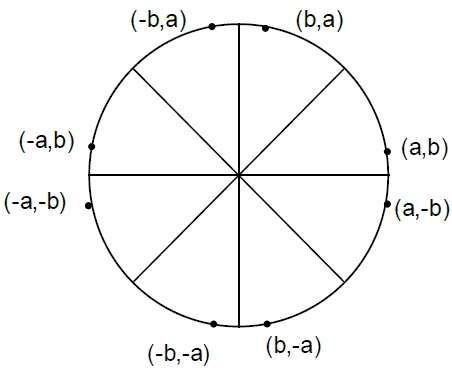
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Algorithme du point médian

Step 1 - Rayon d'entrée r et le centre du cercle $ (x_ {c,} y_ {c}) $ et obtenez le premier point sur la circonférence du cercle centré sur l'origine comme

(x0, y0) = (0, r)

Step 2 - Calculer la valeur initiale du paramètre de décision comme

$ P_ {0} $ = 5/4 - r (Voir la description suivante pour simplifier cette équation.)

f(x, y) = x2 + y2 - r2 = 0

f(xi - 1/2 + e, yi + 1)
        = (xi - 1/2 + e)2 + (yi + 1)2 - r2 
        = (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
        = f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0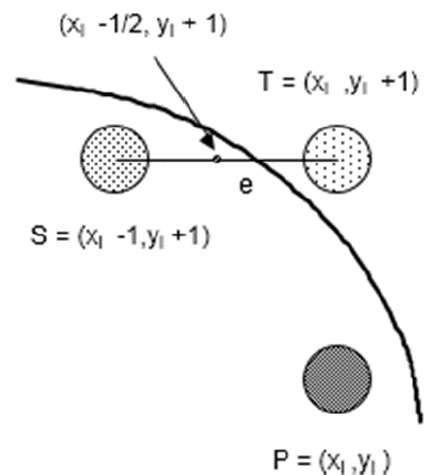

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,

If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1    = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
        = di - 2(xi - 1) + 2(yi + 1) + 1
        = di + 2(yi + 1 - xi + 1) + 1
		  
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
   di+1 = f(xi - 1/2, yi + 1 + 1)
       = di + 2yi+1 + 1
		  
The initial value of di is
   d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (xi - 1, yi + 1) is chosen then
   di+1 = di + -2xi+1 + 2yi+1 + 1
	
When point T = (xi, yi + 1) is chosen then
   di+1 = di + 2yi+1 + 1

Step 3 - A chaque position $ X_ {K} $ commençant à K = 0, effectuez le test suivant -

If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
   PK+1 = PK + 2XK+1 + 1
Else
   PK+1 = PK + 2XK+1 + 1 – 2YK+1
	
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.

Step 4 - Déterminez les points de symétrie dans sept autres octants.

Step 5 - Déplacez chaque position de pixel calculée (X, Y) sur le chemin circulaire centré sur $ (X_ {C,} Y_ {C}) $ et tracez les valeurs des coordonnées.

X = X + XC,   Y = Y + YC

Step 6 - Répétez les étapes 3 à 5 jusqu'à X> = Y.