ग्राफ सिद्धांत - कनेक्टिविटी
क्या एक ग्राफ को एक शीर्ष से दूसरे तक पहुंचाना संभव है, यह निर्धारित किया जाता है कि ग्राफ़ कैसे जुड़ा है। ग्राफ थ्योरी में कनेक्टिविटी एक मूल अवधारणा है। कनेक्टिविटी परिभाषित करती है कि क्या ग्राफ़ जुड़ा हुआ है या डिस्कनेक्ट किया गया है। इसमें किनारे और वर्टेक्स के आधार पर सबटॉपिक्स हैं, जिन्हें एज कनेक्टिविटी और वर्टेक्स कनेक्टिविटी के रूप में जाना जाता है। आइए हम उनके बारे में विस्तार से चर्चा करें।
कनेक्टिविटी
एक ग्राफ कहा जाता है connected if there is a path between every pair of vertex। प्रत्येक शीर्ष से किसी भी अन्य शीर्ष पर, कुछ मार्ग को पार करने के लिए होना चाहिए। इसे एक ग्राफ की कनेक्टिविटी कहा जाता है। कई डिस्कनेक्ट किए गए कोने और किनारों के साथ एक ग्राफ को डिस्कनेक्ट करने के लिए कहा जाता है।
Example 1
निम्नलिखित ग्राफ में, एक शीर्ष से किसी अन्य शीर्ष पर यात्रा करना संभव है। उदाहरण के लिए, व्यक्ति 'ab-e' पथ का उपयोग करके 'a' से 'vertex' तक पहुँच सकता है।
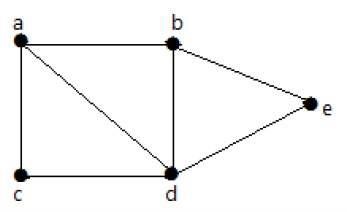
Example 2
निम्नलिखित उदाहरण में, शीर्ष से 'ए' से 'वर्टेक्स' एफ 'तक ट्रेस करना संभव नहीं है क्योंकि उनके बीच प्रत्यक्ष या अप्रत्यक्ष रूप से कोई रास्ता नहीं है। इसलिए यह एक डिस्कनेक्ट ग्राफ है।
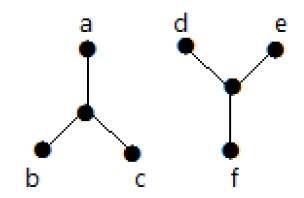
कट वर्टेक्स
'G' को एक कनेक्टेड ग्राफ होने दें। एक वर्टेक्स V is G को 'G' का कट वर्टेक्स कहा जाता है, यदि 'G-V' ('G' से 'V' हटाएं) के परिणाम डिस्कनेक्ट हो जाते हैं। एक ग्राफ से कटा हुआ शीर्ष हटाने से इसे दो या दो से अधिक ग्राफ़ में तोड़ दिया जाता है।
Note - कटी हुई चोटी को हटाने से एक ग्राफ काट दिया जा सकता है।
कनेक्टेड ग्राफ 'जी' में अधिकतम (n-2) कटे हुए कोने हो सकते हैं।
Example
निम्नलिखित ग्राफ में, 'ई' और 'सी' कटे हुए कोने हैं।

Will e ’या 'c’ को हटाने से ग्राफ डिसकनेक्टेड ग्राफ बन जाएगा।

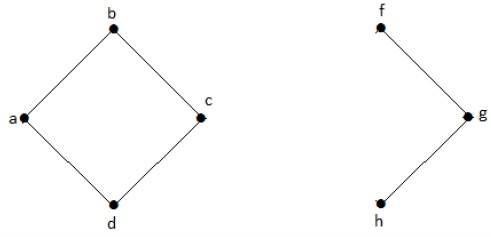
Without जी ’के बिना, वर्टेक्स and सी’ और वर्टेक्स and एच ’और कई अन्य के बीच कोई रास्ता नहीं है। इसलिए यह कट ईट के साथ 'ई' के रूप में डिस्कनेक्ट किया गया ग्राफ़ है। इसी प्रकार, 'ग' भी उपरोक्त ग्राफ के लिए एक कटा हुआ शीर्ष है।
कट एज (पुल)
'G' को एक कनेक्टेड ग्राफ होने दें। यदि 'G-e' डिस्कनेक्ट किए गए ग्राफ़ में परिणामित होता है, तो एक धार 'e' is G को कट एज कहा जाता है।
यदि किसी ग्राफ़ में किसी किनारे को हटाने से दो या दो से अधिक ग्राफ़ निकलते हैं, तो उस किनारे को कट एज कहा जाता है।
Example
निम्नलिखित ग्राफ में, कट किनारे [(सी, ई)] है।

ग्राफ से किनारे (सी, ई) को हटाकर, यह डिस्कनेक्ट किया गया ग्राफ बन जाता है।


उपरोक्त ग्राफ़ में, किनारे (सी, ई) को हटाने से ग्राफ़ दो में टूट जाता है जो डिस्कनेक्ट किए गए ग्राफ़ के अलावा कुछ भी नहीं है। इसलिए, बढ़त (c, e) ग्राफ का एक कटा हुआ किनारा है।
Note - 'G' को 'n' वर्टिक्स के साथ जुड़ा हुआ ग्राफ माना जाता है
कट एज ई if जी अगर और केवल अगर धार 'ई' जी में किसी भी चक्र का हिस्सा नहीं है।
कटे हुए किनारों की अधिकतम संख्या संभव है 'एन -1'।
जब भी कटे हुए किनारे मौजूद होते हैं, तो कटे हुए कोने भी मौजूद होते हैं क्योंकि कटे हुए किनारे का कम से कम एक शीर्ष कटे हुए शीर्ष वाला होता है।
यदि एक कट वर्टेक्स मौजूद है, तो एक कट एज मौजूद हो सकता है या नहीं।
ग्राफ का कट सेट
'G' = (V, E) को एक जुड़ा हुआ ग्राफ होने दें। E के एक उपसमूह E को G का कट सेट कहा जाता है यदि G से E के सभी किनारों को हटा दिया जाए तो G डिस्कनेक्ट हो जाता है।
यदि किसी ग्राफ से किनारों की एक निश्चित संख्या को हटाने से यह डिस्कनेक्ट हो जाता है, तो उन हटाए गए किनारों को ग्राफ का कट सेट कहा जाता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें। इसका कट सेट E1 = {e1, e3, e5, e8} है।
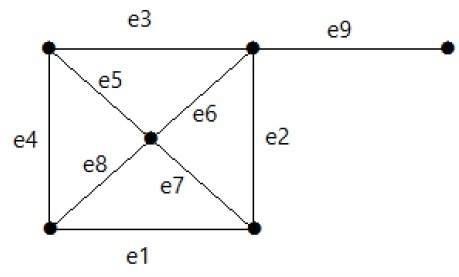
ग्राफ से कट सेट E1 को हटाने के बाद, यह निम्नानुसार दिखाई देगा -
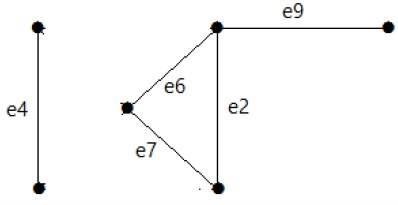
इसी तरह, अन्य कट सेट हैं जो ग्राफ़ को डिस्कनेक्ट कर सकते हैं -
E3 = {e9} - ग्राफ़ का सबसे छोटा कट सेट।
E4 = {e3, e4, e5}
एज कनेक्टिविटी
'G' को एक कनेक्टेड ग्राफ होने दें। किनारों की न्यूनतम संख्या जिसका निष्कासन 'G' काटता है, को G की किनारे कनेक्टिविटी कहा जाता है।
Notation - Iλ (G)
दूसरे शब्दों में, number of edges in a smallest cut set of G को G की एज कनेक्टिविटी कहा जाता है।
यदि 'G' में एक कट एज है, तो λ (G) 1. है (G. की बढ़त कनेक्टिविटी)
Example
निम्नलिखित ग्राफ पर एक नज़र डालें। दो न्यूनतम किनारों को हटाने से, जुड़ा हुआ ग्राफ डिस्कनेक्ट हो जाता है। इसलिए, इसका एज कनेक्टिविटी (λ (G)) 2 है।
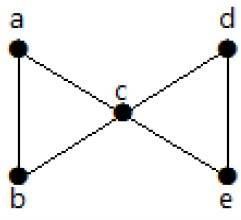
यहां दो किनारों को हटाकर ग्राफ को डिस्कनेक्ट करने के चार तरीके दिए गए हैं -

वर्टेक्स कनेक्टिविटी
'G' को एक कनेक्टेड ग्राफ होने दें। उन लंबों की न्यूनतम संख्या जिनके निष्कासन से 'G' या तो डिस्कनेक्ट हो जाता है या एक तुच्छ ग्राफ में 'G' को कम कर देता है, इसे अपनी शीर्ष कनेक्टिविटी कहा जाता है।
Notation - के (जी)
Example
उपरोक्त ग्राफ में, 'ई' और 'आई' को हटाकर ग्राफ को डिस्कनेक्ट कर दिया गया है।

यदि जी में एक कट वर्टेक्स है, तो K (G) = 1।
Notation - किसी भी जुड़े ग्राफ G के लिए,
K (G) λ λ (G) δ ≤ (G)
वर्टेक्स कनेक्टिविटी (K (G)), एज कनेक्टिविटी (λ (G)), G () (G)) की न्यूनतम संख्या।
Example
निम्नलिखित ग्राफ के लिए λ (G) और K (G) की गणना करें -
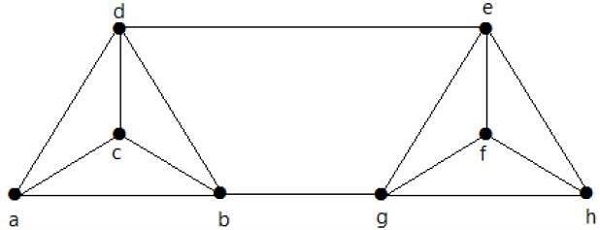
Solution
ग्राफ से,
= (जी) = 3
K (G) (λ (G) δ ≤ (G) = 3 (1)
के (जी) (2 (2)
किनारों को हटाना {d, e} और {b, h}, हम G को डिस्कनेक्ट कर सकते हैं।
इसलिए,
λ (जी) = 2
2 δ λ (G) ≤ ≤ (G) = 2 (3)
से (2) और (3), वर्टेक्स कनेक्टिविटी K (G) = 2