ग्राफ सिद्धांत - समसामयिकता
एक ग्राफ विभिन्न रूपों में मौजूद हो सकता है, जिसमें एक ही संख्या में कोने, किनारे और एक ही किनारे की कनेक्टिविटी हो। ऐसे ग्राफ को आइसोमॉर्फिक ग्राफ कहा जाता है। ध्यान दें कि हम इस अध्याय में ग्राफ़ को मुख्य रूप से उन्हें संदर्भित करने और उन्हें एक दूसरे से पहचानने के उद्देश्य से लेबल करते हैं।
आइसोमोर्फिक रेखांकन
दो ग्राफ G 1 और G 2 को आइसोमोर्फिक कहा जाता है यदि -
उनके घटकों की संख्या (कोने और किनारे) समान हैं।
उनकी बढ़त कनेक्टिविटी बरकरार है।
Note- संक्षेप में, दो आइसोमॉर्फिक ग्राफ़ों में से, एक दूसरे का एक संपादित संस्करण है। एक अनलेबल ग्राफ को एक आइसोमॉर्फिक ग्राफ के रूप में भी सोचा जा सकता है।
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
यदि जी 1 G जी 2 तो -
| वी (जी 1 ) | = | वी (जी 2 ) |
| ई (जी 1 ) | = | ई (जी 2 ) |
जी 1 और जी 2 के डिग्री अनुक्रम समान हैं।
यदि कोने {V 1 , V 2 , .. Vk} G 1 में लंबाई K का एक चक्र बनाते हैं , तो कोने {f (V 1 ), f (V 2 ),… f (Vk)} को एक चक्र बनाना चाहिए। जी 2 में लंबाई के ।
उपरोक्त सभी स्थितियां ग्राफ 1 और G 2 के लिए आइसोमोर्फिक होना आवश्यक हैं , लेकिन यह साबित करने के लिए पर्याप्त नहीं है कि ग्राफ आइसोमॉर्फिक हैं।
(G 1 G G 2 ) यदि और केवल अगर (G 1 - - G 2 -) जहां G 1 और G 2 सरल रेखांकन हैं।
(G 1 G G 2 ) यदि G 1 और G 2 के आसन्न मैट्रिक्स समान हैं।
(G 1 G G 2 ) यदि और केवल यदि G 1 और G 2 के संगत उपसमूह (G1 में कुछ कोने हटाकर और ग्राफ G 2 में उनकी छवियां ) समद्विभाजक हैं।
Example
निम्नलिखित में से कौन सा ग्राफ आइसोमॉर्फिक है?
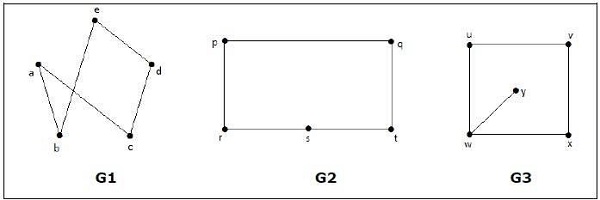
ग्राफ जी 3 में , वर्टेक्स 'डब्ल्यू' में केवल डिग्री 3 है, जबकि अन्य सभी ग्राफ वर्टिकल में डिग्री 2 है। इसलिए जी 3 आइसोमॉर्फिक से जी 1 या जी 2 नहीं है ।
जी 1 और जी 2 के पूरक लेना , आपके पास है -
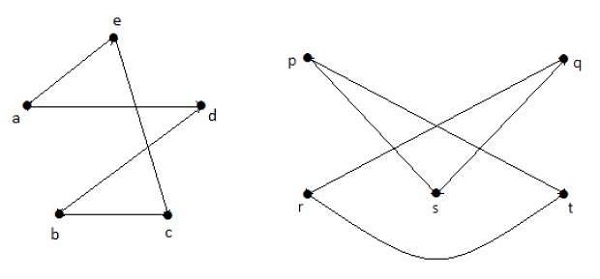
यहां, (जी 1 - 2 जी 2 -), इसलिए (जी 1 ) जी 2 )।
प्लेनर रेखांकन
एक ग्राफ 'जी' को प्लेनर कहा जाता है यदि इसे एक विमान या एक गोले पर खींचा जा सकता है ताकि कोई भी दो किनारे एक-दूसरे को एक गैर-शीर्ष बिंदु पर पार न करें।
Example
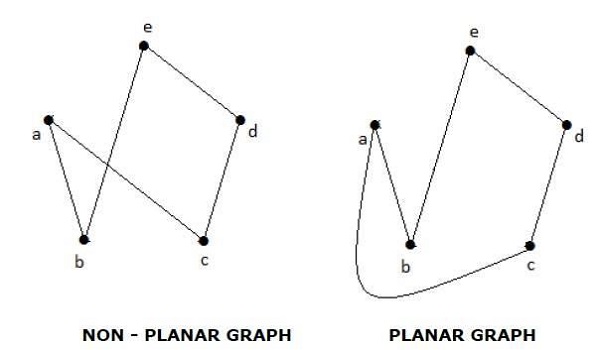
क्षेत्रों
प्रत्येक प्लानर ग्राफ विमान को संबंधित क्षेत्रों में विभाजित करता है जिसे क्षेत्र कहते हैं।
Example
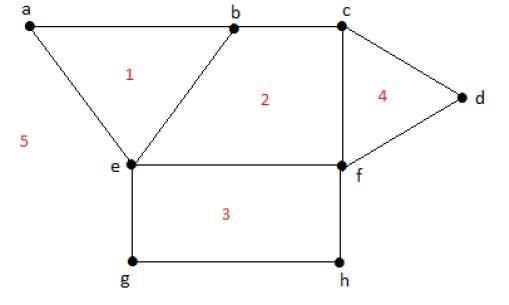
एक बंधे हुए क्षेत्र की डिग्री r = deg(r) क्षेत्रों को घेरने वाले किनारों की संख्या r।
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8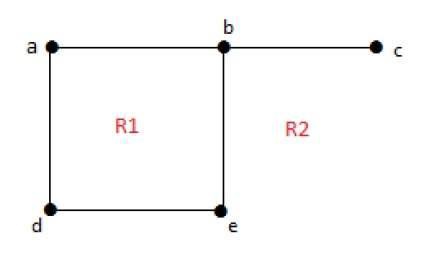
एक अनबिके क्षेत्र की डिग्री r = deg(r) क्षेत्रों को घेरने वाले किनारों की संख्या r।
deg(R1) = 4
deg(R2) = 6प्लानर रेखांकन में, निम्नलिखित गुण अच्छे हैं -
'N' वर्टिकल के साथ एक प्लैनर ग्राफ में, सभी वर्टिकल की डिग्री का योग है -
इसके अनुसार Sum of Degrees of Regions/ प्रमेय, 'एन' क्षेत्रों के साथ एक प्लैनर ग्राफ में, क्षेत्रों की डिग्री का योग है -
उपरोक्त प्रमेय के आधार पर, आप निम्नलिखित निष्कर्ष निकाल सकते हैं -
एक प्लैनर ग्राफ में,
यदि प्रत्येक क्षेत्र की डिग्री K है, तो क्षेत्रों की डिग्री का योग है -
यदि प्रत्येक क्षेत्र की डिग्री कम से कम K (, K) है, तो
यदि प्रत्येक क्षेत्र की डिग्री अधिकांश K (, K) पर है, तो
Note - मान लें कि सभी क्षेत्रों में समान डिग्री है।
इसके अनुसार Euler’s Formulae प्लानर ग्राफ पर,
यदि एक ग्राफ 'जी' जुड़ा हुआ प्लानर है, तो
यदि 'के' घटकों के साथ एक प्लैनर ग्राफ, तो
जहाँ, | वी | वर्टिकल की संख्या है, | E | किनारों की संख्या है, और | R | क्षेत्रों की संख्या है।
एज वर्टेक्स असमानता
यदि 'G' कम से कम 'K' में प्रत्येक क्षेत्र की डिग्री के साथ जुड़ा हुआ प्लानर ग्राफ है,
| E | ≤ के / / (के -2) {| v | - 2}
तुम्हें पता है, | वी | + | आर | = | ई | + 2
लालकृष्ण | R | | 2 | ई |
K (| E | - | V | + 2) E 2 | E |
(के - 2) | ई | ≤ K (| V | - 2)
| E | ≤ के / / (के -2) {| v | - 2}
यदि 'G' एक साधारण जुड़ा हुआ प्लानर ग्राफ है, तो
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4कम से कम एक वर्टेक्स V • at G मौजूद है, जैसे कि नीचे (V) ver 5।
यदि 'G' एक साधारण जुड़ा हुआ प्लानर ग्राफ है (कम से कम 2 किनारों वाला) और कोई त्रिकोण नहीं है, तो
|E| ≤ {2|V| – 4}Kuratowski के प्रमेय
एक ग्राफ 'जी' नॉन-प्लानर है अगर और केवल अगर 'जी' में एक सबग्राफ है जो कि केओएम 5 या के 3,3 के लिए होमोमोर्फिक है ।
समरूपता
दो ग्राफ G 1 और G 2 को होमोमोर्फिक कहा जाता है, अगर इनमें से प्रत्येक ग्राफ को G के कुछ किनारों को अधिक चक्कर लगाकर एक ही ग्राफ 'G' से प्राप्त किया जा सकता है। निम्नलिखित उदाहरण पर एक नज़र डालें -

एक वर्टेक्स जोड़कर किनारे 'आरएस' को दो किनारों में विभाजित करें।
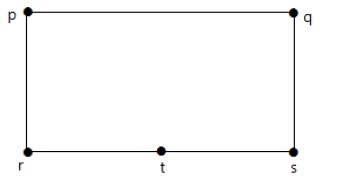
नीचे दिखाए गए रेखांकन पहले ग्राफ के समरूप हैं।
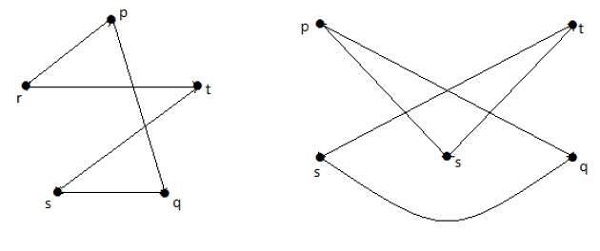
यदि जी 1 , जी 2 से आइसोमोर्फिक है , तो जी, जी 2 के लिए होमियोमॉर्फिक है, लेकिन ऐंठन की आवश्यकता सच नहीं है।
4 या उससे कम लम्बाई वाला कोई भी ग्राफ़ प्लानर है।
8 या उससे कम किनारों वाला कोई भी ग्राफ़ प्लानर है।
एक पूरा ग्राफ K n प्लानर है अगर और केवल अगर n is 4।
पूरा द्विदलीय ग्राफ K m, n प्लानेर है और यदि केवल ≤ 2 या n। 2 है तो।
न्यूनतम संख्या के साथ एक साधारण गैर-प्लानर ग्राफ पूरा ग्राफ K 5 है ।
न्यूनतम संख्या किनारों के साथ सरल गैर-प्लानर ग्राफ K 3, 3 है ।
पॉलीहेड्रल ग्राफ
एक साधारण कनेक्टेड प्लानर ग्राफ को पॉलीहेड्रल ग्राफ कहा जाता है यदि प्रत्येक वर्टेक्स की डिग्री, 3 है, यानी, deg (V) V 3 ∈ V ∈ जी।
3 | वी | | 2 | ई |
3 | R | | 2 | ई |