ग्राफ सिद्धांत - त्वरित गाइड
गणित और कंप्यूटर विज्ञान के क्षेत्र में, ग्राफ सिद्धांत ग्राफ़ का अध्ययन है जो किनारों और कोने के बीच के रिश्ते से चिंतित है । यह कंप्यूटर विज्ञान, सूचना प्रौद्योगिकी, जैव विज्ञान, गणित और भाषा विज्ञान में कुछ नाम रखने के लिए एक लोकप्रिय विषय है। आगे की हलचल के बिना, हम एक ग्राफ को परिभाषित करने के साथ शुरू करते हैं।
ग्राफ़ क्या है?
एक ग्राफ वस्तुओं के एक सेट का एक चित्रमय प्रतिनिधित्व है जहां कुछ जोड़े वस्तुओं के लिंक से जुड़े होते हैं। परस्पर जुड़ी वस्तुओं को ऐसे बिंदुओं द्वारा दर्शाया जाता है जिन्हें कहा जाता हैvertices, और कड़ियों को जोड़ने वाले लिंक को कहा जाता है edges।
औपचारिक रूप से, एक ग्राफ सेट की एक जोड़ी है (V, E), कहाँ पे Vकोने का सेट है और E किनारों का सेट है, जोडों के जोड़े को जोड़ता है। निम्नलिखित ग्राफ पर एक नज़र डालें -
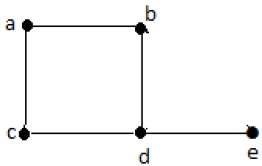
उपरोक्त ग्राफ में,
वी = {ए, बी, सी, डी, ई}
E = {अब, एसी, बीडी, सीडी, डे}
ग्राफ थ्योरी के अनुप्रयोग
ग्राफ सिद्धांत के इंजीनियरिंग के विभिन्न क्षेत्रों में इसके अनुप्रयोग हैं -
Electrical Engineering- ग्राफिकल थ्योरी की अवधारणाओं का उपयोग सर्किट कनेक्शन डिजाइन करने में बड़े पैमाने पर किया जाता है। कनेक्शन के प्रकार या संगठन को टोपोलॉजी के रूप में नामित किया गया है। टोपोलॉजी के लिए कुछ उदाहरण स्टार, पुल, श्रृंखला और समानांतर टोपोलॉजी हैं।
Computer Science- ग्राफ थ्योरी का उपयोग एल्गोरिदम के अध्ययन के लिए किया जाता है। उदाहरण के लिए,
- क्रुस्कल का एल्गोरिदम
- प्राइम का एल्गोरिथम
- डीजकस्ट्रा का एल्गोरिथम
Computer Network - नेटवर्क में इंटरकनेक्टेड कंप्यूटरों के बीच संबंध ग्राफ सिद्धांत के सिद्धांतों का अनुसरण करते हैं।
Science - किसी पदार्थ की आणविक संरचना और रासायनिक संरचना, किसी जीव की डीएनए संरचना आदि को रेखांकन द्वारा दर्शाया जाता है।
Linguistics - किसी भाषा का पेड़ और किसी भाषा का व्याकरण रेखांकन का उपयोग करता है।
General- शहरों के बीच के मार्गों को रेखांकन के उपयोग से दर्शाया जा सकता है। पदानुक्रमित आदेश की जानकारी जैसे परिवार के पेड़ को एक विशेष प्रकार के ग्राफ के रूप में इस्तेमाल किया जा सकता है।
एक ग्राफ़ बिंदुओं और बिंदुओं से जुड़ी रेखाओं का आरेख है। इसमें कम से कम एक लाइन होती है जो दो वर्टीकल के सेट से जुड़ती है जिसमें कोई भी शीर्ष नहीं होता है। ग्राफ सिद्धांत में रेखांकन की अवधारणा कुछ मूल शर्तों पर खड़ी होती है जैसे बिंदु, रेखा, शीर्ष, किनारे, कोणों की डिग्री, रेखांकन के गुण इत्यादि। इस अध्याय में, हम ग्राफ सिद्धांत के इन मूल सिद्धांतों को शामिल करेंगे।
बिंदु
A pointएक आयामी, दो आयामी या तीन आयामी अंतरिक्ष में एक विशेष स्थिति है। बेहतर समझ के लिए, एक बिंदु को एक वर्णमाला द्वारा निरूपित किया जा सकता है। इसे डॉट के साथ दर्शाया जा सकता है।
उदाहरण

यहाँ, बिंदु 'a' नाम का एक बिंदु है।
लाइन
ए Lineदो बिंदुओं के बीच एक संबंध है। इसे एक ठोस रेखा के साथ दर्शाया जा सकता है।
Example

यहाँ, 'ए' और 'बी' अंक हैं। इन दोनों बिंदुओं के बीच की कड़ी को रेखा कहते हैं।
शिखर
एक शीर्ष बिंदु एक बिंदु है जहां कई लाइनें मिलती हैं। इसे ए भी कहा जाता हैnode। बिंदुओं के समान, एक वर्णमाला भी एक वर्णमाला द्वारा निरूपित की जाती है।
Example

यहां, शीर्ष को वर्णमाला 'ए' नाम दिया गया है।
एज
एक किनारे एक रेखा के लिए गणितीय शब्द है जो दो कोने जोड़ता है। एक किनारे से कई किनारों का निर्माण किया जा सकता है। एक शीर्ष के बिना, एक किनारे का गठन नहीं किया जा सकता है। एक आरंभिक शीर्ष और एक छोर के लिए एक अंतिम शीर्ष होना चाहिए।
Example

यहाँ, 'a' और 'b' दो कोने हैं और उनके बीच की कड़ी को किनारे कहा जाता है।
ग्राफ़
एक ग्राफ 'जी' को जी = (वी, ई) के रूप में परिभाषित किया गया है, जहां वी सभी लंबों का एक सेट है और ई ग्राफ में सभी किनारों का एक सेट है।
Example 1

उपरोक्त उदाहरण में, ab, ac, cd, और bd ग्राफ के किनारे हैं। इसी तरह, ए, बी, सी और डी ग्राफ के कोने हैं।
Example 2
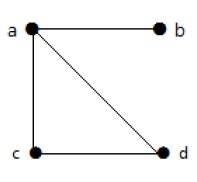
इस ग्राफ में, चार कोने a, b, c, और d हैं, और चार किनारों ab, ac, ad, और cd हैं।
लूप
ग्राफ में, यदि एक किनारे को शीर्ष से स्वयं तक खींचा जाता है, तो इसे लूप कहा जाता है।
Example 1

उपर्युक्त ग्राफ में, वी एक शीर्ष है जिसके लिए एक छोर (वी, वी) एक लूप बनाता है।
Example 2

इस ग्राफ में, दो छोरें हैं जो वर्टेक्स ए, और वर्टेक्स बी पर बनती हैं।
वर्टेक्स की डिग्री
यह वर्टेक्स V से सटे कोने की संख्या है।
Notation - deg (V)।
किसी भी कोने की डिग्री के साथ सरल ग्राफ में, किसी भी कोने की डिग्री है -
deg (v) - n - 1 v v ≤ जी
एक शीर्ष अपने आप को छोड़कर सभी अन्य कोने के साथ एक बढ़त बना सकता है। तो एक शीर्ष की डिग्री तक हो जाएगाnumber of vertices in the graph minus 1। यह 1 स्वयं-शीर्ष के लिए है क्योंकि यह स्वयं से लूप नहीं बना सकता है। यदि किसी भी कोने पर एक लूप है, तो यह एक सरल ग्राफ़ नहीं है।
ग्राफ के दो मामलों के तहत शीर्ष की डिग्री पर विचार किया जा सकता है -
अप्रत्यक्ष ग्राफ़
निर्देशित आलेख
अप्रत्यक्ष ग्राफ़ में वर्टेक्स की डिग्री
एक अप्रत्यक्ष ग्राफ़ में कोई निर्देशित किनारा नहीं है। निम्नलिखित उदाहरणों पर विचार करें।
Example 1
निम्नलिखित ग्राफ पर एक नज़र डालें -

उपरोक्त अप्रत्यक्ष ग्राफ़ में,
नीचे (ए) = 2, क्योंकि शीर्ष पर 2 किनारों की बैठक 'a' है।
deg (b) = 3, क्योंकि शीर्ष पर 3 किनारों की बैठकें 'b' हैं।
नीचे (c) = 1, क्योंकि शीर्ष पर 1 किनारे का गठन 'c' है
तो 'ग' एक है pendent vertex।
नीचे (d) = 2, क्योंकि शीर्ष पर 2 किनारों की बैठक 'd' है।
deg (e) = 0, क्योंकि शीर्ष पर 'e' में 0 किनारे बने होते हैं।
तो 'ई' एक है isolated vertex।
Example 2
निम्नलिखित ग्राफ पर एक नज़र डालें -

उपरोक्त ग्राफ में,
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2, and deg (e) = 0)।
शीर्ष 'ई ’एक पृथक शीर्ष है। ग्राफ में कोई पेंडेंट शीर्ष नहीं है।
एक निर्देशित ग्राफ में वर्टेक्स की डिग्री
एक निर्देशित ग्राफ में, प्रत्येक शीर्ष पर एक है indegree और एक outdegree।
एक ग्राफ की Indegree
वर्टेक्स V का इंडेग्री, किनारों की संख्या है जो वर्टेक्स V में आ रहे हैं।
Notation - deg - (V)।
एक रेखांकन की रूपरेखा
वर्टेक्स V का आउटड्री, किनारों की संख्या है जो वर्टेक्स V से निकल रहे हैं।
Notation - deg + (V)।
निम्नलिखित उदाहरणों पर विचार करें।
Example 1
निम्नलिखित निर्देशित ग्राफ पर एक नज़र डालें। वर्टेक्स 'ए' के दो किनारे हैं, 'ऐड' और 'एब', जो बाहर की ओर जा रहे हैं। इसलिए इसकी रूपरेखा 2 है। इसी प्रकार, एक किनारे 'गा' है, जो 'a' की ओर आ रहा है। अत: 'a' की इंद्री 1 है।

अन्य शीर्षकों की इंद्री और आउटड्री निम्नलिखित तालिका में दिखाए गए हैं -
| शिखर | Indegree | Outdegree |
|---|---|---|
| ए | 1 | 2 |
| ख | 2 | 0 |
| सी | 2 | 1 |
| घ | 1 | 1 |
| इ | 1 | 1 |
| च | 1 | 1 |
| जी | 0 | 2 |
Example 2
निम्नलिखित निर्देशित ग्राफ पर एक नज़र डालें। वर्टेक्स going ए ’में 'ए’ की बढ़त होती है जो वर्टेक्स' ए ’से बाहर की ओर जाती है। इसलिए इसकी रूपरेखा 1 है। इसी तरह, ग्राफ में बढ़त 'बा' है जो 'शीर्ष' की ओर आ रही है। अत: 'a' की इंद्री 1 है।

अन्य शीर्षकों की इंद्री और आउटड्री निम्नलिखित तालिका में दिखाए गए हैं -
| शिखर | Indegree | Outdegree |
|---|---|---|
| ए | 1 | 1 |
| ख | 0 | 2 |
| सी | 2 | 0 |
| घ | 1 | 1 |
| इ | 1 | 1 |
पेंडेंट वर्टेक्स
एक वर्टेक्स की डिग्री का उपयोग करके, हमारे पास दो विशेष प्रकार के कोने हैं। डिग्री एक के साथ एक शीर्ष को पेंडेंट शीर्ष कहा जाता है।
Example

यहाँ, इस उदाहरण में, वर्टेक्स 'ए' और वर्टेक्स 'बी' का कनेक्टेड एज 'एब' है। तो 'a ’के संबंध में, b b’ की ओर केवल एक किनारा है और इसी तरह' b ’के संबंध में, 'a’ के संबंध में केवल एक ही छोर है, tex a ’के लिए केवल एक किनारे है। अंत में, वर्टेक्स 'ए' और वर्टेक्स 'बी' के पास एक डिग्री है जिसे पेंडेंट वर्टेक्स भी कहा जाता है।
अलग-थलग
डिग्री शून्य के साथ एक शीर्ष को एक पृथक शीर्ष कहा जाता है।
Example

यहाँ, शीर्ष 'a' और vertex 'b' की आपस में कोई कनेक्टिविटी नहीं है और किसी अन्य कोने में भी है। अतः '' ए 'और' बी 'दोनों के अंश शून्य हैं। इन्हें पृथक खण्ड भी कहा जाता है।
समीपता
यहाँ आसन्न के मानदंड हैं -
एक रेखांकन में, दो सिरों को कहा जाता है adjacent, अगर दो कोने के बीच एक धार है। यहाँ, उन दो सिरों को जोड़ने वाले एकल किनारे द्वारा कोने की आसन्नता बनाए रखी जाती है।
एक ग्राफ़ में, दो किनारों को आसन्न कहा जाता है, अगर दो किनारों के बीच एक सामान्य शीर्ष है। यहां, किनारों की निकटता को एकल शीर्ष द्वारा बनाए रखा जाता है जो दो किनारों को जोड़ रहा है।
Example 1
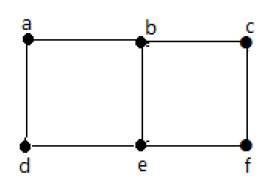
उपरोक्त ग्राफ में -
'a' और 'b' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'ab' है।
'a' और 'd' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'विज्ञापन' है।
ab 'और' be 'आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष' b 'है।
होना 'और' डे 'आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष' ई 'है।
Example 2
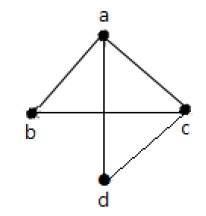
उपरोक्त ग्राफ में -
'a' और 'd' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'विज्ञापन' है।
'c' और 'b' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'cb' है।
'विज्ञापन' और 'सीडी' आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष 'डी' है।
'एसी' और 'सीडी' आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष 'सी' है।
समानांतर किनारे
एक ग्राफ में, यदि एक जोड़े को एक से अधिक किनारों से जोड़ा जाता है, तो उन किनारों को समानांतर किनारे कहा जाता है।
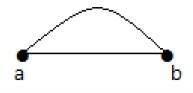
उपर्युक्त ग्राफ में, 'a' और 'b' दो कोने हैं जो उनके बीच दो किनारों 'ab' और 'ab' से जुड़े हैं। तो यह एक समानांतर किनारे के रूप में कहा जाता है।
मल्टी ग्राफ
समानांतर किनारों वाले एक ग्राफ को मल्टीग्राफ के रूप में जाना जाता है।
Example 1

उपर्युक्त ग्राफ में, पाँच किनारे हैं 'अब', 'एसी', 'सीडी', 'सीडी' और 'बीडी'। चूँकि 'c' और 'd' के बीच दो समानांतर किनारे हैं, यह एक मल्टीग्राफ है।
Example 2
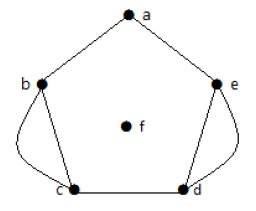
उपरोक्त ग्राफ में, 'बी' और 'सी' के दो किनारे हैं। शीर्ष 'ई' और 'डी' के बीच भी दो किनारे हैं। इसलिए यह एक मल्टीग्राफ है।
एक ग्राफ की डिग्री अनुक्रम
यदि किसी ग्राफ में सभी कोणों की डिग्री को अवरोही या आरोही क्रम में व्यवस्थित किया जाता है, तो प्राप्त अनुक्रम को ग्राफ के डिग्री अनुक्रम के रूप में जाना जाता है।
Example 1

| शिखर | ए | ख | सी | घ | इ |
|---|---|---|---|---|---|
| को जोड़ रहा | बी, सी | ए, डी | ए, डी | सी, बी, ई | घ |
| डिग्री | 2 | 2 | 2 | 3 | 1 |
ऊपर के ग्राफ़ में, कोने {d, a, b, c, e} के लिए, डिग्री अनुक्रम {3, 2, 2, 2, 1} है।
Example 2

| शिखर | ए | ख | सी | घ | इ | च |
|---|---|---|---|---|---|---|
| को जोड़ रहा | ख, ई | एसी | बी, डी | सी, ई | ए, डी | - |
| डिग्री | 2 | 2 | 2 | 2 | 2 | 0 |
उपरोक्त ग्राफ में, कोने {{a, b, c, d, e, f} के लिए, डिग्री अनुक्रम {2, 2, 2, 2, 2, 2, 0} है।
रेखांकन विभिन्न गुणों के साथ आते हैं जो उनकी संरचनाओं के आधार पर रेखांकन के लक्षण वर्णन के लिए उपयोग किए जाते हैं। इन गुणों को ग्राफ सिद्धांत के क्षेत्र से संबंधित विशिष्ट शब्दों में परिभाषित किया गया है। इस अध्याय में, हम कुछ मूल गुणों पर चर्चा करेंगे जो सभी ग्राफ़ में सामान्य हैं।
दो कार्यक्षेत्रों के बीच की दूरी
यह वर्टेक्स यू और वर्टेक्स वी के बीच सबसे छोटे रास्ते में किनारों की संख्या है। यदि दो कोने को जोड़ने वाले कई मार्ग हैं, तो सबसे छोटे मार्ग को दो कोने के बीच की दूरी के रूप में माना जाता है।
संकेतन - d (U, V)
एक शीर्ष से दूसरे तक मौजूद पथों की संख्या हो सकती है। उनमें से, आपको केवल सबसे छोटा एक चुनने की आवश्यकता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -

यहाँ, वर्टिक्स 'd' से वर्टेक्स 'e' या बस 'de' की दूरी 1 है क्योंकि उनके बीच एक किनारे है। वर्टेक्स 'd' से वर्टेक्स 'e' तक कई रास्ते हैं -
- दा, अब, हो
- डीएफ, एफजी, जीई
- डी (यह कोने के बीच की दूरी के लिए माना जाता है)
- df, fc, ca, ab, होना
- दा, एसी, सीएफ, एफजी, जीई
एक वर्टेक्स की विलक्षणता
सभी शीर्षों के लिए एक शीर्ष के बीच की अधिकतम दूरी को शीर्ष के विलक्षणता के रूप में माना जाता है।
संकेतन - e (V)
ग्राफ में एक विशेष शीर्ष से दूसरे सभी शीर्षों की दूरी को लिया जाता है और उन दूरी के बीच, विलक्षणता सबसे अधिक दूरी है।
Example
उपर्युक्त ग्राफ में, 'a' की विलक्षणता 3 है।
'A' से 'b' की दूरी 1 ('ab') है,
'a' से 'c' 1 है ('ac'),
'a' से 'd' 1 है ('ad'),
'a' से 'e' 2 है ('ab' - 'be') या ('ad' - 'de'))
'a' से 'f' 2 है ('ac' - 'cf') या ('ad' - 'df'),
'a' से 'g' 3 है ('ac' - 'cf' - 'fg') या ('ad' - 'df' - 'fg')।
तो सनकीपन 3 है, जो कि 'अग' के बीच की दूरी से 'क' से अधिकतम है जो अधिकतम है।
दूसरे शब्दों में,
e (b) = 3
e (c) = 3
e (d) = 2
e (e) = 3
e (f) = 3
e (g) = 3
कनेक्टेड ग्राफ़ का त्रिज्या
सभी चक्करों में से न्यूनतम विलक्षणता को ग्राफ जी की त्रिज्या के रूप में माना जाता है। सभी शीर्षों के बीच की सभी दूरीों के बीच की अधिकतम दूरी को ग्राफ जी की त्रिज्या माना जाता है।
संकेतन - r (G)
एक ग्राफ में कोने की सभी विलक्षणताओं से, जुड़े हुए ग्राफ की त्रिज्या उन सभी विलक्षणताओं में से न्यूनतम है।
Example
उपरोक्त ग्राफ r (G) = 2 में, जो 'd' के लिए न्यूनतम विलक्षणता है।
एक ग्राफ का व्यास
सभी चक्करों से अधिकतम विलक्षणता ग्राफ जी के व्यास के रूप में मानी जाती है। एक शीर्ष से सभी अन्य चक्करों के बीच की दूरी को ग्राफ जी के व्यास के रूप में माना जाता है।
Notation − d(G) - एक ग्राफ में कोने की सभी विलक्षणताओं से, जुड़े हुए ग्राफ का व्यास उन सभी विलक्षणताओं की अधिकतम है।
Example
उपरोक्त ग्राफ में, d (G) = 3; जो अधिकतम विलक्षणता है।
केन्द्र बिन्दु
यदि किसी ग्राफ की विलक्षणता उसकी त्रिज्या के बराबर है, तो इसे ग्राफ के केंद्रीय बिंदु के रूप में जाना जाता है। अगर
ई (वी) = आर (वी),
तब 'V' ग्राफ 'G' का केंद्रीय बिंदु है।
Example
उदाहरण ग्राफ में, 'd' ग्राफ का केंद्रीय बिंदु है।
e (d) = r (d) = 2
केन्द्र
'G' के सभी केंद्रीय बिंदुओं के सेट को ग्राफ का केंद्र कहा जाता है।
Example
उदाहरण ग्राफ में, {'d'} ग्राफ का केंद्र है।
परिधि
number of edges in the longest cycle of ‘G’ 'जी' की परिधि के रूप में कहा जाता है।
Example
उदाहरण के ग्राफ में, परिधि 6 है, जिसे हम सबसे लंबे चक्र अकफबेबा या अकफडेबा से प्राप्त करते हैं।
परिधि
'G' के सबसे छोटे चक्र में किनारों की संख्या को इसका गर्थ कहा जाता है।
Notation: जी (G)।
Example - उदाहरण के ग्राफ में, ग्राफ का ग्रन्थ 4 है, जिसे हम सबसे छोटे चक्र एसफैडा या डीएफजी या एबेडा से प्राप्त करते हैं।
ऊर्ध्वाधर प्रमेय की डिग्री का योग
यदि G = (V, E) लंबवत V = {V 1 , V 2 ,… V n } के साथ एक गैर-निर्देशित ग्राफ हो
Corollary 1
यदि G = (V, E) लंबवत V = {V 1 , V 2 ,… V n } के साथ एक निर्देशित ग्राफ हो , तो
Corollary 2
किसी भी गैर-निर्देशित ग्राफ़ में, ऑड डिग्री के साथ कोने की संख्या सम है।
Corollary 3
एक गैर-निर्देशित ग्राफ में, यदि प्रत्येक शीर्ष की डिग्री k है, तो
Corollary 4
गैर-निर्देशित ग्राफ में, यदि प्रत्येक शीर्ष की डिग्री कम से कम k है, तो
| Corollary 5
गैर-निर्देशित ग्राफ में, यदि प्रत्येक शीर्ष की डिग्री अधिकतम k पर है, तो
वर्टिकल की संख्या, किनारों की संख्या, इंटरकनेक्टिविटी और उनकी समग्र संरचना के आधार पर विभिन्न प्रकार के ग्राफ़ होते हैं। हम इस अध्याय में केवल कुछ महत्वपूर्ण प्रकार के रेखांकन पर चर्चा करेंगे।
नल का ग्राफ
A graph having no edges को Null Graph कहा जाता है।
उदाहरण

उपर्युक्त ग्राफ में, 'ए', 'बी' और 'सी' नाम के तीन वर्टीकल हैं, लेकिन उनमें कोई किनारा नहीं है। इसलिए यह एक नल ग्राफ है।
तुच्छ ग्राफ़
ए graph with only one vertex एक तुच्छ ग्राफ कहा जाता है।
उदाहरण

ऊपर दिखाए गए ग्राफ़ में, केवल एक शीर्ष 'a' है जिसमें कोई अन्य किनारा नहीं है। इसलिए यह एक तुच्छ ग्राफ है।
गैर-निर्देशित ग्राफ़
एक गैर-निर्देशित ग्राफ में किनारों होते हैं लेकिन किनारों को निर्देशित नहीं किया जाता है।
उदाहरण
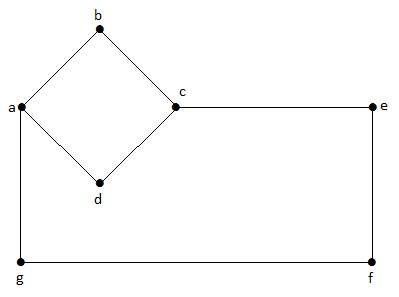
इस ग्राफ में, 'a', 'b', 'c', 'd', 'e', 'f', 'g' वर्टिकल हैं, और 'ab', 'bc', 'cd', 'da ',' एजी ',' जीएफ ',' एफई 'ग्राफ के किनारे हैं। चूंकि यह एक गैर-निर्देशित ग्राफ है, इसलिए किनारों 'अब' और 'बा' समान हैं। इसी तरह अन्य किनारों को भी उसी तरह से माना जाता है।
निर्देशित आलेख
एक निर्देशित ग्राफ में, प्रत्येक किनारे की एक दिशा होती है।
उदाहरण

उपरोक्त ग्राफ में, हमारे पास सात कोने 'ए', 'बी', 'सी', 'डी', 'ई', 'एफ' और 'जी' और 'एब्स', 'सीबी', '' हैं। dc ',' ad ',' ec ',' fe ',' gf ', और' ga '। जैसा कि यह एक निर्देशित ग्राफ है, प्रत्येक किनारे पर एक तीर का निशान होता है जो इसकी दिशा दिखाता है। ध्यान दें कि एक निर्देशित ग्राफ में, 'ab' 'ba' से अलग है।
सरल ग्राफ
एक ग्राफ with no loops और नहीं parallel edges एक सरल ग्राफ कहा जाता है।
'N' वर्टिकल के साथ सिंगल ग्राफ में संभव किनारों की अधिकतम संख्या n C 2 है जहाँ n C 2 = n (n - 1/2) है।
'N' कोने = 2 n c 2 = 2 n (n-1) / 2 के साथ संभव सरल रेखांकन की संख्या ।
उदाहरण
निम्नलिखित ग्राफ में, 3 किनारों के साथ 3 कोने हैं जो समानांतर किनारों और छोरों को छोड़कर अधिकतम है। यह उपरोक्त सूत्रों का उपयोग करके साबित किया जा सकता है।
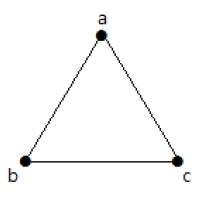
N = 3 कोने वाले किनारों की अधिकतम संख्या -
एन = 3 कोने के साथ सरल रेखांकन की अधिकतम संख्या -
ये 8 रेखांकन नीचे दिखाए गए हैं -
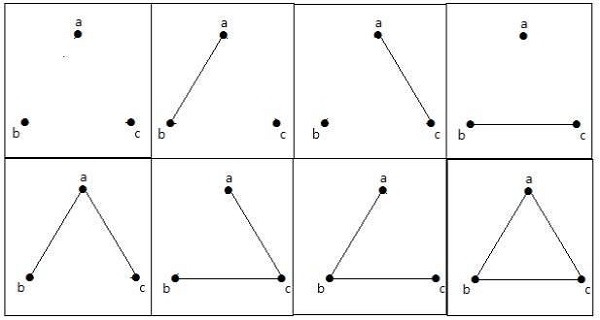
जुड़ा हुआ ग्राफ
एक ग्राफ G को जुड़ा हुआ कहा जाता है if there exists a path between every pair of vertices। ग्राफ में प्रत्येक शीर्ष के लिए कम से कम एक किनारे होना चाहिए। ताकि हम यह कह सकें कि यह किनारे के दूसरी तरफ किसी अन्य शीर्ष से जुड़ा हुआ है।
उदाहरण
निम्नलिखित ग्राफ में, प्रत्येक शीर्ष की अपनी बढ़त दूसरे किनारे से जुड़ी होती है। इसलिए यह एक जुड़ा हुआ ग्राफ है।

डिस्कनेक्ट किया गया ग्राफ़
एक ग्राफ जी काट दिया जाता है, अगर इसमें कम से कम दो जुड़े हुए कोने नहीं होते हैं।
उदाहरण 1
निम्नलिखित ग्राफ एक डिस्कनेक्ट किए गए ग्राफ़ का एक उदाहरण है, जहाँ दो घटक होते हैं, जिनमें से एक '' ए ',' बी ',' सी ',' डी 'वर्टिकल और दूसरा' ई ',' एफ ',' जी 'के साथ होता है। 'ज' वर्टिस।
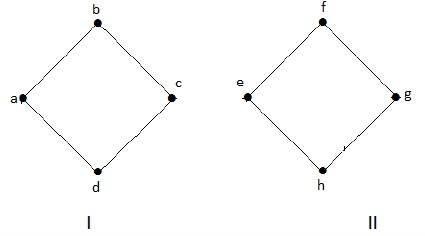
दो घटक स्वतंत्र हैं और एक दूसरे से जुड़े नहीं हैं। इसलिए इसे डिस्कनेक्टेड ग्राफ कहा जाता है।
उदाहरण 2

इस उदाहरण में, दो स्वतंत्र घटक हैं, एब्फ़ और सीडी, जो एक दूसरे से जुड़े नहीं हैं। इसलिए यह एक डिस्कनेक्ट ग्राफ है।
नियमित ग्राफ
एक ग्राफ G को नियमित रूप से कहा जाता है, if all its vertices have the same degree। एक ग्राफ में, यदि प्रत्येक शीर्ष की डिग्री 'के' है, तो ग्राफ को 'के-रेगुलर ग्राफ' कहा जाता है।
उदाहरण
निम्नलिखित रेखांकन में, सभी कोने एक ही डिग्री के हैं। अतः इन रेखांकन को नियमित रेखांकन कहते हैं।
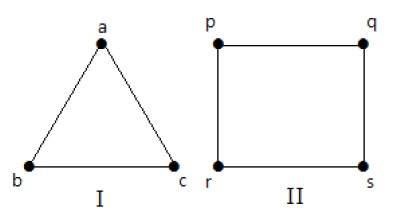
दोनों रेखांकन में, सभी लंबों की डिग्री 2 है। उन्हें 2-नियमित रेखांकन कहा जाता है।
पूरा ग्राफ
'एन' आपसी वर्टिकल वाले सरल ग्राफ को पूर्ण ग्राफ कहा जाता है और यह है denoted by ‘Kn’। ग्राफ में,a vertex should have edges with all other vertices, तो यह एक पूरा ग्राफ कहा जाता है।
दूसरे शब्दों में, यदि एक ग्राफ में एक शीर्ष सभी अन्य कोने से जुड़ा हुआ है, तो इसे पूर्ण ग्राफ़ कहा जाता है।
उदाहरण
निम्नलिखित ग्राफ़ में, ग्राफ़ के प्रत्येक शीर्ष को ग्राफ में शेष सभी शीर्षकों के साथ जोड़ा जाता है, केवल स्वयं को छोड़कर।
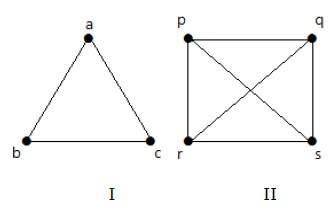
ग्राफ I में,
| ए | ख | सी | |
|---|---|---|---|
| ए | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए |
| ख | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए |
| सी | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं |
ग्राफ II में,
| पी | क्यू | आर | रों | |
|---|---|---|---|---|
| पी | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए | जुड़े हुए |
| क्यू | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए |
| आर | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए |
| रों | जुड़े हुए | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं |
साइकिल का ग्राफ
'N' कोने (n> = 3) और 'n' किनारों वाले एक सरल ग्राफ को एक चक्र ग्राफ कहा जाता है यदि इसके सभी किनारों पर लंबाई 'n' का चक्र होता है।
यदि ग्राफ़ में प्रत्येक शीर्ष की डिग्री दो है, तो इसे एक चक्र ग्राफ़ कहा जाता है।
Notation- सी एन
उदाहरण
निम्नलिखित रेखांकन पर एक नज़र डालें -
ग्राफ I में 3 किनारों के साथ 3 कोने हैं जो एक चक्र 'ab-bc-ca' बना रहा है।
ग्राफ II में 4 किनारों के साथ 4 कोने हैं जो एक चक्र 'pq-qs-sr-rp' बना रहा है।
ग्राफ III में 5 किनारों के साथ 5 कोने हैं जो एक चक्र 'ik-km-ml-lj-ji' का निर्माण कर रहा है।

इसलिए सभी दिए गए रेखांकन चक्र रेखांकन हैं।
व्हील ग्राफ
एक चक्र ग्राफ C n-1 से एक नया वर्सेट जोड़कर प्राप्त किया जाता है । उस नए शीर्ष को कहा जाता है aHubजो C n के सभी कोने से जुड़ा हुआ है ।
संकेतन - डब्ल्यू एन
W n में किनारों की संख्या = हब से किनारों के अन्य सभी कोने तक +
हब के बिना साइकिल ग्राफ में अन्य सभी नोड्स से किनारों की संख्या।
= (n-1) + (n-1)
= 2 (एन -1)
उदाहरण
निम्नलिखित रेखांकन पर एक नज़र डालें। वे सभी व्हील ग्राफ हैं।
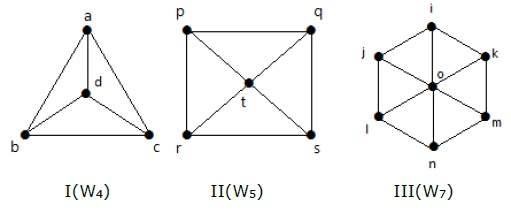
ग्राफ I में, इसे C 3 से 'd' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है । इसे W 4 के रूप में दर्शाया गया है ।
W4 = 2 (n-1) = 2 (3) = 6 में किनारों की संख्या
ग्राफ II में, इसे C4 से 't' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है। इसे W 5 के रूप में दर्शाया गया है ।
W5 = 2 (n-1) = 2 (4) = 8 में किनारों की संख्या
ग्राफ III में, इसे C 6 से 'ओ' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है । इसे W 7 के रूप में दर्शाया गया है ।
W4 = 2 (n-1) = 2 (6) = 12 में किनारों की संख्या
चक्रीय ग्राफ
एक ग्राफ with at least one चक्र को चक्रीय ग्राफ कहा जाता है।
उदाहरण
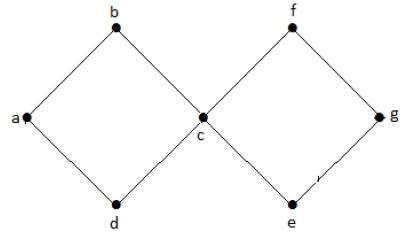
उपर्युक्त उदाहरण के ग्राफ में, हमारे पास दो चक्र हैं abcda और cfgec। इसलिए इसे चक्रीय ग्राफ कहा जाता है।
चक्रीय ग्राफ
एक ग्राफ with no cycles एक चक्रीय ग्राफ कहलाता है।
उदाहरण
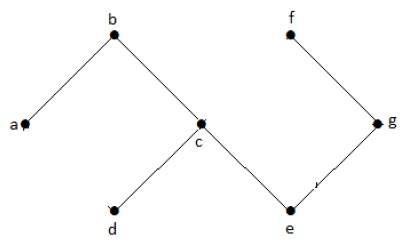
उपरोक्त उदाहरण के ग्राफ में, हमारे पास कोई चक्र नहीं है। इसलिए यह एक गैर-चक्रीय ग्राफ है।
द्विदलीय आलेख
एक साधारण ग्राफ G = (V, E) शीर्ष विभाजन के साथ V = {V 1 , V 2 } को द्विदलीय ग्राफ कहा जाता हैif every edge of E joins a vertex in V1 to a vertex in V2।
सामान्य तौर पर, एक Bipertite ग्राफ में दो सेट होते हैं, आइए हम कहते हैं, V1 और V2, और यदि एक किनारा खींचा जाता है, तो इसे सेट V 2 में किसी भी शीर्ष से किसी भी शीर्ष पर सेट V 2 में किसी भी शीर्ष से कनेक्ट करना चाहिए ।
उदाहरण
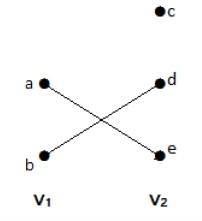
इस ग्राफ में, आप दो सेटों का अवलोकन कर सकते हैं - V 1 और V 2 । यहाँ, 'ae' और 'bd' नाम के दो किनारे दो सेट V 1 और V 2 के वर्टिकल को जोड़ रहे हैं ।
बिपर्टाइट ग्राफ को पूरा करें
एक द्विपक्षीय ग्राफ 'जी', जी = (वी, ई) विभाजन वी के साथ = {वी 1 , वी 2 } अगर वी में हर शिखर एक द्विपक्षीय ग्राफ की पूरी होना कहा जाता है 1 वी के हर शिखर से जुड़ा है 2 ।
सामान्य तौर पर, एक पूरा द्विदलीय ग्राफ सेट वी 2 से प्रत्येक वर्टेक्स को सेट वी 2 से प्रत्येक वर्टेक्स से जोड़ता है ।
उदाहरण
क्योंकि यह सेट वी से प्रत्येक शिखर जोड़ने किनारों है निम्नलिखित ग्राफ एक द्विपक्षीय ग्राफ की पूरी है 1 सेट वी से प्रत्येक शीर्ष करने के लिए 2 ।
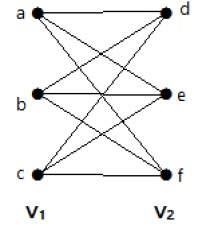
अगर - वी १ | = एम और | वी 2 | = n, तो पूरा bipartite ग्राफ K m, n द्वारा निरूपित किया जाता है ।
- K m, n में (m + n) कोने और (mn) किनारे हैं।
- K m, n एक नियमित ग्राफ है यदि m = n।
सामान्य तौर पर, ए complete bipartite graph is not a complete graph।
K m, n एक पूर्ण ग्राफ है यदि m = n = 1।
एन कोने के साथ एक द्विदलीय ग्राफ में किनारों की अधिकतम संख्या है -
[एन २ / ४]
यदि n = 10, K5, 5 = [n2 / 4] = [10 2 /4] = 25।
इसी प्रकार, K6, 4 = 24
के 7, 3 = 21
के 8, 2 = 16
के 9, 1 = 9
यदि n = 9, k5, 4 = [n2 / 4] = [92/4] = 20
इसी प्रकार, K6, 3 = 18
के 7, 2 = 14
के 8, 1 = 8
यदि 'G' में विषम लंबाई का कोई चक्र नहीं है तो 'G' एक द्विदलीय ग्राफ है। द्विदलीय ग्राफ का एक विशेष मामला एक स्टार ग्राफ है।
स्टार ग्राफ
प्रपत्र K1, n-1 का एक पूर्ण द्विपद ग्राफ n-vertices के साथ एक स्टार ग्राफ है। एक स्टार ग्राफ एक पूर्ण द्विपदीय ग्राफ है यदि एक एकल शीर्ष एक सेट से संबंधित है और सभी शेष कोने दूसरे सेट से संबंधित हैं।
उदाहरण
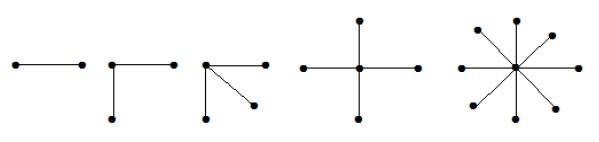
उपर्युक्त रेखांकन में, 'एन' वर्टिकल से बाहर, सभी 'एन -1' वर्टिकल एक ही शीर्ष से जुड़े होते हैं। इसलिए यह K 1 , n-1 के रूप में है जो स्टार ग्राफ हैं।
एक ग्राफ का पूरक
'Gices' को '' G '' के रूप में कुछ छोरों के साथ एक सरल ग्राफ होने दें और एक बढ़त {U, V} 'G present' में मौजूद है, यदि धार G. में मौजूद नहीं है, तो इसका मतलब है, दो कोने समीप हैं 'G ad' में यदि दो कोने G में समीप नहीं हैं।
यदि ग्राफ़ में मौजूद किनारों को दूसरे ग्राफ़ II में अनुपस्थित किया गया है, और यदि ग्राफ़ I और ग्राफ़ II दोनों को एक साथ जोड़कर एक पूर्ण ग्राफ़ बनाया जाता है, तो ग्राफ़ I और ग्राफ़ II को एक दूसरे के पूरक कहा जाता है।
उदाहरण
निम्नलिखित उदाहरण में, ग्राफ- I में दो किनारों 'सीडी' और 'बीडी' हैं। इसके पूरक ग्राफ- II में चार किनारे हैं।
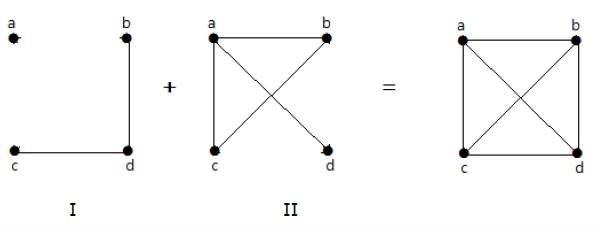
ध्यान दें कि ग्राफ- I में किनारों ग्राफ- II में मौजूद नहीं हैं और इसके विपरीत। इसलिए, दोनों ग्राफों का संयोजन 'एन' वर्टिकल का पूरा ग्राफ देता है।
Note - दो पूरक रेखांकन का एक पूरा ग्राफ देता है।
यदि If जी ’कोई सरल ग्राफ है, तो
| ई (G) | + | ई ('जी -') | = | E (Kn) |, जहाँ n = ग्राफ़ में संख्याओं की संख्या।
उदाहरण
'' जी '' एक सरल ग्राफ है जिसमें नौ कोने और बारह किनारे हैं, 'G-' में किनारों की संख्या ज्ञात करें।
आपके पास है।, E (G) | + | ई ('जी -') | = | ई (एनएन) |
12 + | ई ('जी -') | =
9 (9-1) / 2 = 9 सी 2
12 + | ई ('जी -') | = 36
| ई ( 'जी -') | = 24
'G' 40 किनारों वाला एक सरल ग्राफ है और इसके पूरक 'G has' में 38 किनारे हैं। ग्राफ G या 'G।' में लंबों की संख्या ज्ञात कीजिए।
बता दें कि ग्राफ में वर्टिकल की संख्या 'n' है।
हमारे पास, | ई (जी) | + | ई ('जी -') | = | ई (एनएन) |
40 + 38 = एन (एन -1) / 2
156 = एन (एन -1)
13 (12) = एन (एन -1)
n = 13
पेड़ ऐसे ग्राफ होते हैं जिनमें एक भी चक्र नहीं होता है। वे चित्रमय रूप में पदानुक्रमित संरचना का प्रतिनिधित्व करते हैं। पेड़ ग्राफ के सबसे सरल वर्ग के हैं। उनकी सादगी के बावजूद, उनके पास एक समृद्ध संरचना है।
पेड़ कंप्यूटर विज्ञान की डेटा संरचनाओं में पेड़ के रूप में जटिल के रूप में सरल रूप में उपयोगी अनुप्रयोगों की एक श्रृंखला प्रदान करते हैं।
पेड़
ए connected acyclic graphपेड़ कहलाता है। दूसरे शब्दों में, बिना किसी चक्र के जुड़े हुए ग्राफ को वृक्ष कहा जाता है।
एक पेड़ के किनारों के रूप में जाना जाता है branches। पेड़ों के तत्वों को उनके नोड्स कहा जाता है। बिना बाल नोड्स के नोड्स को कहा जाता हैleaf nodes।
'एन' वर्टीकल वाले पेड़ में 'एन -1' किनारे होते हैं। यदि इसमें 'n-1' की तुलना में एक और किनारे अतिरिक्त है, तो अतिरिक्त किनारे को स्पष्ट रूप से दो कोने के साथ जोड़ना होगा, जिससे एक चक्र बनता है। फिर, यह एक चक्रीय ग्राफ बन जाता है जो पेड़ के ग्राफ का उल्लंघन है।
Example 1
यहां दिखाया गया ग्राफ एक पेड़ है क्योंकि इसमें कोई चक्र नहीं है और यह जुड़ा हुआ है। परिभाषा में उल्लिखित 'एन' कोने 'एन -1' किनारों के लिए इसके चार कोने और तीन किनारे हैं।
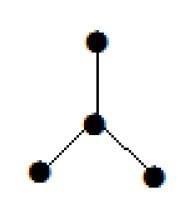
Note - हर पेड़ में डिग्री एक के कम से कम दो कोने होते हैं।
Example 2
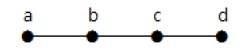
उपरोक्त उदाहरण में, शीर्षकों 'a' और 'd' में डिग्री एक है। और अन्य दो कोने 'बी' और 'सी' की डिग्री दो हैं। यह संभव है क्योंकि चक्र नहीं बनाने के लिए, ग्राफ़ में कहीं भी कम से कम दो एकल किनारे होने चाहिए। यह एक डिग्री के साथ दो किनारों के अलावा कुछ भी नहीं है।
वन
ए disconnected acyclic graphजंगल कहलाता है। दूसरे शब्दों में, पेड़ों के एक निराशाजनक संग्रह को जंगल कहा जाता है।
Example
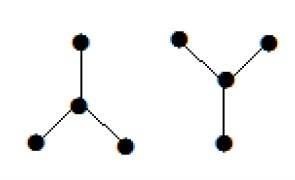
निम्न ग्राफ़ दो उप-ग्राफ़ की तरह दिखता है; लेकिन यह एक एकल डिस्कनेक्ट ग्राफ है। इस ग्राफ में कोई चक्र नहीं हैं। इसलिए, स्पष्ट रूप से यह एक जंगल है।
फैलते हुए पेड़
मान लीजिए कि G एक जुड़ा हुआ ग्राफ़ है, तो G के उप-ग्राफ़ को G का एक फैले हुए वृक्ष कहा जाता है -
- एच एक पेड़ है
- H में G के सभी कोने हैं।
अप्रत्यक्ष ग्राफ G का एक फैले हुए पेड़ T एक सबग्राफ है जिसमें G के सभी कोने शामिल हैं।
Example

उपरोक्त उदाहरण में, G एक जुड़ा हुआ ग्राफ है और H, G का उप-ग्राफ है।
स्पष्ट रूप से, ग्राफ एच में कोई चक्र नहीं है, यह छह किनारों वाला एक पेड़ है जो कुल संख्याओं की तुलना में कम है। इसलिए H, G का स्पानिंग ट्री है।
सर्किट रैंक
Let G ’को 'n’ कोने और edges m ’किनारों से जुड़ा ग्राफ होने दें। जी के एक फैले हुए वृक्ष 'T' में (n-1) किनारे होते हैं।
इसलिए, एक फैले हुए पेड़ = m- (n-1) को प्राप्त करने के लिए आपको किनारों की संख्या को 'G' से हटाना होगा, जिसे G की सर्किट रैंक कहा जाता है।
यह सूत्र सत्य है, क्योंकि एक फैले हुए वृक्ष में आपको 'एन -1' किनारों की आवश्यकता होती है। 'M' किनारों में से, आपको ग्राफ़ में 'n-1' किनारों को रखने की आवश्यकता है।
इसलिए, 'मी' से 'एन -1' किनारों को हटाने से किनारों को ग्राफ से हटा दिया जाता है ताकि एक फैले हुए पेड़ को प्राप्त किया जा सके, जिसे एक चक्र नहीं बनाना चाहिए।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
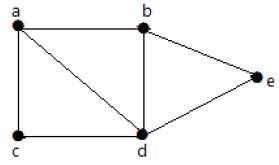
उपरोक्त उदाहरण में दिए गए ग्राफ के लिए, आपके पास m = 7 किनारे और n = 5 कोने हैं।
फिर सर्किट रैंक है -
Example
बता दें कि 'G' छह वर्टिकल के साथ एक जुड़ा हुआ ग्राफ है और प्रत्येक शीर्ष की डिग्री तीन है। 'G' का सर्किट रैंक ज्ञात कीजिए।
कार्यक्षेत्र प्रमेय की डिग्री के योग से,
किरचॉफ की प्रमेय
किरचॉफ का प्रमेय एक फैले हुए ग्राफ से बनने वाले पेड़ों की संख्या का पता लगाने में उपयोगी है।
Example
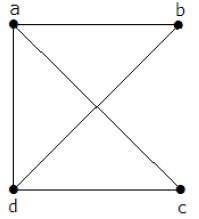
मैट्रिक्स 'ए' को भरा जाना चाहिए, यदि दो कोने के बीच एक धार है, तो इसे '1' के रूप में दिया जाना चाहिए, अन्यथा '0'।
$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$किर्चॉफ के प्रमेय का उपयोग करके, इसे तिरछे और अन्य सभी तत्वों की डिग्री के साथ सिद्धांत विकर्ण मूल्यों की जगह के रूप में बदला जाना चाहिए।
$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$इस प्रकार, फैले पेड़ों की संख्या = 8।
क्या किसी ग्राफ को एक शीर्ष से दूसरे तक ले जाना संभव है, यह निर्धारित किया जाता है कि ग्राफ़ कैसे जुड़ा है। ग्राफ थ्योरी में कनेक्टिविटी एक मूल अवधारणा है। कनेक्टिविटी परिभाषित करती है कि क्या एक ग्राफ जुड़ा हुआ है या डिस्कनेक्ट किया गया है। इसमें किनारे और वर्टेक्स के आधार पर सबटॉपिक्स हैं, जिन्हें एज कनेक्टिविटी और वर्टेक्स कनेक्टिविटी के रूप में जाना जाता है। आइए हम उनके बारे में विस्तार से चर्चा करें।
कनेक्टिविटी
एक ग्राफ कहा जाता है connected if there is a path between every pair of vertex। प्रत्येक शीर्ष से किसी भी अन्य शीर्ष पर, कुछ मार्ग को पार करने के लिए होना चाहिए। इसे एक ग्राफ की कनेक्टिविटी कहा जाता है। कई डिस्कनेक्ट किए गए कोने और किनारों के साथ एक ग्राफ को डिस्कनेक्ट करने के लिए कहा जाता है।
Example 1
निम्नलिखित ग्राफ में, एक शीर्ष से किसी अन्य शीर्ष पर यात्रा करना संभव है। उदाहरण के लिए, व्यक्ति 'ab-e' पथ का उपयोग करके 'a' से 'vertex' तक पहुँच सकता है।
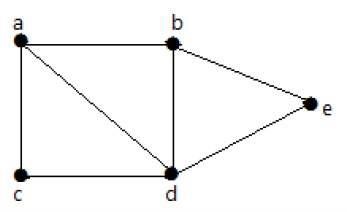
Example 2
निम्नलिखित उदाहरण में, शीर्ष 'क' से 'वर्टेक्स' च 'तक ट्रेस करना संभव नहीं है क्योंकि उनके बीच प्रत्यक्ष या अप्रत्यक्ष रूप से कोई रास्ता नहीं है। इसलिए यह एक डिस्कनेक्ट ग्राफ है।
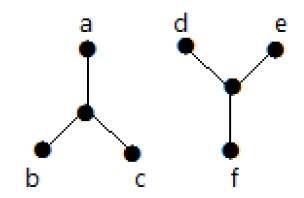
कट वर्टेक्स
'G' को एक कनेक्टेड ग्राफ होने दें। एक वर्टेक्स V is G को 'G' का कट वर्टेक्स कहा जाता है, यदि 'G-V' ('G' से 'V' हटाएं) के परिणाम डिस्कनेक्ट हो जाते हैं। एक ग्राफ से कटा हुआ शीर्ष हटाने से इसे दो या दो से अधिक ग्राफ़ में तोड़ दिया जाता है।
Note - कटी हुई चोटी को हटाने से एक ग्राफ काट दिया जा सकता है।
कनेक्टेड ग्राफ 'G' में अधिकतम (n-2) कटे हुए कोने हो सकते हैं।
Example
निम्नलिखित ग्राफ में, 'ई' और 'सी' कटे हुए कोने हैं।

Will e ’या 'c’ को हटाने से ग्राफ डिसकनेक्टेड ग्राफ बन जाएगा।

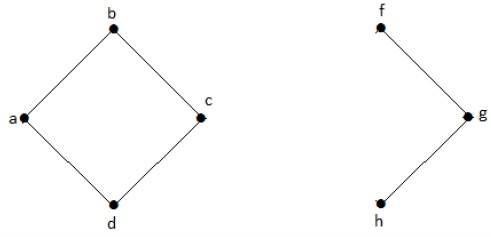
Without जी ’के बिना, वर्टेक्स and सी’ और वर्टेक्स and एच ’और कई अन्य के बीच कोई रास्ता नहीं है। इसलिए यह कट ईट के साथ 'ई' के रूप में डिस्कनेक्ट किया गया ग्राफ़ है। इसी प्रकार, 'ग' भी उपरोक्त ग्राफ के लिए एक कटा हुआ शीर्ष है।
कट एज (पुल)
'G' को एक कनेक्टेड ग्राफ होने दें। यदि 'G-e' डिस्कनेक्ट किए गए ग्राफ़ में परिणामित होता है, तो एक धार 'e' is G को कट एज कहा जाता है।
यदि किसी ग्राफ़ में किसी किनारे को हटाने से दो या दो से अधिक ग्राफ़ निकलते हैं, तो उस किनारे को कट एज कहा जाता है।
Example
निम्नलिखित ग्राफ में, कट किनारे [(सी, ई)] है।

ग्राफ से किनारे (सी, ई) को हटाकर, यह डिस्कनेक्ट किया गया ग्राफ बन जाता है।


उपरोक्त ग्राफ़ में, किनारे (सी, ई) को हटाने से ग्राफ़ दो में टूट जाता है जो डिस्कनेक्ट किए गए ग्राफ़ के अलावा कुछ भी नहीं है। इसलिए, बढ़त (c, e) ग्राफ का एक कटा हुआ किनारा है।
Note - 'G' को 'n' वर्टिक्स के साथ जुड़ा हुआ ग्राफ माना जाता है
एक कट एज ई if जी अगर और केवल अगर धार 'ई' जी में किसी भी चक्र का हिस्सा नहीं है।
कटे हुए किनारों की अधिकतम संख्या संभव है 'एन -1'।
जब भी कटे हुए किनारे मौजूद होते हैं, तो कटे हुए कोने भी मौजूद होते हैं क्योंकि कटे हुए किनारे का कम से कम एक शीर्ष कटे हुए शीर्ष वाला होता है।
यदि एक कट वर्टेक्स मौजूद है, तो एक कट एज मौजूद हो सकता है या नहीं।
एक ग्राफ का कट सेट
'G' = (V, E) को एक जुड़ा हुआ ग्राफ होने दें। E के एक उपसमूह E को G का कट सेट कहा जाता है यदि G से E के सभी किनारों को हटा दिया जाए तो G डिस्कनेक्ट हो जाता है।
यदि ग्राफ़ से कुछ निश्चित किनारों को हटाने से यह डिस्कनेक्ट हो जाता है, तो उन हटाए गए किनारों को ग्राफ़ का कट सेट कहा जाता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें। इसका कट सेट E1 = {e1, e3, e5, e8} है।
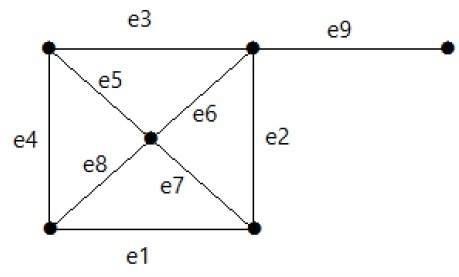
ग्राफ से कट सेट E1 को हटाने के बाद, यह निम्नानुसार दिखाई देगा -
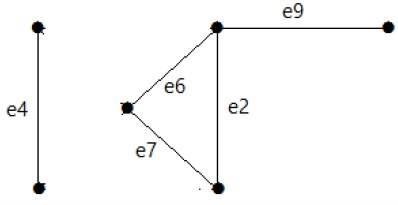
इसी तरह, अन्य कट सेट हैं जो ग्राफ़ को डिस्कनेक्ट कर सकते हैं -
E3 = {e9} - ग्राफ़ का सबसे छोटा कट सेट।
E4 = {e3, e4, e5}
एज कनेक्टिविटी
'G' को एक कनेक्टेड ग्राफ होने दें। किनारों की न्यूनतम संख्या जिसका निष्कासन 'G' काटता है, को G की किनारे कनेक्टिविटी कहा जाता है।
Notation - Iλ (G)
दूसरे शब्दों में, number of edges in a smallest cut set of G को G की एज कनेक्टिविटी कहा जाता है।
यदि 'G' में एक कट एज है, तो λ (G) 1. है (G. की बढ़त कनेक्टिविटी)
Example
निम्नलिखित ग्राफ पर एक नज़र डालें। दो न्यूनतम किनारों को हटाने से, जुड़ा हुआ ग्राफ डिस्कनेक्ट हो जाता है। इसलिए, इसका एज कनेक्टिविटी (λ (G)) 2 है।
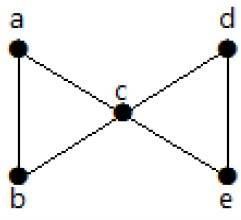
यहां दो किनारों को हटाकर ग्राफ को डिस्कनेक्ट करने के चार तरीके दिए गए हैं -

वर्टेक्स कनेक्टिविटी
'G' को एक कनेक्टेड ग्राफ होने दें। उन लंबों की न्यूनतम संख्या, जिनके निष्कासन से 'G' या तो डिस्कनेक्ट हो जाता है या एक तुच्छ ग्राफ में 'G' को कम कर देता है, इसे वर्टेक्स कनेक्टिविटी कहा जाता है।
Notation - के (जी)
Example
उपरोक्त ग्राफ में, 'ई' और 'आई' को हटाकर ग्राफ को डिस्कनेक्ट कर दिया गया है।

यदि जी में एक कट वर्टेक्स है, तो K (G) = 1।
Notation - किसी भी जुड़े ग्राफ G के लिए,
K (G) λ λ (G) δ ≤ (G)
वर्टेक्स कनेक्टिविटी (K (G)), एज कनेक्टिविटी (λ (G)), G () (G)) की न्यूनतम संख्या।
Example
निम्नलिखित ग्राफ के लिए λ (G) और K (G) की गणना करें -
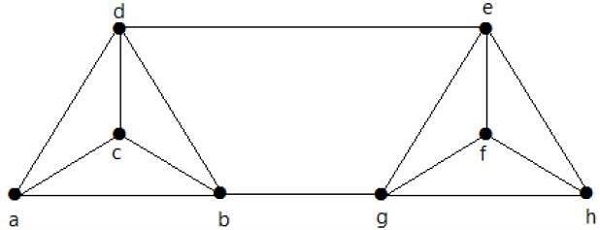
Solution
ग्राफ से,
= (जी) = 3
K (G) (λ (G) δ ≤ (G) = 3 (1)
के (जी) (2 (2)
किनारों को हटाना {d, e} और {b, h}, हम G को डिस्कनेक्ट कर सकते हैं।
इसलिए,
λ (जी) = 2
2 δ λ (G) δ ≤ (G) = 2 (3)
से (2) और (3), वर्टेक्स कनेक्टिविटी K (G) = 2
एक कवरिंग ग्राफ एक सबग्राफ है जिसमें किसी भी अन्य ग्राफ के अनुरूप सभी कोने या सभी किनारे होते हैं। एक सबग्राफ जिसमें सभी कोने होते हैं, a कहलाता हैline/edge covering। एक उपसमूह जिसमें सभी किनारे होते हैं, a कहलाता हैvertex covering।
लाइन कवरिंग
G = (V, E) को एक ग्राफ बनाएं। एक सबसेट C (E) को G की एक रेखा कहा जाता है यदि G के प्रत्येक शीर्ष पर C, यानी C में कम से कम एक किनारे के साथ घटना है
deg (V) ≥ 1 ∈ V V जी
क्योंकि प्रत्येक शीर्ष एक किनारे से दूसरे शीर्ष के साथ जुड़ा हुआ है। इसलिए इसकी न्यूनतम 1 डिग्री है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
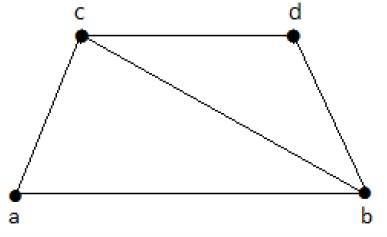
इसके सबग्राफ में लाइन कवरिंग निम्नानुसार हैं -
सी 1 = {{ए, बी}, {सी, डी}}
सी 2 = {{ए, डी}, {बी, सी}}
सी 3 = {{ए, बी}, {बी, सी}, {बी, डी}}
सी 4 = {{ए, बी}, {बी, सी}, {सी, डी}}
'G' की लाइन कवरिंग मौजूद नहीं है अगर और केवल 'G' में एक अलग वर्टेक्स हो। 'N' वर्टिकल के साथ ग्राफ के लाइन कवरिंग में कम से कम [n / 2] किनारे होते हैं।
मिनिमल लाइन कवरिंग
एक ग्राफ G के C को कवर करने वाली रेखा को न्यूनतम कहा जाता है if no edge can be deleted from C।
Example
उपर्युक्त ग्राफ में, लाइन कवरिंग वाले सबग्राफ निम्नानुसार हैं -
सी 1 = {{ए, बी}, {सी, डी}}
सी 2 = {{ए, डी}, {बी, सी}}
सी 3 = {{ए, बी}, {बी, सी}, {बी, डी}}
सी 4 = {{ए, बी}, {बी, सी}, {सी, डी}}
यहां, C 1 , C 2 , C 3 न्यूनतम लाइन कवरिंग हैं, जबकि C 4 इसलिए नहीं है क्योंकि हम {b, c} को हटा सकते हैं।
न्यूनतम लाइन कवरिंग
इसे के रूप में भी जाना जाता है Smallest Minimal Line Covering। न्यूनतम संख्या किनारों के साथ कवर करने वाली एक न्यूनतम रेखा को 'जी' की न्यूनतम रेखा को कवर किया जाता है। 'G' में न्यूनतम रेखा को कवर करने वाले किनारों की संख्या को कहा जाता हैline covering numberof 'G' (α 1 )।
Example
उपरोक्त उदाहरण में, C 1 और C 2 , G और α 1 = 2 की न्यूनतम रेखा है ।
हर लाइन कवरिंग में एक न्यूनतम लाइन कवरिंग होती है।
हर लाइन कवरिंग में न्यूनतम लाइन कवरिंग नहीं होती है (C 3 में कोई न्यूनतम लाइन कवरिंग नहीं होती है।
कोई न्यूनतम पंक्ति कवर में एक चक्र नहीं होता है।
यदि 'C' को कवर करने वाली रेखा में लंबाई 3 या अधिक का कोई पथ नहीं है, तो 'C' एक न्यूनतम रेखा है, क्योंकि 'C' के सभी घटक स्टार ग्राफ हैं और स्टार ग्राफ से, कोई भी किनारे नहीं हटाया जा सकता है।
वर्टेक्स कवरिंग
चलो 'जी' = (वी, ई) एक ग्राफ हो। V के एक उपसमूह K को 'G' का एक शीर्ष आवरण कहा जाता है, यदि 'G' के प्रत्येक किनारे पर 'K' में एक शीर्ष रेखा के साथ घटना या आवरण होता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
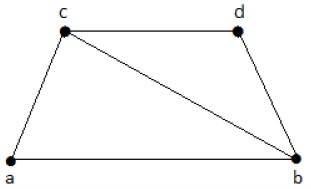
उपर्युक्त ग्राफ़ से प्राप्त किए जा सकने वाले उपसमूह इस प्रकार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}
K 4 = {a, d}
यहाँ, K 1 , K 2 , और K 3 में वर्टेक्स कवरिंग है, जबकि K 4 में कोई वर्टेक्स कवर नहीं है क्योंकि यह एज {bc} को कवर नहीं करता है।
न्यूनतम वर्टेक्स कवरिंग
ग्राफ 'जी' के एक शीर्ष 'के' को न्यूनतम कवर कहा जाता है यदि कोई शीर्ष 'के' से हटाया नहीं जा सकता है।
Example
उपर्युक्त ग्राफ में, शीर्ष कवर करने वाले उपसमूह निम्नानुसार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}
यहाँ, K 1 और K 2 न्यूनतम वर्टिकल कवरिंग हैं, जबकि K 3 में , वर्टेक्स 'd' को हटाया जा सकता है।
न्यूनतम वर्टेक्स कवरिंग
इसे सबसे छोटी न्यूनतम शीर्ष आवरण के रूप में भी जाना जाता है। न्यूनतम संख्या शीर्ष वाले ग्राफ 'G' को कवर करने वाले न्यूनतम शीर्ष को न्यूनतम शीर्ष आवरण कहा जाता है।
'G' के न्यूनतम वर्टिकल कवरिंग में वर्टिस की संख्या को G (α 2 ) की वर्टिकल कवरिंग संख्या कहा जाता है ।
Example
निम्नलिखित ग्राफ में, शीर्ष कवर करने वाले सबग्राफ निम्नानुसार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}

यहां, K 1 , G का एक न्यूनतम शीर्ष कवर है, क्योंकि इसमें केवल दो कोने हैं। α 2 = 2।
मैचिंग ग्राफ एक ग्राफ का एक सबग्राफ होता है जहाँ एक दूसरे से सटे कोई किनारे नहीं होते हैं। बस, किसी भी दो किनारों के बीच कोई सामान्य शीर्ष नहीं होना चाहिए।
मेल मिलाना
चलो 'जी' = (वी, ई) एक ग्राफ हो। सबग्राफ को एक मिलान M (G) कहा जाता है,if each vertex of G is incident with at most one edge in M, अर्थात,
deg (V) ≤ 1 ∈ V V जी
जिसका मतलब है कि मिलान ग्राफ M (G) में, कोने में 1 या 0 की डिग्री होनी चाहिए, जहां किनारों को ग्राफ G पर घटना होना चाहिए।
Notation - एम (जी)
Example
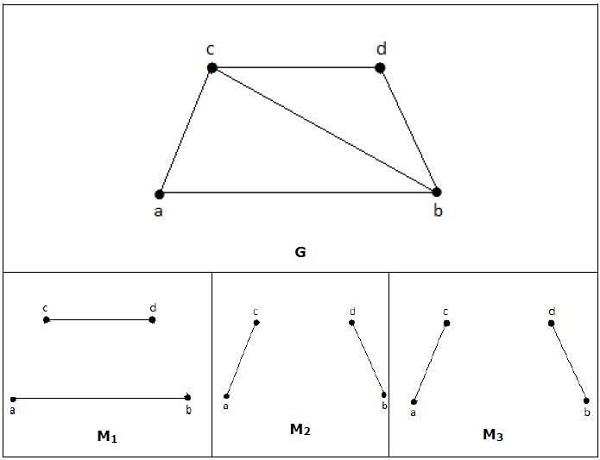

एक मेल में,
if deg(V) = 1, then (V) is said to be matched
if deg(V) = 0, then (V) is not matched.
In a matching, no two edges are adjacent. It is because if any two edges are adjacent, then the degree of the vertex which is joining those two edges will have a degree of 2 which violates the matching rule.
Maximal Matching
A matching M of graph ‘G’ is said to maximal if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 from the above graph are the maximal matching of G.
Maximum Matching
It is also known as largest maximal matching. Maximum matching is defined as the maximal matching with maximum number of edges.
The number of edges in the maximum matching of ‘G’ is called its matching number.
Example
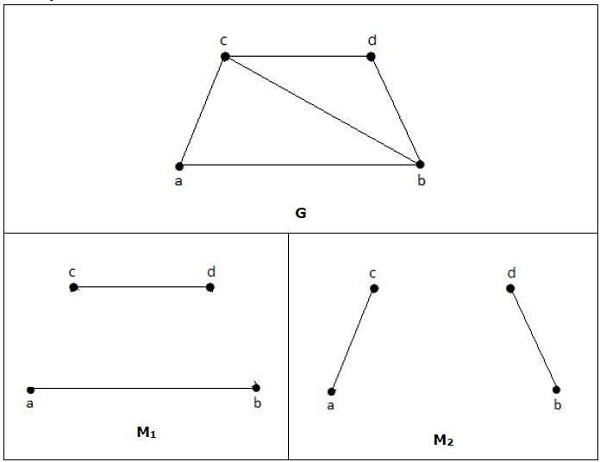
For a graph given in the above example, M1 and M2 are the maximum matching of ‘G’ and its matching number is 2. Hence by using the graph G, we can form only the subgraphs with only 2 edges maximum. Hence we have the matching number as two.
Perfect Matching
A matching (M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e.,
deg(V) = 1 ∀ V
The degree of each and every vertex in the subgraph should have a degree of 1.
Example
In the following graphs, M1 and M2 are examples of perfect matching of G.
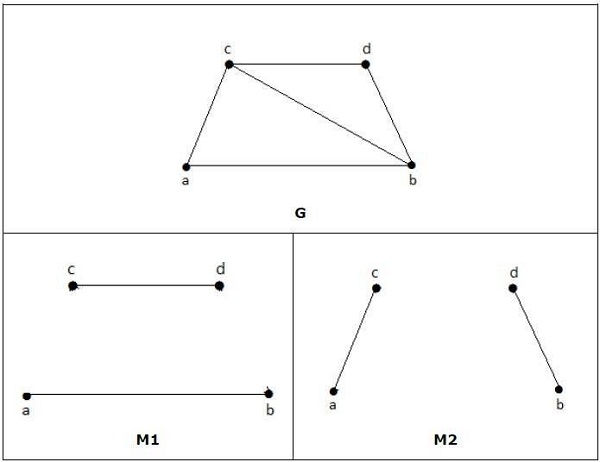
Note − Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.
A maximum matching of graph need not be perfect. If a graph ‘G’ has a perfect match, then the number of vertices |V(G)| is even. If it is odd, then the last vertex pairs with the other vertex, and finally there remains a single vertex which cannot be paired with any other vertex for which the degree is zero. It clearly violates the perfect matching principle.
Example
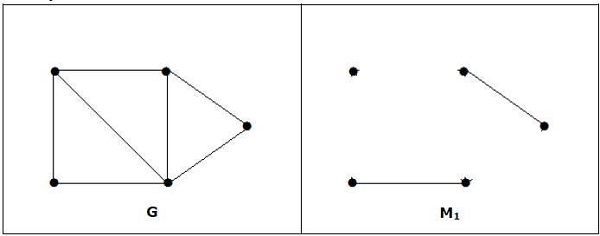
Note − The converse of the above statement need not be true. If G has even number of vertices, then M1 need not be perfect.
Example
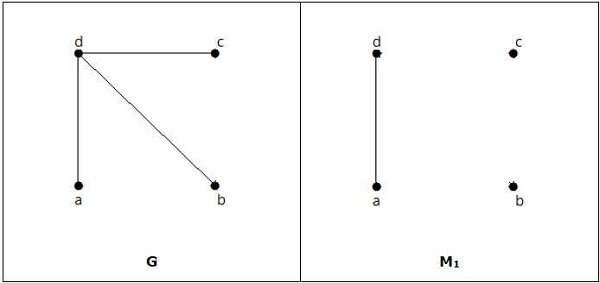
It is matching, but it is not a perfect match, even though it has even number of vertices.
Independent sets are represented in sets, in which
there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.
there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.
Independent Line Set
Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.
Example
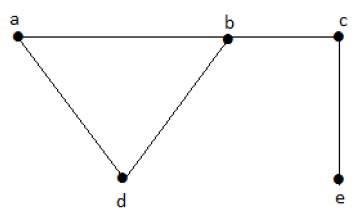
Let us consider the following subsets −
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.
Maximal Independent Line Set
An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.
Example
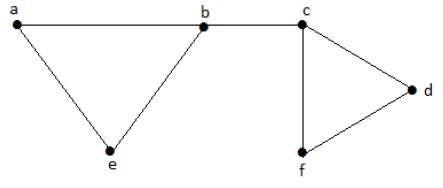
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L2 and L3 are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.
Maximum Independent Line Set
A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
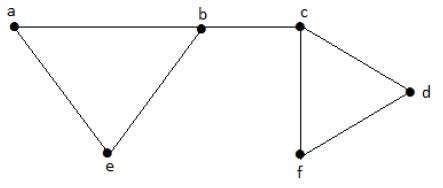
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L3 is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.
Note − For any graph G with no isolated vertex,
α1 + β1 = number of vertices in a graph = |V|
Example
Line covering number of Kn/Cn/wn,
$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$Line independent number (Matching number) = β1 = [n/2] α1 + β1 = n.
Independent Vertex Set
Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.
Example

Consider the following subsets from the above graphs −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Clearly S1 is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S2, S3, and S4 are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.
मैक्सिमल इंडिपेंडेंट वर्टेक्स सेट
बता दें कि 'G' एक ग्राफ है, तो 'G' का एक स्वतंत्र शीर्ष सेट अधिकतम कहा जाता है यदि 'G' के किसी अन्य शीर्ष को 'S' में नहीं जोड़ा जा सकता है।
Example
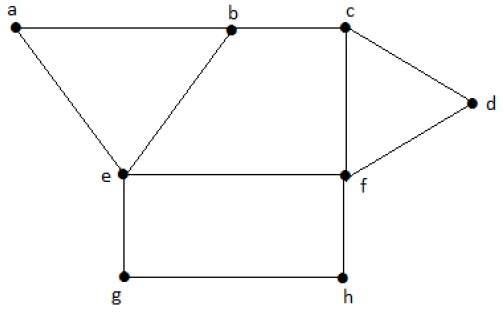
उपरोक्त रेखांकन से निम्नलिखित सबसेट पर विचार करें।
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}एस 2 और एस 3 'जी' के अधिकतम स्वतंत्र शीर्ष सेट हैं। एस 1 और एस 4 में , हम अन्य कोने जोड़ सकते हैं; लेकिन S 2 और S 3 में , हम कोई अन्य शीर्ष जोड़ नहीं सकते।
अधिकतम स्वतंत्र वर्सेट सेट
अधिकतम संख्याओं के साथ 'G' के एक अधिकतम स्वतंत्र शीर्ष सेट को अधिकतम स्वतंत्र शीर्ष सेट कहा जाता है।
Example

उपरोक्त ग्राफ से निम्नलिखित सबसेट पर विचार करें -
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}केवल S 3 अधिकतम स्वतंत्र शीर्ष सेट है, क्योंकि यह वर्टिकल की अधिकतम संख्या को कवर करता है। 'G' के अधिकतम स्वतंत्र शीर्ष सेट में कोने की संख्या को G ( । 2 ) का स्वतंत्र शीर्ष संख्या कहा जाता है ।
Example
पूरा ग्राफ K n के लिए ,
वर्टेक्स कवरिंग संख्या = α 2 = n 1
वर्टेक्स स्वतंत्र संख्या = = 2 = 1
आपके पास α 2 + = 2 = n है
एक पूर्ण ग्राफ में, प्रत्येक शीर्ष उसके शेष (n - 1) कोने के निकट है। इसलिए, K n के अधिकतम स्वतंत्र सेट में केवल एक शीर्ष होता है।
इसलिए, = 2 = 1
और α 2 = | वी | - n 2 = एन -1
Note - किसी भी ग्राफ के लिए 'G' = (V, E)
- α 2 + β 2 = | v |
- यदि 'S' 'G' का एक स्वतंत्र शीर्ष सेट है, तो (V - S) G का एक शीर्ष कवर है।
ग्राफ़ रंग कुछ और नहीं, कुछ बाधाओं के तहत ग्राफ घटकों जैसे कि कोने, किनारों और क्षेत्रों को लेबल करने का एक सरल तरीका है। एक ग्राफ़ में, कोई भी दो आसन्न कोने, आसन्न किनारे, या आसन्न क्षेत्र न्यूनतम संख्या में रंगों के साथ रंगीन नहीं होते हैं। इस संख्या को कहा जाता हैchromatic number और ग्राफ को a कहा जाता है properly colored graph।
ग्राफ़ की रंगाई करते समय, ग्राफ़ पर सेट की गई बाधाएँ रंग, रंग क्रम, रंग निर्दिष्ट करने का तरीका, आदि रंग एक शीर्ष या किसी विशेष क्षेत्र को दिए जाते हैं। इस प्रकार, समान रंग वाले क्षेत्र या क्षेत्र स्वतंत्र सेट बनाते हैं।
वर्टेक्स रंग
वर्टेक्स रंग एक ग्राफ 'जी' के कोने को रंगों का एक असाइनमेंट है, जैसे कि दो आसन्न कोने में एक ही रंग नहीं है। सीधे शब्दों में कहें, एक किनारे के कोई भी दो कोने एक ही रंग के नहीं होने चाहिए।
क्रोमेटिक नंबर
ग्राफ 'जी' के वर्टेक्स रंग के लिए आवश्यक रंगों की न्यूनतम संख्या को एक्स (जी) द्वारा चिह्नित जी के क्रोमेटिक नंबर के रूप में कहा जाता है।
1 (G) = 1 यदि और केवल यदि 'G' एक शून्य ग्राफ है। यदि If G ’शून्य ग्राफ नहीं है, तो G (G) not 2।
Example
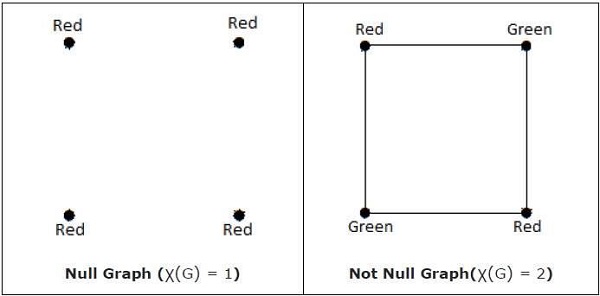
Note - एक ग्राफ 'जी' को एन-कवर करने योग्य कहा जाता है यदि कोई शीर्ष रंग होता है जो कि अधिकांश एन रंगों का उपयोग करता है, अर्थात, एक्स (जी)। एन।
क्षेत्र का रंग
रीजन कलरिंग एक प्लानर ग्राफ के क्षेत्रों के लिए रंगों का एक असाइनमेंट है जैसे कि दो आसन्न क्षेत्रों में एक ही रंग नहीं है। कहा जाता है कि दो क्षेत्रों के पास एक सामान्य किनारा है।
Example
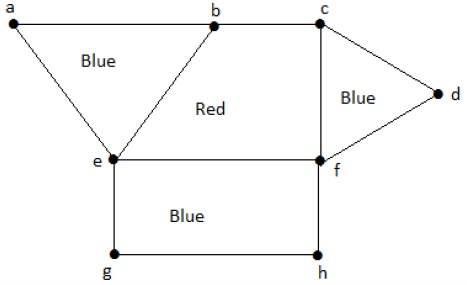
निम्नलिखित ग्राफ पर एक नज़र डालें। क्षेत्र 'एईबी' और 'बीफसी' आसन्न हैं, क्योंकि उन दोनों क्षेत्रों के बीच एक सामान्य बढ़त है।
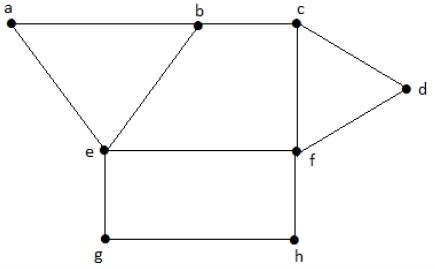
इसी प्रकार, अन्य क्षेत्र भी आसन्न के आधार पर रंगीन होते हैं। यह ग्राफ निम्नानुसार रंगीन है -
Example
Kn की वर्णनात्मक संख्या है
- n
- n–1
- [n/2]
- [n/2]
के 4 के साथ इस उदाहरण पर विचार करें ।

पूर्ण ग्राफ में, प्रत्येक शीर्ष शेष (n - 1) कोने के समीप है। इसलिए, प्रत्येक शीर्ष को एक नए रंग की आवश्यकता होती है। इसलिए K n = n की वर्णक्रमीय संख्या ।
ग्राफ रंगाई के अनुप्रयोग
ग्राफ सिद्धांत, ग्राफ सिद्धांत में सबसे महत्वपूर्ण अवधारणाओं में से एक है। इसका उपयोग कंप्यूटर विज्ञान के कई वास्तविक समय के अनुप्रयोगों में किया जाता है जैसे -
- Clustering
- डेटा माइनिंग
- छवि कैप्चरिंग
- छवि विभाजन
- Networking
- संसाधन आवंटन
- शेड्यूलिंग प्रक्रियाएं
एक ग्राफ विभिन्न रूपों में मौजूद हो सकता है जिसमें एक ही संख्या में कोने, किनारे और एक ही किनारे की कनेक्टिविटी होती है। ऐसे ग्राफ को आइसोमॉर्फिक ग्राफ कहा जाता है। ध्यान दें कि हम इस अध्याय में ग्राफ़ को मुख्य रूप से उन्हें संदर्भित करने और उन्हें एक दूसरे से पहचानने के उद्देश्य से लेबल करते हैं।
आइसोमोर्फिक रेखांकन
दो ग्राफ G 1 और G 2 को आइसोमोर्फिक कहा जाता है यदि -
उनके घटकों की संख्या (कोने और किनारे) समान हैं।
उनकी बढ़त कनेक्टिविटी बरकरार है।
Note- संक्षेप में, दो आइसोमॉर्फिक ग्राफ़ों में से, एक दूसरे का एक संपादित संस्करण है। एक अनलेबल ग्राफ को एक आइसोमॉर्फिक ग्राफ के रूप में भी सोचा जा सकता है।
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
यदि जी 1 G जी 2 तो -
| वी (जी 1 ) | = | वी (जी 2 ) |
| ई (जी 1 ) | = | ई (जी 2 ) |
जी 1 और जी 2 के डिग्री अनुक्रम समान हैं।
यदि कोने {V 1 , V 2 , .. Vk} G 1 में लंबाई K का एक चक्र बनाते हैं , तो कोने {f (V 1 ), f (V 2 ),… f (Vk)} को एक चक्र बनाना चाहिए। जी 2 में लंबाई के ।
उपरोक्त सभी स्थितियाँ ग्राफ 1 और G 2 के लिए आइसोमोर्फिक होना आवश्यक है, लेकिन यह साबित करने के लिए पर्याप्त नहीं है कि ग्राफ आइसोमॉर्फिक हैं।
(G 1 G G 2 ) यदि और केवल अगर (G 1 - - G 2 -) जहां G 1 और G 2 सरल रेखांकन हैं।
(G 1 G G 2 ) यदि G 1 और G 2 के आसन्न मैट्रिक्स समान हैं।
(G 1 G G 2 ) यदि और केवल अगर G 1 और G 2 के संगत उपसमूह (G1 में कुछ कोने हटाकर और ग्राफ G 2 में उनकी छवियां ) आइसोमोर्फिक हैं।
Example
निम्नलिखित में से कौन सा ग्राफ आइसोमॉर्फिक है?
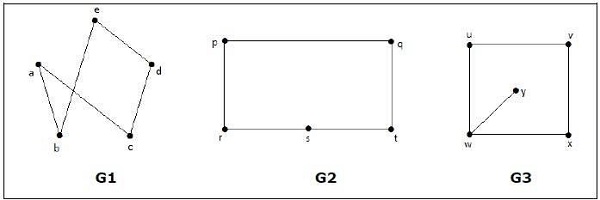
ग्राफ जी 3 में , वर्टेक्स 'डब्ल्यू' में केवल डिग्री 3 होती है, जबकि अन्य सभी ग्राफ वर्टिकल में डिग्री 2 होती है। इसलिए जी 3 आइसोमॉर्फिक से जी 1 या जी 2 नहीं है ।
जी 1 और जी 2 के पूरक लेना , आपके पास है -
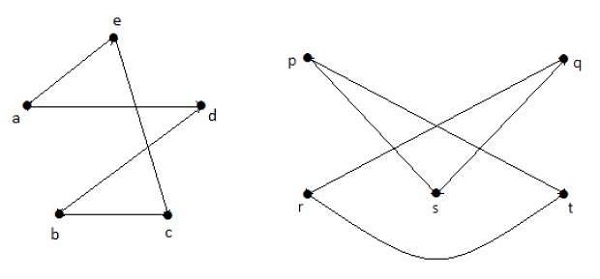
यहां, (जी 1 - 2 जी 2 -), इसलिए (जी 1 ) जी 2 )।
प्लेनर रेखांकन
एक ग्राफ 'जी' को प्लेनर कहा जाता है यदि इसे एक विमान या एक गोले पर खींचा जा सकता है ताकि कोई भी दो किनारे एक-दूसरे को गैर-शीर्ष बिंदु पर पार न करें।
Example
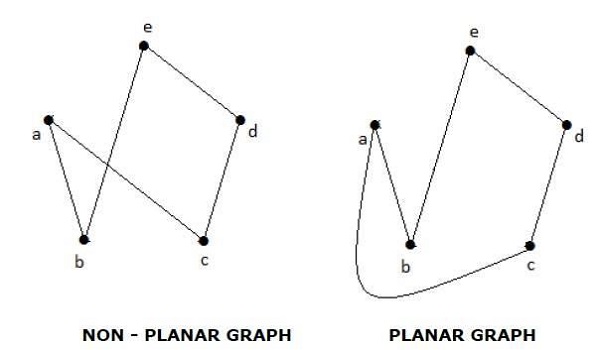
क्षेत्रों
प्रत्येक प्लानर ग्राफ विमान को संबंधित क्षेत्रों में विभाजित करता है जिन्हें क्षेत्र कहा जाता है।
Example
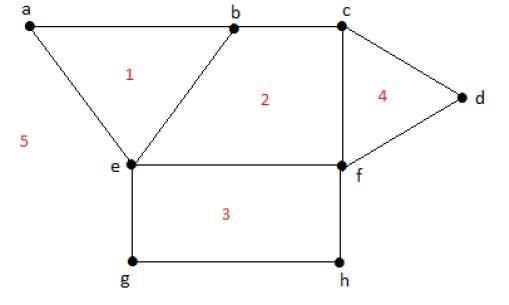
एक बंधे हुए क्षेत्र की डिग्री r = deg(r) क्षेत्रों को घेरने वाले किनारों की संख्या r।
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8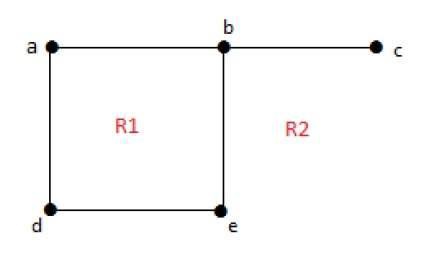
एक अनबिके क्षेत्र की डिग्री r = deg(r) क्षेत्रों को घेरने वाले किनारों की संख्या r।
deg(R1) = 4
deg(R2) = 6प्लानर रेखांकन में, निम्नलिखित गुण अच्छे हैं -
'N' वर्टिकल के साथ एक प्लैनर ग्राफ में, सभी वर्टिकल की डिग्री का योग है -
इसके अनुसार Sum of Degrees of Regions/ प्रमेय, 'एन' क्षेत्रों के साथ एक प्लैनर ग्राफ में, क्षेत्रों की डिग्री का योग है -
उपरोक्त प्रमेय के आधार पर, आप निम्नलिखित निष्कर्ष निकाल सकते हैं -
एक प्लैनर ग्राफ में,
यदि प्रत्येक क्षेत्र की डिग्री K है, तो क्षेत्रों की डिग्री का योग है -
यदि प्रत्येक क्षेत्र की डिग्री कम से कम K () K) है, तो
यदि प्रत्येक क्षेत्र की डिग्री अधिकांश K (, K) पर है, तो
Note - मान लें कि सभी क्षेत्रों में समान डिग्री है।
इसके अनुसार Euler’s Formulae प्लानर ग्राफ पर,
यदि एक ग्राफ 'जी' जुड़ा हुआ प्लानर है, तो
यदि 'के' घटकों के साथ एक प्लैनर ग्राफ, तो
जहाँ, | वी | वर्टिकल की संख्या है, | E | किनारों की संख्या है, और | R | क्षेत्रों की संख्या है।
एज वर्टेक्स असमानता
यदि 'G' कम से कम 'K' प्रत्येक क्षेत्र की डिग्री के साथ जुड़ा हुआ प्लानर ग्राफ है,
| E | ≤ के / ((-2) {| v | - 2}
तुम्हें पता है, | वी | + | आर | = | ई | + 2
लालकृष्ण | R | | 2 | ई |
K (| E | - | V | + 2) E 2 | E |
(के - 2) | ई | ≤ के (| वी | - २)
| E | ≤ के / ((-2) {| v | - 2}
यदि 'G' एक साधारण जुड़ा हुआ प्लानर ग्राफ है, तो
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4कम से कम एक वर्टेक्स वी • at जी मौजूद है, जैसे कि डाउन (वी) ver 5।
यदि 'G' एक साधारण जुड़ा हुआ प्लानर ग्राफ है (कम से कम 2 किनारों वाला) और कोई त्रिकोण नहीं है, तो
|E| ≤ {2|V| – 4}Kuratowski के प्रमेय
एक ग्राफ 'जी' नॉन-प्लानर है अगर और केवल अगर 'जी' में एक सबग्राफ है जो कि के 5 या के 3,3 के लिए होम्योमोर्फिक है ।
समरूपता
दो ग्राफ G 1 और G 2 को होमोमोर्फिक कहा जाता है, यदि इनमें से प्रत्येक ग्राफ को G के कुछ किनारों को अधिक चक्कर लगाकर एक ही ग्राफ 'G' से प्राप्त किया जा सकता है। निम्नलिखित उदाहरण पर एक नज़र डालें -

एक वर्टेक्स जोड़कर किनारे 'आरएस' को दो किनारों में विभाजित करें।
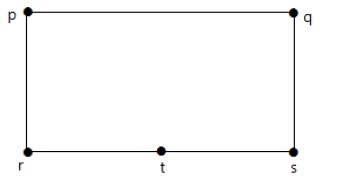
नीचे दिखाए गए रेखांकन पहले ग्राफ के समरूप हैं।
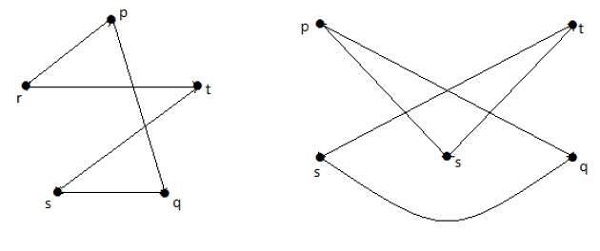
यदि जी 1 , जी 2 से आइसोमोर्फिक है , तो जी, जी 2 से होमियोमॉर्फिक है, लेकिन ऐंठन की आवश्यकता सच नहीं है।
4 या उससे कम लम्बाई वाला कोई भी ग्राफ़ प्लानर है।
8 या उससे कम किनारों वाला कोई भी ग्राफ़ प्लानर है।
एक पूरा ग्राफ K n प्लानर है अगर और केवल अगर n is 4।
पूरा द्विदलीय ग्राफ K m, n प्लानेर है और यदि केवल or 2 या n। 2 है तो।
न्यूनतम संख्या के साथ एक साधारण गैर-प्लानर ग्राफ पूरा ग्राफ K 5 है ।
न्यूनतम संख्या किनारों वाला सरल गैर-प्लानर ग्राफ K 3, 3 है ।
पॉलीहेड्रल ग्राफ
एक साधारण कनेक्टेड प्लानर ग्राफ को पॉलीहेड्रल ग्राफ कहा जाता है यदि प्रत्येक वर्टेक्स की डिग्री, 3 है, यानी, deg (V) V 3 ∈ V ∈ जी।
3 | वी | | 2 | ई |
3 | R | | 2 | ई |
यदि आप एक ही पथ को पुन: बनाए बिना सभी कोने के बीच एक मार्ग आकर्षित कर सकते हैं तो एक ग्राफ ट्रैवर्सेबल है। इस पथ के आधार पर, कुछ श्रेणियां हैं जैसे कि यूलर का मार्ग और यूलर का सर्किट जो इस अध्याय में वर्णित हैं।
यूलर का रास्ता
एक यूलर के रास्ते में 'G' के प्रत्येक किनारे में एक बार बिल्कुल और 'G' के प्रत्येक शीर्ष पर कम से कम एक बार होता है। एक जुड़ा हुआ ग्राफ जी को ट्रैवर्सेबल कहा जाता है यदि इसमें एक यूलर का रास्ता शामिल है।
Example
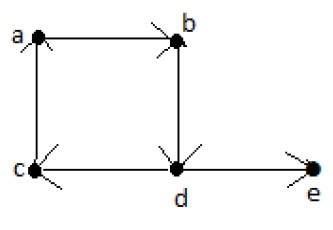
यूलर का रास्ता = dcabde।
यूलर का सर्किट
एक यूलर के मार्ग में, यदि शुरुआती शीर्ष उसकी समाप्ति शीर्ष रेखा के समान है, तो इसे यूलर सर्किट कहा जाता है।
Example
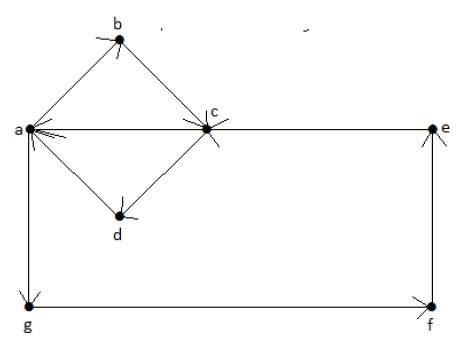
Euler’s Path = एबगैगफेका।
यूलर के सर्किट प्रमेय
एक जुड़ा ग्राफ 'जी' ट्रैवर्सिबल है यदि और केवल जी में विषम डिग्री के साथ कोने की संख्या ठीक 2 या 0. है तो कनेक्टेड ग्राफ जी में एक यूलर का पथ हो सकता है, लेकिन एक यूलर का सर्किट नहीं, अगर इसके साथ दो कोने हैं एक अजीब डिग्री।
Note - यह यूलर मार्ग विषम डिग्री के शीर्ष के साथ शुरू होता है और विषम डिग्री के अन्य शीर्ष के साथ समाप्त होता है।
Example
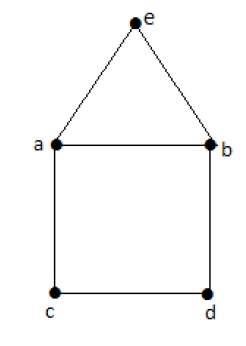
Euler’s Path- बीब्डका एक यूलर सर्किट नहीं है, लेकिन यह एक यूलर का रास्ता है। स्पष्ट रूप से इसमें 2 विषम डिग्री कोने हैं।
Note - एक जुड़े ग्राफ G में, यदि विषम डिग्री = 0 के साथ कोने की संख्या है, तो यूलर का सर्किट मौजूद है।
हैमिल्टनियन ग्राफ
एक जुड़ा हुआ ग्राफ जी को हैमिल्टनियन ग्राफ कहा जाता है, अगर कोई चक्र मौजूद होता है जिसमें G के सभी कोने होते हैं।
हर चक्र एक सर्किट है लेकिन एक सर्किट में कई चक्र हो सकते हैं। इस तरह के एक चक्र को कहा जाता हैHamiltonian cycle जी का।
हैमिल्टनियन पाथ
एक जुड़े ग्राफ को हैमिल्टनियन कहा जाता है यदि इसमें जी के प्रत्येक शीर्ष पर एक बार एक ही बार होता है। इस तरह के एक पथ को कहा जाता हैHamiltonian path।
Example
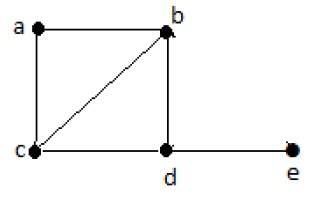
Hamiltonian Path- edbac।
Note
Euler के सर्किट में ग्राफ के प्रत्येक किनारे बिल्कुल एक बार होते हैं।
एक हैमिल्टनियन चक्र में, ग्राफ के कुछ किनारों को छोड़ दिया जा सकता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
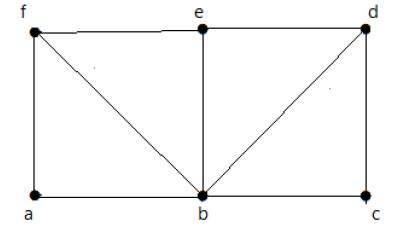
ऊपर दिखाए गए ग्राफ के लिए -
यूलर पथ मौजूद है - असत्य
यूलर सर्किट मौजूद है - असत्य
हैमिल्टनियन चक्र मौजूद है - सच
हैमिल्टन मार्ग मौजूद है - सत्य
जी में विषम डिग्री के साथ चार कोने हैं, इसलिए यह ट्रैवर्सेबल नहीं है। आंतरिक किनारों को लंघन करके, ग्राफ़ में एक हैमिल्टनियन चक्र है जो सभी कोने से गुजरता है।
इस अध्याय में, हम पहले से ही अध्यायों में चर्चा की गई अवधारणाओं को प्रदर्शित करने के लिए कुछ मानक उदाहरणों को कवर करेंगे।
उदाहरण 1
Find the number of spanning trees in the following graph.
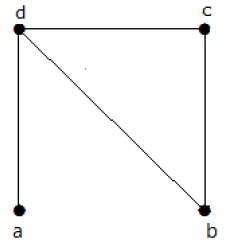
उपाय
उपरोक्त ग्राफ से प्राप्त फैले पेड़ों की संख्या 3. वे इस प्रकार हैं -
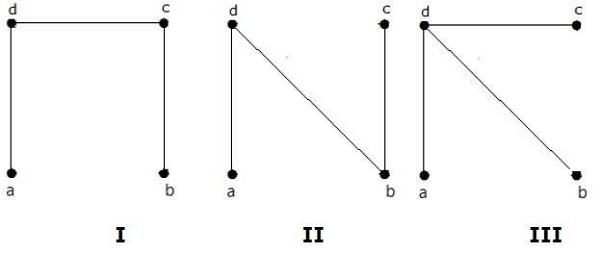
ये तीनों दिए गए रेखांकन के लिए फैले हुए पेड़ हैं। यहाँ ग्राफ I और II एक दूसरे के लिए समसामयिक हैं। स्पष्ट रूप से, गैर-आइसोमॉर्फिक फैले पेड़ों की संख्या दो है।
उदाहरण 2
How many simple non-isomorphic graphs are possible with 3 vertices?
उपाय
3 कोने के साथ 4 गैर-आइसोमॉर्फिक ग्राफ़ संभव हैं। उन्हें नीचे दिखाया गया है।
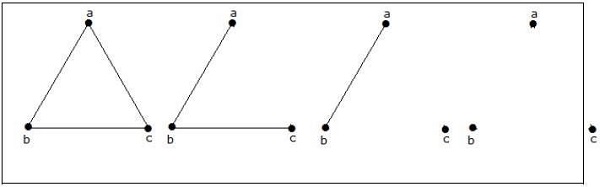
उदाहरण 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
उपाय
डिग्री प्रमेय के योग से,
२० 1 i = १ डिग (वि) = २ | ई |
२० (३) = २ | ई |
| E | = 30
Euler सूत्र द्वारा,
| वी | + | आर | = | ई | + 2
20+ | आर | = 30 + 2
| R | = 12
इसलिए, क्षेत्रों की संख्या 12 है।
उदाहरण 4
What is the chromatic number of complete graph Kn?
उपाय
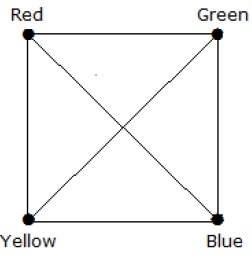
एक पूर्ण ग्राफ में, प्रत्येक शीर्ष समीप है (n-1) लंबवत है। इसलिए, प्रत्येक शीर्ष को एक नए रंग की आवश्यकता होती है। इसलिए वर्णिक संख्या K n = n है।
उदाहरण 5
What is the matching number for the following graph?
उपाय
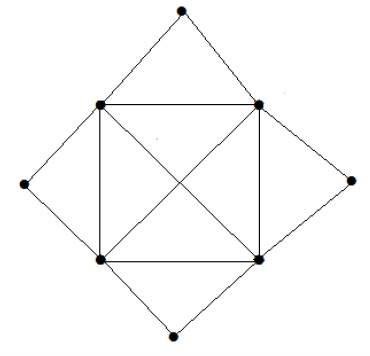
कोने की संख्या = 9
हम केवल 8 शीर्षकों का मिलान कर सकते हैं।
मिलान संख्या 4 है।
उदाहरण 6
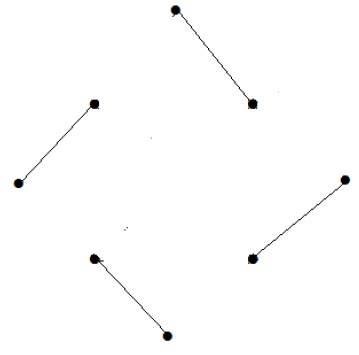
What is the line covering number of for the following graph?
उपाय
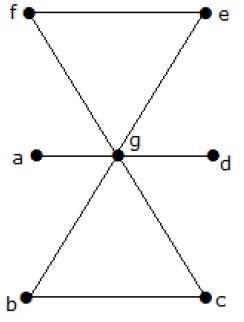
खांचों की संख्या = | वी | = एन = =
पंक्ति को कवर करने वाली संख्या = (α 1 ) [n / 2] = 3
α 1 α 3
3 किनारों का उपयोग करके, हम सभी कोने को कवर कर सकते हैं।
इसलिए, संख्या को कवर करने वाली रेखा 3 है।