ग्राफ सिद्धांत - पेड़
पेड़ ऐसे ग्राफ होते हैं जिनमें एक भी चक्र नहीं होता है। वे चित्रमय रूप में पदानुक्रमित संरचना का प्रतिनिधित्व करते हैं। पेड़ ग्राफ के सबसे सरल वर्ग के हैं। उनकी सादगी के बावजूद, उनके पास एक समृद्ध संरचना है।
पेड़ कंप्यूटर विज्ञान की डेटा संरचनाओं में पेड़ के रूप में जटिल के रूप में सरल के रूप में उपयोगी अनुप्रयोगों की एक श्रृंखला प्रदान करते हैं।
पेड़
ए connected acyclic graphवृक्ष कहलाता है। दूसरे शब्दों में, बिना किसी चक्र के जुड़े हुए ग्राफ को वृक्ष कहा जाता है।
एक पेड़ के किनारों के रूप में जाना जाता है branches। पेड़ों के तत्वों को उनके नोड्स कहा जाता है। बिना बच्चे के नोड्स को कहा जाता हैleaf nodes।
'N' वर्टीकल वाले पेड़ में 'n-1' किनारे होते हैं। यदि इसमें 'n-1' की तुलना में एक और बढ़त है, तो अतिरिक्त किनारे को स्पष्ट रूप से दो कोने के साथ जोड़ना होगा, जिससे एक चक्र बनता है। फिर, यह एक चक्रीय ग्राफ बन जाता है जो पेड़ के ग्राफ का उल्लंघन है।
Example 1
यहां दिखाया गया ग्राफ एक पेड़ है क्योंकि इसमें कोई चक्र नहीं है और यह जुड़ा हुआ है। परिभाषा में उल्लिखित 'एन' कोने 'एन -1' किनारों के लिए इसके चार कोने और तीन किनारे हैं।
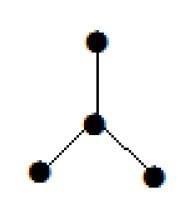
Note - प्रत्येक पेड़ में डिग्री एक के कम से कम दो कोने होते हैं।
Example 2
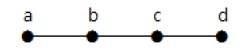
उपरोक्त उदाहरण में, शीर्षकों 'a' और 'd' में डिग्री एक है। और अन्य दो कोने 'बी' और 'सी' की डिग्री दो हैं। यह संभव है क्योंकि चक्र नहीं बनाने के लिए, ग्राफ़ में कहीं भी कम से कम दो एकल किनारे होने चाहिए। यह एक डिग्री के साथ दो किनारों के अलावा कुछ भी नहीं है।
वन
ए disconnected acyclic graphजंगल कहलाता है। दूसरे शब्दों में, पेड़ों के एक निराशाजनक संग्रह को जंगल कहा जाता है।
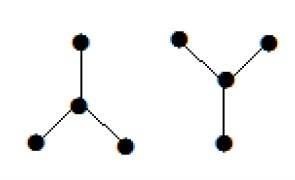
Example
निम्न ग्राफ़ दो उप-ग्राफ़ की तरह दिखता है; लेकिन यह एक एकल डिस्कनेक्ट ग्राफ है। इस ग्राफ में कोई चक्र नहीं हैं। इसलिए, स्पष्ट रूप से यह एक जंगल है।
फैलते हुए पेड़
मान लीजिए कि G एक जुड़ा हुआ ग्राफ़ है, तो G के उप-ग्राफ़ को G का एक फैले हुए वृक्ष कहा जाता है -
- एच एक पेड़ है
- H में G के सभी कोने हैं।
एक अप्रत्यक्ष ग्राफ G का एक फैला हुआ पेड़ T एक सबग्राफ है जिसमें G के सभी कोने शामिल हैं।
Example

उपरोक्त उदाहरण में, G एक जुड़ा हुआ ग्राफ है और H, G का उप-ग्राफ है।
स्पष्ट रूप से, ग्राफ एच में कोई चक्र नहीं है, यह छह किनारों वाला एक पेड़ है जो कुल संख्याओं की तुलना में कम है। इसलिए H, G का स्पानिंग ट्री है।
सर्किट रैंक
Let G ’को 'n’ कोने और edges m ’किनारों से जुड़ा ग्राफ होने दें। जी के एक फैले हुए वृक्ष 'T' में (n-1) किनारे होते हैं।
इसलिए, एक फैले हुए पेड़ = m- (n-1) को प्राप्त करने के लिए आपको किनारों की संख्या को 'G' से हटाना होगा, जिसे G की सर्किट रैंक कहा जाता है।
यह सूत्र सत्य है, क्योंकि एक फैले हुए वृक्ष में आपको 'एन -1' किनारों की आवश्यकता होती है। 'M' किनारों में से, आपको ग्राफ़ में 'n-1' किनारों को रखने की आवश्यकता है।
इसलिए, 'मी' से 'एन -1' किनारों को हटाने से किनारों को ग्राफ से हटा दिया जाता है ताकि एक फैले हुए पेड़ को प्राप्त किया जा सके, जिसे एक चक्र नहीं बनाना चाहिए।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
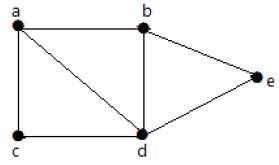
उपरोक्त उदाहरण में दिए गए ग्राफ़ के लिए, आपके पास m = 7 किनारे और n = 5 कोने हैं।
फिर सर्किट रैंक है -
Example
बता दें कि 'G' छह वर्टिकल के साथ एक जुड़ा हुआ ग्राफ है और प्रत्येक वर्टेक्स की डिग्री तीन है। 'G' का सर्किट रैंक ज्ञात कीजिए।
कार्यक्षेत्र प्रमेय की डिग्री के योग से,
किरचॉफ का प्रमेय
किरचॉफ का प्रमेय एक फैले हुए ग्राफ से बनने वाले पेड़ों की संख्या का पता लगाने में उपयोगी है।
Example
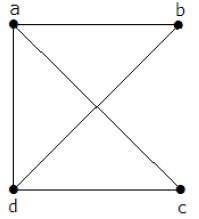
मैट्रिक्स 'ए' को भरा जाना चाहिए, यदि दो कोने के बीच एक धार है, तो इसे '1' के रूप में दिया जाना चाहिए, अन्यथा '0'।
$$ A = \ start {vmatrix} 0 & a & b & c & d \\ a & 0 & 1 & 1 & 1 \\ b & 1 & 0 & 0 & 1 \\ c & 1 & 1 & 0 & 0 & 1 \\ d & 1 & 1 & 1 & 1 \ n अंत {vmatrix} = \ {{vmatrix} 0 शुरू और 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \ end {vmatrix} $$किर्चॉफ के प्रमेय का उपयोग करके, इसे तिरछे डिग्री और अन्य सभी तत्वों के साथ सिद्धांत विकर्ण मानों को बदलने के रूप में बदला जाना चाहिए।
$$ = \ start {vmatrix} 3 और -1 और -1 & -1 \\ - 1 और 2 और 0 & -1 \\ - 1 और 0 और 2 और -1 \\ - 1 और -1 & -1 & 3 \ end {vmatrix} = M $$ $$ M = \ start {vmatrix} 3 और -1 और -1 & -1 \\ - 1 & 2 & 0 & -1 \\ - 1 और 0 & 2 & -1 \\ - 1 & -1 और -1 और 3 \ अंत {vmatrix} = 8 $ $ $ $ सह: \: कारक \: \ का: \: एम 1 \: \: = \ _ {vmatrix शुरू } 2 & 0 & -1 \\ 0 & 2 & -1 \\ - 1 और -1 & 3 \ अंत {vmatrix} $ $इस प्रकार, फैले पेड़ों की संख्या = 8।