ग्राफ सिद्धांत - रेखांकन के प्रकार
वर्टिकल की संख्या, किनारों की संख्या, इंटरकनेक्टिविटी और उनकी समग्र संरचना के आधार पर विभिन्न प्रकार के ग्राफ़ होते हैं। हम इस अध्याय में केवल कुछ महत्वपूर्ण प्रकार के रेखांकन पर चर्चा करेंगे।
नल का ग्राफ
A graph having no edges को Null Graph कहा जाता है।
उदाहरण

उपरोक्त ग्राफ में, 'a', 'b', और 'c' नाम के तीन वर्टीकल हैं, लेकिन उनमें कोई किनारा नहीं है। इसलिए यह एक नल ग्राफ है।
तुच्छ आलेख
ए graph with only one vertex एक तुच्छ ग्राफ कहा जाता है।
उदाहरण

ऊपर दिखाए गए ग्राफ़ में, केवल एक शीर्ष 'a' है जिसमें कोई दूसरा किनारा नहीं है। इसलिए यह एक तुच्छ ग्राफ है।
गैर-निर्देशित ग्राफ़
एक गैर-निर्देशित ग्राफ में किनारों होते हैं लेकिन किनारों को निर्देशित नहीं किया जाता है।
उदाहरण
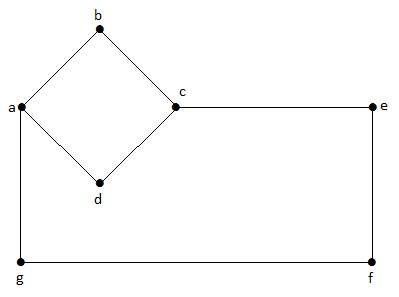
इस ग्राफ में, 'a', 'b', 'c', 'd', 'e', 'f', 'g' वर्टिकल हैं, और 'ab', 'bc', 'cd', 'da ',' एजी ',' जीएफ ',' एफई 'ग्राफ के किनारे हैं। चूंकि यह एक गैर-निर्देशित ग्राफ है, इसलिए किनारों 'अब' और 'बा' समान हैं। इसी तरह अन्य किनारों को भी उसी तरह से माना जाता है।
निर्देशित आलेख
एक निर्देशित ग्राफ में, प्रत्येक किनारे की एक दिशा होती है।
उदाहरण

उपरोक्त ग्राफ में, हमारे पास सात कोने 'ए', 'बी', 'सी', 'डी', 'ई', 'एफ', और 'जी' और 'एब्स', 'सीबी', '' हैं। dc ',' ad ',' ec ',' fe ',' gf ', और' ga '। जैसा कि यह एक निर्देशित ग्राफ है, प्रत्येक किनारे पर एक तीर का निशान होता है जो इसकी दिशा दिखाता है। ध्यान दें कि एक निर्देशित ग्राफ में, 'ab' 'ba' से अलग है।
सरल ग्राफ
एक ग्राफ with no loops और नहीं parallel edges एक साधारण ग्राफ कहा जाता है।
'N' वर्टिकल के साथ सिंगल ग्राफ में संभव किनारों की अधिकतम संख्या n C 2 है जहाँ n C 2 = n (n - 1/2) है।
'N' कोने = 2 n c 2 = 2 n (n-1) / 2 के साथ संभव सरल रेखांकन की संख्या ।
उदाहरण
निम्नलिखित ग्राफ़ में, 3 किनारों के साथ 3 कोने हैं जो समानांतर किनारों और छोरों को छोड़कर अधिकतम है। यह उपरोक्त सूत्रों का उपयोग करके साबित किया जा सकता है।
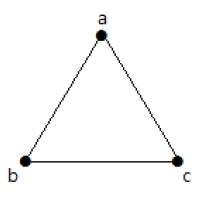
N = 3 कोने वाले किनारों की अधिकतम संख्या -
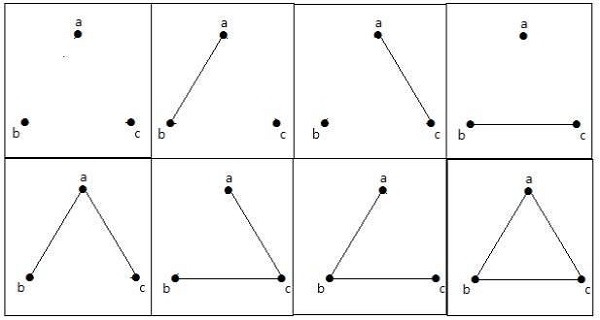
एन = 3 कोने के साथ सरल रेखांकन की अधिकतम संख्या -
ये 8 रेखांकन नीचे दिखाए गए हैं -
जुड़ा हुआ ग्राफ
एक ग्राफ G को जुड़ा हुआ कहा जाता है if there exists a path between every pair of vertices। ग्राफ में प्रत्येक शीर्ष के लिए कम से कम एक किनारे होना चाहिए। ताकि हम यह कह सकें कि यह किनारे के दूसरी तरफ किसी अन्य शीर्ष से जुड़ा है।
उदाहरण
निम्नलिखित ग्राफ में, प्रत्येक शीर्ष की अपनी बढ़त दूसरे किनारे से जुड़ी होती है। इसलिए यह एक जुड़ा हुआ ग्राफ है।

डिस्कनेक्ट किया गया ग्राफ़
एक ग्राफ जी काट दिया जाता है, अगर इसमें कम से कम दो जुड़े हुए कोने नहीं होते हैं।
उदाहरण 1
निम्नलिखित ग्राफ एक डिस्कनेक्ट किए गए ग्राफ़ का एक उदाहरण है, जहाँ दो घटक होते हैं, जिनमें से एक '' ए ',' बी ',' सी ',' डी 'वर्टिकल और दूसरा' ई ',' एफ ',' जी 'के साथ होता है। 'ज' वर्टिस।
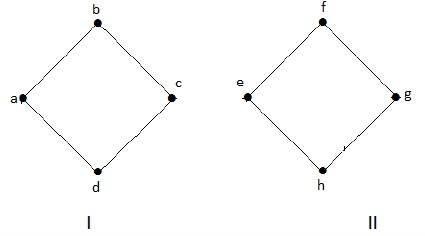
दो घटक स्वतंत्र हैं और एक दूसरे से जुड़े नहीं हैं। इसलिए इसे डिस्कनेक्ट ग्राफ कहा जाता है।
उदाहरण 2

इस उदाहरण में, दो स्वतंत्र घटक हैं, एब्फ़ और सीडी, जो एक दूसरे से जुड़े नहीं हैं। इसलिए यह एक डिस्कनेक्ट किया गया ग्राफ़ है।
नियमित ग्राफ
एक ग्राफ G को नियमित रूप से कहा जाता है, if all its vertices have the same degree। एक ग्राफ में, यदि प्रत्येक शीर्ष की डिग्री 'के' है, तो ग्राफ को 'के-रेगुलर ग्राफ' कहा जाता है।
उदाहरण
निम्नलिखित रेखांकन में, सभी कोने एक ही डिग्री के हैं। अतः इन रेखांकन को नियमित रेखांकन कहते हैं।
दोनों रेखांकन में, सभी लंबों की डिग्री 2 है। उन्हें 2-नियमित रेखांकन कहा जाता है।
पूरा ग्राफ
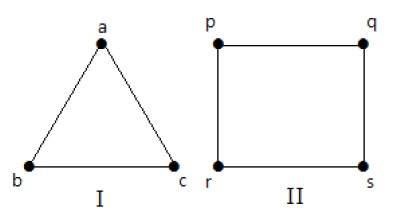
'एन' आपसी वर्टिकल वाले साधारण ग्राफ को पूर्ण ग्राफ कहा जाता है और यह है denoted by ‘Kn’। ग्राफ में,a vertex should have edges with all other vertices, तो यह एक पूरा ग्राफ कहा जाता है।
दूसरे शब्दों में, यदि एक ग्राफ में सभी शीर्षों को एक शीर्ष से जोड़ा जाता है, तो इसे पूर्ण ग्राफ़ कहा जाता है।
उदाहरण
निम्नलिखित ग्राफ़ में, ग्राफ़ के प्रत्येक शीर्ष को ग्राफ के सभी शेष शीर्षों के साथ जोड़ा जाता है, सिवाय इसके कि।
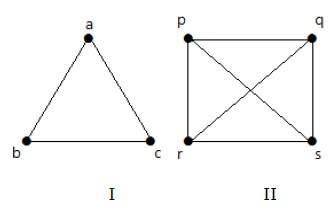
ग्राफ I में,
| ए | ख | सी | |
|---|---|---|---|
| ए | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए |
| ख | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए |
| सी | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं |
ग्राफ II में,
| पी | क्यू | आर | रों | |
|---|---|---|---|---|
| पी | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए | जुड़े हुए |
| क्यू | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए | जुड़े हुए |
| आर | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं | जुड़े हुए |
| रों | जुड़े हुए | जुड़े हुए | जुड़े हुए | जुड़े नहीं हैं |
साइकिल ग्राफ
'N' कोने (n> = 3) और 'n' किनारों वाले एक सरल ग्राफ को एक चक्र ग्राफ कहा जाता है यदि इसके सभी किनारों पर लंबाई 'n' का चक्र होता है।
यदि ग्राफ में प्रत्येक शीर्ष की डिग्री दो है, तो इसे साइकल ग्राफ कहा जाता है।
Notation- सी एन
उदाहरण
निम्नलिखित रेखांकन पर एक नज़र डालें -
ग्राफ I में 3 किनारों के साथ 3 कोने हैं जो एक चक्र 'अब-बीसी-सीए' बना रहा है।
ग्राफ II में 4 किनारों के साथ 4 कोने हैं जो एक चक्र 'pq-qs-sr-rp' बना रहा है।
ग्राफ III में 5 किनारों के साथ 5 कोने हैं जो एक चक्र 'ik-km-ml-lj-ji' बना रहा है।

इसलिए सभी दिए गए रेखांकन चक्र रेखांकन हैं।
व्हील ग्राफ
एक चक्र ग्राफ C n-1 से एक नया वर्टेक्स जोड़कर प्राप्त किया जाता है । उस नए शीर्ष को a कहा जाता हैHubजो C n के सभी कोने से जुड़ा हुआ है ।
संकेतन - डब्ल्यू एन
W n में किनारों की संख्या = हब से किनारों के अन्य सभी कोने तक +
हब के बिना साइकिल ग्राफ में अन्य सभी नोड्स से किनारों की संख्या।
= (n-1) + (n-1)
= 2 (एन -1)
उदाहरण
निम्नलिखित रेखांकन पर एक नज़र डालें। वे सभी व्हील ग्राफ हैं।
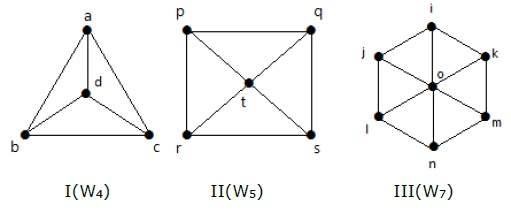
ग्राफ I में, इसे C 3 से 'd' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है । इसे W 4 के रूप में दर्शाया गया है ।
W4 = 2 (n-1) = 2 (3) = 6 में किनारों की संख्या
ग्राफ II में, इसे C4 से 't' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है। इसे W 5 के रूप में दर्शाया गया है ।
W5 = 2 (n-1) = 2 (4) = 8 में किनारों की संख्या
ग्राफ III में, इसे C 6 से 'o' नाम के मध्य में एक शीर्ष जोड़कर प्राप्त किया जाता है । इसे W 7 के रूप में दर्शाया गया है ।
W4 = 2 (n-1) = 2 (6) = 12 में किनारों की संख्या
चक्रीय ग्राफ
एक ग्राफ with at least one चक्र को चक्रीय ग्राफ कहा जाता है।
उदाहरण
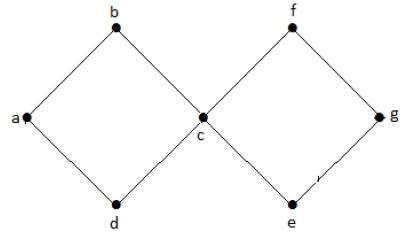
उपरोक्त उदाहरण के ग्राफ में, हमारे पास दो चक्र हैं abcda और cfgec। इसलिए इसे चक्रीय ग्राफ कहा जाता है।
चक्रीय ग्राफ
एक ग्राफ with no cycles एक चक्रीय ग्राफ कहलाता है।
उदाहरण
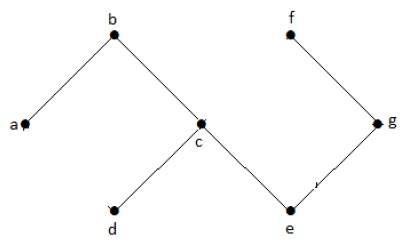
उपरोक्त उदाहरण के ग्राफ में, हमारे पास कोई चक्र नहीं है। इसलिए यह एक गैर-चक्रीय ग्राफ है।
द्विदलीय आलेख
एक साधारण ग्राफ G = (V, E) शीर्ष विभाजन के साथ V = {V 1 , V 2 } को द्विदलीय ग्राफ कहा जाता हैif every edge of E joins a vertex in V1 to a vertex in V2।
सामान्य तौर पर, एक Bipertite ग्राफ में दो सेट होते हैं, आइए हम कहते हैं, V1 और V2, और यदि एक किनारा खींचा जाता है, तो इसे सेट V 2 में किसी भी शीर्ष से किसी भी शीर्ष पर सेट V 2 में किसी भी शीर्ष से कनेक्ट करना चाहिए ।
उदाहरण
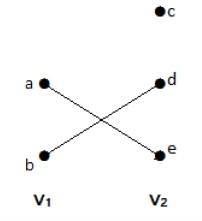
इस ग्राफ में, आप दो सेटों का अवलोकन कर सकते हैं - V 1 और V 2 । यहाँ, 'ae' और 'bd' नाम के दो किनारे दो सेट V 1 और V 2 के वर्टिकल को जोड़ रहे हैं ।
बिपर्टाइट ग्राफ को पूरा करें
एक द्विपक्षीय ग्राफ 'जी', जी = (वी, ई) विभाजन वी के साथ = {वी 1 , वी 2 } अगर वी में हर शिखर एक द्विपक्षीय ग्राफ की पूरी होना कहा जाता है 1 वी के हर शिखर से जुड़ा है 2 ।
सामान्य तौर पर, एक द्विपक्षीय ग्राफ की पूरी सेट वी से प्रत्येक शिखर जोड़ता है 1 सेट वी से प्रत्येक शीर्ष करने के लिए 2 ।
उदाहरण
क्योंकि यह सेट वी से प्रत्येक शिखर जोड़ने किनारों है निम्नलिखित ग्राफ एक द्विपक्षीय ग्राफ की पूरी है 1 सेट वी से प्रत्येक शीर्ष करने के लिए 2 ।
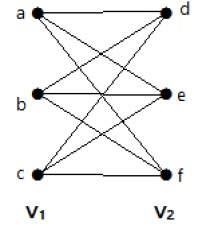
अगर - वी १ | = एम और वी 2 | = n, तो पूरा bipartite ग्राफ K m, n द्वारा निरूपित किया जाता है ।
- के एम, एन में (एम + एन) कोने और (एमएन) किनारों हैं।
- K m, n एक नियमित ग्राफ है यदि m = n।
सामान्य तौर पर, ए complete bipartite graph is not a complete graph।
K m, n एक पूर्ण ग्राफ है यदि m = n = 1।
एन कोने के साथ एक द्विदलीय ग्राफ में किनारों की अधिकतम संख्या है -
[एन २ / ४]
यदि n = 10, K5, 5 = [n2 / 4] = [10 2 /4] = 25।
इसी प्रकार, K6, 4 = 24
के 7, 3 = 21
के 8, 2 = 16
के 9, 1 = 9
यदि n = 9, k5, 4 = [n2 / 4] = [92/4] = 20
इसी प्रकार, K6, 3 = 18
के 7, 2 = 14
के 8, 1 = 8
यदि 'G' में विषम लंबाई का कोई चक्र नहीं है तो 'G' एक द्विदलीय ग्राफ है। द्विदलीय ग्राफ का एक विशेष मामला एक स्टार ग्राफ है।
स्टार ग्राफ
प्रपत्र K1, n-1 का एक पूर्ण द्विपद ग्राफ n-vertices के साथ एक स्टार ग्राफ है। एक स्टार ग्राफ एक पूर्ण द्विपदी ग्राफ है यदि एक एकल शीर्ष एक सेट से संबंधित है और सभी शेष कोने दूसरे सेट से संबंधित हैं।
उदाहरण
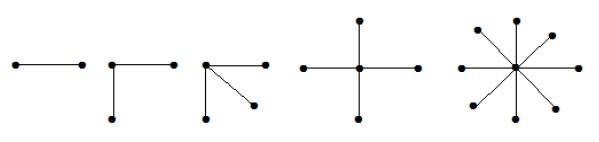
उपर्युक्त रेखांकन में, 'n' वर्टिकल में से, सभी 'n-1' वर्टिकल एक ही शीर्ष से जुड़े होते हैं। इसलिए यह K 1 , n-1 के रूप में है जो स्टार ग्राफ हैं।
एक ग्राफ का पूरक
'Gices' को 'G' के रूप में कुछ छोरों के साथ एक सरल ग्राफ होने दें और एक बढ़त {U, V} 'G present' में मौजूद है, यदि धार G. में मौजूद नहीं है, तो इसका मतलब है, दो कोने समीप हैं 'G ad' में यदि दो कोने G में समीप नहीं हैं।
यदि ग्राफ़ में मौजूद किनारों को दूसरे ग्राफ़ II में अनुपस्थित किया जाता है, और यदि ग्राफ़ I और ग्राफ़ II दोनों को एक साथ जोड़कर एक पूर्ण ग्राफ़ बनाया जाता है, तो ग्राफ़ I और ग्राफ़ II को एक दूसरे के पूरक कहा जाता है।
उदाहरण
निम्नलिखित उदाहरण में, ग्राफ- I में दो किनारों 'सीडी' और 'बीडी' हैं। इसके पूरक ग्राफ- II में चार किनारे हैं।
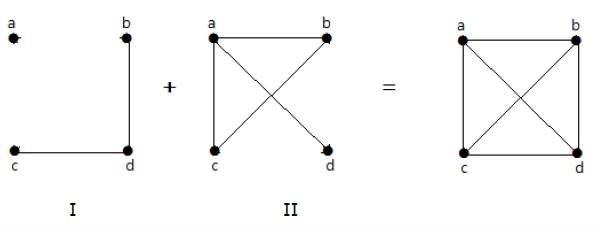
ध्यान दें कि ग्राफ- I में किनारों ग्राफ II और इसके विपरीत में मौजूद नहीं हैं। इसलिए, दोनों ग्राफों का संयोजन 'एन' वर्टिकल का पूरा ग्राफ देता है।
Note - दो पूरक रेखांकन का एक पूरा ग्राफ देता है।
यदि If जी ’कोई सरल ग्राफ है, तो
| ई (G) | + | ई ('जी -') | = | E (Kn) |, जहाँ n = ग्राफ़ में संख्याओं की संख्या।
उदाहरण
'' जी '' को '' नौ '' और बारह किनारों के साथ एक सरल ग्राफ होने दें, 'G-' में किनारों की संख्या ज्ञात करें।
आपके पास है।, E (G) | + | ई ('जी -') | = | ई (एनएन) |
12 + | ई ('जी -') | =
9 (9-1) / 2 = 9 सी 2
12 + | ई ('जी -') | = 36
| ई ( 'जी -') | = 24
'G' 40 किनारों वाला एक सरल ग्राफ है और इसके पूरक 'G has' में 38 किनारे हैं। ग्राफ G या 'G।' में लंबों की संख्या ज्ञात कीजिए।
बता दें कि ग्राफ में वर्टिकल की संख्या 'n' है।
हमारे पास, | ई (जी) | + | ई ('जी -') | = | ई (एनएन) |
40 + 38 = एन (एन -1) / 2
156 = एन (एन -1)
13 (12) = एन (एन -1)
n = 13