ग्राफ थ्योरी - कवरिंग
एक कवरिंग ग्राफ एक सबग्राफ है जिसमें किसी भी अन्य ग्राफ के अनुरूप सभी कोने या सभी किनारे होते हैं। एक सबग्राफ जिसमें सभी कोने होते हैं, a कहलाता हैline/edge covering। एक सबग्राफ जिसमें सभी किनारे होते हैं, a कहलाता हैvertex covering।
लाइन कवरिंग
G = (V, E) को एक ग्राफ बनाते हैं। एक सबसेट C (E) को G की एक कवर रेखा कहा जाता है यदि G के प्रत्येक शीर्ष पर C, यानी C में कम से कम एक किनारे के साथ घटना है
deg (V) ≥ 1 ∈ V V जी
क्योंकि प्रत्येक शीर्ष एक किनारे से दूसरे शीर्ष के साथ जुड़ा हुआ है। इसलिए इसकी न्यूनतम 1 डिग्री है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
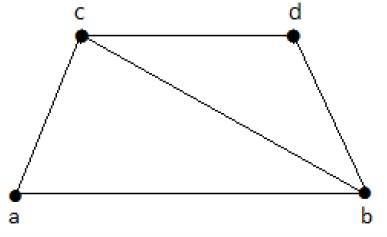
इसके सबग्राफ में लाइन कवरिंग निम्नानुसार हैं -
सी 1 = {{ए, बी}, {सी, डी}}
सी 2 = {{ए, डी}, {बी, सी}}
सी 3 = {{ए, बी}, {बी, सी}, {बी, डी}}
सी 4 = {{ए, बी}, {बी, सी}, {सी, डी}}
'G' की लाइन कवरिंग मौजूद नहीं है अगर और केवल 'G' में एक अलग वर्टेक्स हो। रेखांकन को 'n' वर्टिकल के साथ कवर करने के लिए कम से कम [n / 2] किनारों की आवश्यकता होती है।
मिनिमल लाइन कवरिंग
एक ग्राफ G के C को कवर करने वाली एक लाइन को न्यूनतम कहा जाता है if no edge can be deleted from C।
Example
उपर्युक्त ग्राफ में, लाइन को कवर करने वाले सबग्राफ निम्नानुसार हैं -
सी 1 = {{ए, बी}, {सी, डी}}
सी 2 = {{ए, डी}, {बी, सी}}
सी 3 = {{ए, बी}, {बी, सी}, {बी, डी}}
सी 4 = {{ए, बी}, {बी, सी}, {सी, डी}}
यहां, C 1 , C 2 , C 3 न्यूनतम लाइन कवरिंग हैं, जबकि C 4 इसलिए नहीं है क्योंकि हम {b, c} को हटा सकते हैं।
न्यूनतम लाइन कवरिंग
इसे के रूप में भी जाना जाता है Smallest Minimal Line Covering। न्यूनतम संख्या किनारों के साथ कवर करने वाली एक न्यूनतम रेखा को 'जी' की न्यूनतम रेखा को कवर किया जाता है। 'G' में न्यूनतम रेखा को कवर करने वाले किनारों की संख्या को कहा जाता हैline covering numberof 'G' (α 1 )।
Example
उपरोक्त उदाहरण में, सी 1 और सी 2 जी और α 1 = 2 को कवर करने वाली न्यूनतम रेखा है ।
हर लाइन कवरिंग में एक न्यूनतम लाइन कवरिंग होती है।
हर लाइन कवर में न्यूनतम लाइन कवरिंग नहीं होती है (C 3 में कोई न्यूनतम लाइन कवरिंग नहीं होती है।
कोई न्यूनतम पंक्ति कवर में एक चक्र नहीं होता है।
यदि 'C' को कवर करने वाली रेखा में लंबाई 3 या अधिक का कोई पथ नहीं है, तो 'C' एक न्यूनतम रेखा है, क्योंकि 'C' के सभी घटक स्टार ग्राफ हैं और स्टार ग्राफ से, कोई भी किनारा नहीं हटाया जा सकता है।
वर्टेक्स कवरिंग
चलो 'जी' = (वी, ई) एक ग्राफ हो। V के एक उपसमूह K को 'G' का एक शीर्ष आवरण कहा जाता है, यदि 'G' के प्रत्येक किनारे पर 'K' में एक शीर्ष रेखा के साथ घटना या आवरण होता है।
Example
निम्नलिखित ग्राफ पर एक नज़र डालें -
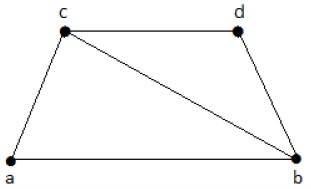
उपर्युक्त ग्राफ़ से प्राप्त किए जा सकने वाले उपसमूह इस प्रकार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}
K 4 = {a, d}
यहां, K 1 , K 2 , और K 3 में वर्टेक्स कवरिंग है, जबकि K 4 में कोई वर्टेक्स कवर नहीं है क्योंकि यह एज {bc} को कवर नहीं करता है।
न्यूनतम वर्टेक्स कवरिंग
ग्राफ 'जी' के एक शीर्ष 'के' को न्यूनतम कवर कहा जाता है यदि कोई शीर्ष को 'के' से हटाया नहीं जा सकता है।
Example
उपर्युक्त ग्राफ में, शीर्ष आवरण वाले उपसमूह निम्नानुसार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}
यहां, K 1 और K 2 न्यूनतम वर्टिकल कवरिंग हैं, जबकि K 3 में , वर्टेक्स 'd' को हटाया जा सकता है।
न्यूनतम वर्टेक्स कवरिंग
इसे सबसे छोटी न्यूनतम शीर्ष आवरण के रूप में भी जाना जाता है। न्यूनतम संख्या शीर्ष वाले ग्राफ 'G' के कवर को न्यूनतम वर्टेक्स कवरिंग कहा जाता है।
'G' के न्यूनतम वर्टेस्कल कवरिंग में वर्टिस की संख्या को G (α 2 ) की वर्टिकल कवरिंग संख्या कहा जाता है ।
Example
निम्नलिखित ग्राफ में, शीर्ष कवर करने वाले उपसमूह निम्नानुसार हैं -
के 1 = {बी, सी}
के 2 = {ए, बी, सी}
के 3 = {बी, सी, डी}

यहां, K 1 , G का एक न्यूनतम शीर्ष कवर है, क्योंकि इसमें केवल दो वर्टीकल हैं। α 2 = 2।