ग्राफ सिद्धांत - बुनियादी बातों
एक ग्राफ बिंदुओं और रेखाओं से जुड़ा हुआ रेखाचित्र है। इसमें कम से कम एक लाइन होती है, जिसमें दो वर्टीकल का एक सेट होता है, जिसमें कोई भी शीर्ष नहीं होता है। ग्राफ सिद्धांत में रेखांकन की अवधारणा कुछ मूल शब्दों पर निर्भर करती है जैसे बिंदु, रेखा, शीर्ष, धार, कोणों की डिग्री, रेखांकन के गुण, इत्यादि। इस अध्याय में, हम ग्राफ सिद्धांत के इन मूल सिद्धांतों को शामिल करेंगे।
बिंदु
A pointएक आयामी, दो आयामी या तीन आयामी अंतरिक्ष में एक विशेष स्थिति है। बेहतर समझ के लिए, एक बिंदु को एक वर्णमाला द्वारा निरूपित किया जा सकता है। इसे डॉट के साथ दर्शाया जा सकता है।
उदाहरण

यहाँ, बिंदु 'a' नाम का एक बिंदु है।
लाइन
ए Lineदो बिंदुओं के बीच एक संबंध है। इसे एक ठोस रेखा के साथ दर्शाया जा सकता है।
Example

यहाँ, 'ए' और 'बी' अंक हैं। इन दो बिंदुओं के बीच की कड़ी को एक रेखा कहा जाता है।
शिखर
एक शीर्ष बिंदु एक बिंदु है जहां कई लाइनें मिलती हैं। इसे ए भी कहा जाता हैnode। अंकों के समान, एक वर्णमाला भी एक वर्णमाला द्वारा निरूपित की जाती है।
Example

यहां, शीर्ष को वर्णमाला 'ए' के साथ नामित किया गया है।
एज
एक किनारे एक रेखा के लिए गणितीय शब्द है जो दो कोने जोड़ता है। एक किनारे से कई किनारों का निर्माण किया जा सकता है। एक शीर्ष के बिना, एक किनारे का गठन नहीं किया जा सकता है। एक आरंभिक शीर्ष और एक छोर के लिए एक अंतिम शीर्ष होना चाहिए।
Example

यहाँ, 'a' और 'b' दो कोने हैं और उनके बीच की कड़ी को किनारे कहा जाता है।
ग्राफ़
एक ग्राफ 'जी' को जी = (वी, ई) के रूप में परिभाषित किया गया है, जहां वी सभी लंबों का एक सेट है और ई ग्राफ में सभी किनारों का एक सेट है।
Example 1

उपरोक्त उदाहरण में, ab, ac, cd, और bd ग्राफ के किनारे हैं। इसी तरह, ए, बी, सी और डी ग्राफ के कोने हैं।
Example 2
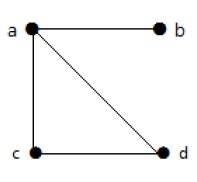
इस ग्राफ में, चार कोने हैं a, b, c, और d, और चार किनारों ab, ac, ad, और cd।
लूप
एक ग्राफ में, यदि एक किनारे को शीर्ष से स्वयं तक खींचा जाता है, तो इसे लूप कहा जाता है।
Example 1

उपर्युक्त ग्राफ में, वी एक शीर्ष है जिसके लिए एक छोर (वी, वी) एक लूप बनाता है।
Example 2

इस ग्राफ में, दो छोरें हैं जो कि वर्टेक्स ए, और वर्टेक्स बी पर बनती हैं।
वर्टेक्स की डिग्री
यह एक शीर्ष V से सटे कोने की संख्या है।
Notation - deg (V)।
किसी भी कोने की डिग्री के साथ सरल ग्राफ में, किसी भी कोने की डिग्री है -
deg (v) - n - 1 v v ≤ जी
एक शीर्ष अपने आप को छोड़कर सभी अन्य कोने के साथ एक बढ़त बना सकता है। तो एक शीर्ष की डिग्री तक हो जाएगाnumber of vertices in the graph minus 1। यह 1 स्वयं-शीर्ष के लिए है क्योंकि यह स्वयं एक लूप नहीं बना सकता है। यदि किसी भी कोने पर एक लूप है, तो यह एक सरल ग्राफ़ नहीं है।
ग्राफ के दो मामलों के तहत शीर्ष की डिग्री पर विचार किया जा सकता है -
अप्रत्यक्ष ग्राफ़
निर्देशित आलेख
अप्रत्यक्ष ग्राफ़ में वर्टेक्स की डिग्री
एक अप्रत्यक्ष ग्राफ़ में कोई निर्देशित किनारा नहीं है। निम्नलिखित उदाहरणों पर विचार करें।
Example 1
निम्नलिखित ग्राफ पर एक नज़र डालें -

उपरोक्त अप्रत्यक्ष ग्राफ़ में,
नीचे (ए) = 2, क्योंकि शीर्ष पर 2 किनारों की बैठक 'a' है।
deg (b) = 3, क्योंकि शीर्ष पर 3 किनारों की बैठकें 'b' हैं।
नीचे (c) = 1, क्योंकि शीर्ष पर 1 किनारे का गठन 'c' है
तो 'ग' एक है pendent vertex।
नीचे (d) = 2, क्योंकि शीर्ष पर 2 किनारों की बैठक 'd' है।
deg (e) = 0, क्योंकि शीर्ष पर 'e' में 0 किनारे बने होते हैं।
तो 'ई' एक है isolated vertex।
Example 2
निम्नलिखित ग्राफ पर एक नज़र डालें -

उपरोक्त ग्राफ में,
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2, and deg (e) = 0)।
शीर्ष 'ई ’एक पृथक शीर्ष है। ग्राफ में कोई पेंडेंट शीर्ष नहीं है।
एक निर्देशित ग्राफ में वर्टेक्स की डिग्री
एक निर्देशित ग्राफ में, प्रत्येक शीर्ष पर एक है indegree और एक outdegree।
एक ग्राफ की Indegree
वर्टेक्स V की इंद्रीरी किनारों की संख्या है जो वर्टेक्स V में आ रही हैं।
Notation - deg - (V)।
एक रेखांकन की रूपरेखा
वर्टेक्स V का आउटड्री उन किनारों की संख्या है जो वर्टेक्स V से निकल रहे हैं।
Notation - deg + (V)।
निम्नलिखित उदाहरणों पर विचार करें।
Example 1
निम्नलिखित निर्देशित ग्राफ पर एक नज़र डालें। वर्टेक्स 'ए' के दो किनारे हैं, 'ऐड' और 'एब', जो बाहर की ओर जा रहे हैं। इसलिए इसकी रूपरेखा 2 है। इसी प्रकार, एक किनारे 'गा' है, जो 'a' की ओर आ रहा है। अत: 'a' की इंद्री 1 है।

अन्य शीर्षकों की इंद्री और आउटड्री निम्नलिखित तालिका में दिखाए गए हैं -
| शिखर | Indegree | Outdegree |
|---|---|---|
| ए | 1 | 2 |
| ख | 2 | 0 |
| सी | 2 | 1 |
| घ | 1 | 1 |
| इ | 1 | 1 |
| च | 1 | 1 |
| जी | 0 | 2 |
Example 2
निम्नलिखित निर्देशित ग्राफ पर एक नज़र डालें। वर्टेक्स 'ए' में एक किनारे 'ए' है जो कि 'ए' से बाहर की ओर जा रहा है। इसलिए इसकी रूपरेखा 1 है। इसी तरह, ग्राफ में बढ़त 'बा' है जो 'शीर्ष' की ओर आ रही है। अत: 'a' की इंद्री 1 है।

अन्य शीर्षकों की इंद्री और आउटड्री निम्नलिखित तालिका में दिखाए गए हैं -
| शिखर | Indegree | Outdegree |
|---|---|---|
| ए | 1 | 1 |
| ख | 0 | 2 |
| सी | 2 | 0 |
| घ | 1 | 1 |
| इ | 1 | 1 |
पेंडेंट वर्टेक्स
एक वर्टेक्स की डिग्री का उपयोग करके, हमारे पास दो विशेष प्रकार के कोने हैं। डिग्री एक के साथ एक शीर्ष को पेंडेंट शीर्ष कहा जाता है।
Example

यहाँ, इस उदाहरण में, वर्टेक्स 'ए' और वर्टेक्स 'बी' का कनेक्टेड एज 'एब' है। तो 'a ’के संबंध में, b b’ की ओर केवल एक किनारा है और इसी तरह' b ’के संबंध में, tex a’ के संबंध में केवल एक ही किनारा है, 'a ’के लिए केवल एक ही किनारा है। अंत में, वर्टेक्स 'ए' और वर्टेक्स 'बी' के पास एक डिग्री है जिसे पेंडेंट वर्टेक्स भी कहा जाता है।
अलग-थलग
डिग्री शून्य के साथ एक शीर्ष को एक पृथक शीर्ष कहा जाता है।
Example

यहाँ, शीर्ष 'a' और vertex 'b' की आपस में कोई कनेक्टिविटी नहीं है और किसी अन्य कोने में भी है। अतः '' ए 'और' बी 'दोनों के अंश शून्य हैं। इन्हें आइसोलेटेड वर्टिकल भी कहा जाता है।
समीपता
यहाँ आसन्न के मानदंड हैं -
एक रेखांकन में, दो सिरों को कहा जाता है adjacent, अगर दो कोने के बीच एक धार है। यहाँ, उन दो सिरों को जोड़ने वाले एकल किनारे द्वारा कोने की आसन्नता बनाए रखी जाती है।
एक ग्राफ़ में, दो किनारों को आसन्न कहा जाता है, अगर दो किनारों के बीच एक सामान्य शीर्ष है। यहां, किनारों की निकटता को एकल शीर्ष द्वारा बनाए रखा जाता है जो दो किनारों को जोड़ रहा है।
Example 1
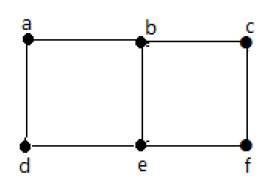
उपरोक्त ग्राफ में -
'a' और 'b' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'ab' है।
'a' और 'd' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'विज्ञापन' है।
ab 'और' be 'आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष' b 'है।
होना 'और' डे 'आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष' ई 'है।
Example 2
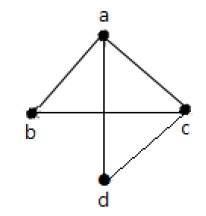
उपरोक्त ग्राफ में -
'a' और 'd' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'विज्ञापन' है।
'c' और 'b' आसन्न कोने हैं, क्योंकि उनके बीच एक सामान्य बढ़त 'cb' है।
'विज्ञापन' और 'सीडी' आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष 'डी' है।
'एसी' और 'सीडी' आसन्न किनारे हैं, क्योंकि उनके बीच एक सामान्य शीर्ष 'सी' है।
समानांतर किनारे
एक ग्राफ में, यदि एक जोड़े को एक से अधिक किनारों से जोड़ा जाता है, तो उन किनारों को समानांतर किनारे कहा जाता है।
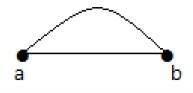
उपरोक्त ग्राफ में, 'a' और 'b' दो वर्टिकल हैं जो कि दो किनारों 'ab' और उनके बीच 'ab' से जुड़े हैं। तो यह एक समानांतर किनारे के रूप में कहा जाता है।
मल्टी ग्राफ
समानांतर किनारों वाले एक ग्राफ को मल्टीग्राफ के रूप में जाना जाता है।
Example 1

उपर्युक्त ग्राफ में, पाँच किनारे हैं 'अब', 'एसी', 'सीडी', 'सीडी' और 'बीडी'। चूँकि 'c' और 'd' के बीच दो समानांतर किनारे हैं, यह एक मल्टीग्राफ है।
Example 2
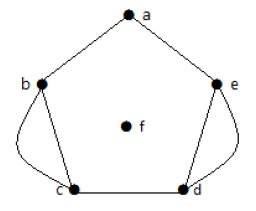
उपरोक्त ग्राफ में, 'बी' और 'सी' के दो किनारे हैं। शीर्ष 'ई' और 'डी' के बीच भी दो किनारे हैं। इसलिए यह एक मल्टीग्राफ है।
एक ग्राफ की डिग्री अनुक्रम
यदि किसी ग्राफ में सभी कोणों की डिग्री को अवरोही या आरोही क्रम में व्यवस्थित किया जाता है, तो प्राप्त अनुक्रम को ग्राफ के डिग्री अनुक्रम के रूप में जाना जाता है।
Example 1

| शिखर | ए | ख | सी | घ | इ |
|---|---|---|---|---|---|
| को जोड़ रहा | बी, सी | ए, डी | ए, डी | सी, बी, ई | घ |
| डिग्री | 2 | 2 | 2 | 3 | 1 |
उपरोक्त ग्राफ में, कोने {d, a, b, c, e} के लिए, डिग्री अनुक्रम {3, 2, 2, 2, 1} है।
Example 2

| शिखर | ए | ख | सी | घ | इ | च |
|---|---|---|---|---|---|---|
| को जोड़ रहा | ख, ई | एसी | बी, डी | सी, ई | ए, डी | - |
| डिग्री | 2 | 2 | 2 | 2 | 2 | 0 |
उपरोक्त ग्राफ में, कोने {{a, b, c, d, e, f}, के लिए डिग्री अनुक्रम {2, 2, 2, 2, 2, 0} है।