ग्राफ सिद्धांत - उदाहरण
इस अध्याय में, हम पहले से ही अध्यायों में चर्चा की गई अवधारणाओं को प्रदर्शित करने के लिए कुछ मानक उदाहरणों को कवर करेंगे।
उदाहरण 1
Find the number of spanning trees in the following graph.
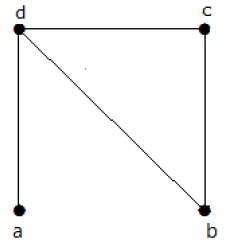
उपाय
उपरोक्त ग्राफ से प्राप्त फैले पेड़ों की संख्या 3. वे इस प्रकार हैं -
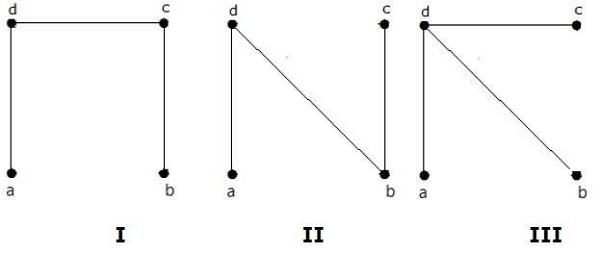
ये तीनों दिए गए रेखांकन के लिए फैले हुए पेड़ हैं। यहाँ ग्राफ I और II एक दूसरे के लिए समसामयिक हैं। स्पष्ट रूप से, गैर-आइसोमॉर्फिक फैले पेड़ों की संख्या दो है।
उदाहरण 2
How many simple non-isomorphic graphs are possible with 3 vertices?
उपाय
3 कोने के साथ 4 गैर-आइसोमॉर्फिक ग्राफ़ संभव हैं। उन्हें नीचे दिखाया गया है।
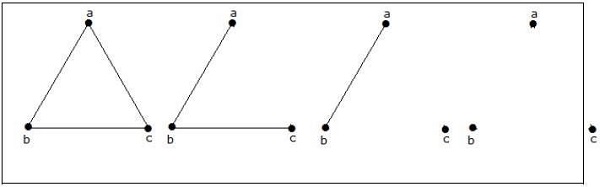
उदाहरण 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
उपाय
डिग्री प्रमेय के योग से,
२० 1 i = १ डिग (वि) = २ | ई |
२० (३) = २ | ई |
| E | = 30
Euler सूत्र द्वारा,
| वी | + | आर | = | ई | + 2
20+ | आर | = 30 + 2
| R | = 12
इसलिए, क्षेत्रों की संख्या 12 है।
उदाहरण 4
What is the chromatic number of complete graph Kn?
उपाय
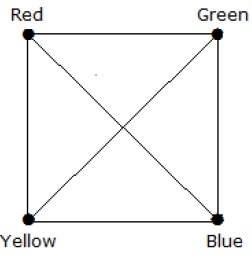
एक पूर्ण ग्राफ में, प्रत्येक शीर्ष समीप है (n-1) लंबवत है। इसलिए, प्रत्येक शीर्ष को एक नए रंग की आवश्यकता होती है। इसलिए वर्णिक संख्या K n = n है।
उदाहरण 5
What is the matching number for the following graph?
उपाय
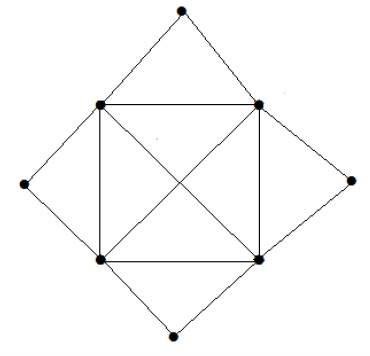
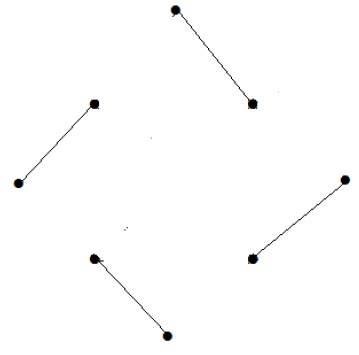
कोने की संख्या = 9
हम केवल 8 शीर्षकों का मिलान कर सकते हैं।
मिलान संख्या 4 है।
उदाहरण 6
What is the line covering number of for the following graph?
उपाय
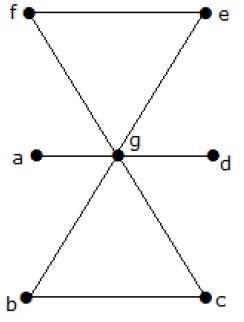
खांचों की संख्या = | वी | = एन = =
पंक्ति को कवर करने वाली संख्या = (α 1 ) [n / 2] = 3
α 1 α 3
3 किनारों का उपयोग करके, हम सभी कोने को कवर कर सकते हैं।
इसलिए, संख्या को कवर करने वाली रेखा 3 है।