Transformasi 2D
Transformasi berarti mengubah beberapa grafik menjadi sesuatu yang lain dengan menerapkan aturan. Kita dapat memiliki berbagai jenis transformasi seperti translasi, penskalaan ke atas atau ke bawah, rotasi, geser, dll. Ketika transformasi terjadi pada bidang 2D, itu disebut transformasi 2D.
Transformasi memainkan peran penting dalam grafik komputer untuk mengubah posisi grafik di layar dan mengubah ukuran atau orientasinya.
Koordinat Homogen
Untuk melakukan urutan transformasi seperti translasi diikuti dengan rotasi dan penskalaan, kita perlu mengikuti proses sekuensial -
- Terjemahkan koordinatnya,
- Putar koordinat yang diterjemahkan, lalu
- Skala koordinat yang diputar untuk menyelesaikan transformasi komposit.
Untuk mempersingkat proses ini, kita harus menggunakan matriks transformasi 3 × 3, bukan matriks transformasi 2 × 2. Untuk mengubah matriks 2 × 2 menjadi matriks 3 × 3, kita harus menambahkan koordinat dummy ekstra W.
Dengan cara ini, kita dapat merepresentasikan titik dengan 3 angka, bukan 2 angka, yang disebut Homogenous Coordinatesistem. Dalam sistem ini, kita dapat merepresentasikan semua persamaan transformasi dalam perkalian matriks. Setiap titik Cartesian P (X, Y) dapat diubah menjadi koordinat homogen dengan P '(X h , Y h , h).
Terjemahan
Terjemahan memindahkan objek ke posisi berbeda di layar. Anda dapat menerjemahkan sebuah titik dalam 2D dengan menambahkan koordinat terjemahan (t x , t y ) ke koordinat awal (X, Y) untuk mendapatkan koordinat baru (X ', Y').
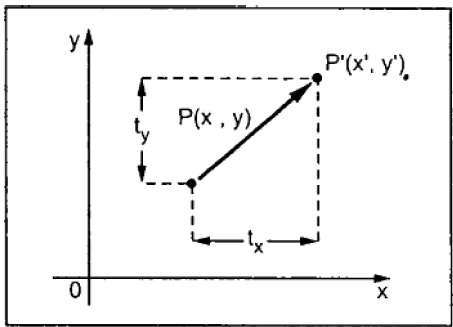
Dari gambar di atas, Anda dapat menulis bahwa -
X’ = X + tx
Y’ = Y + ty
Pasangan (t x , t y ) disebut vektor translasi atau vektor pergeseran. Persamaan di atas juga dapat direpresentasikan menggunakan vektor kolom.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
Kita bisa menulisnya sebagai -
P’ = P + T
Rotasi
Dalam rotasi, kami memutar objek pada sudut tertentu θ (theta) dari asalnya. Dari gambar berikut, kita dapat melihat bahwa titik P (X, Y) terletak pada sudut coordin dari koordinat X horizontal dengan jarak r dari titik asal.
Misalkan Anda ingin memutarnya pada sudut θ. Setelah memutarnya ke lokasi baru, Anda akan mendapatkan titik baru P '(X', Y ').

Menggunakan trigonometri standar, koordinat asli dari titik P (X, Y) dapat direpresentasikan sebagai -
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
Dengan cara yang sama kita dapat merepresentasikan titik P '(X', Y ') sebagai -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $
Mensubstitusikan persamaan (1) & (2) di (3) & (4) masing-masing, kita akan mendapatkan
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
Merepresentasikan persamaan di atas dalam bentuk matriks,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OR $$
P '= P. R
Dimana R adalah matriks rotasi
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
Sudut rotasi bisa positif dan negatif.
Untuk sudut rotasi positif, kita dapat menggunakan matriks rotasi di atas. Namun, untuk rotasi sudut negatif, matriks akan berubah seperti gambar di bawah ini -
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ karena cos (- \ theta) = cos \ theta \; dan \; sin (- \ theta) = −sin \ theta \ right) $$
Penskalaan
Untuk mengubah ukuran suatu objek, transformasi penskalaan digunakan. Dalam proses penskalaan, Anda memperluas atau mengompresi dimensi objek. Penskalaan dapat dilakukan dengan mengalikan koordinat asli objek dengan faktor penskalaan untuk mendapatkan hasil yang diinginkan.
Mari kita asumsikan bahwa koordinat aslinya adalah (X, Y), faktor penskalaannya adalah (S X , S Y ), dan koordinat yang dihasilkan adalah (X ', Y'). Ini dapat direpresentasikan secara matematis seperti yang ditunjukkan di bawah ini -
X' = X . SX and Y' = Y . SY
Faktor skala S X , S Y menskalakan objek masing-masing dalam arah X dan Y. Persamaan di atas juga dapat direpresentasikan dalam bentuk matriks seperti di bawah ini -
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
ATAU
P’ = P . S
Dimana S adalah matriks skala. Proses penskalaan ditunjukkan pada gambar berikut.
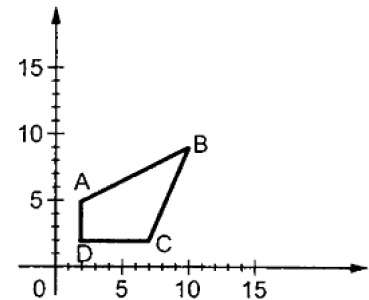
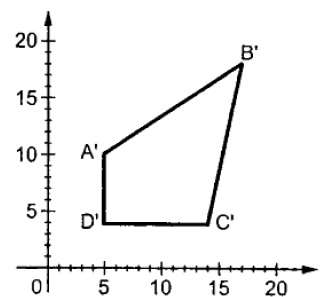
Jika kita memberikan nilai kurang dari 1 ke faktor penskalaan S, maka kita dapat mengurangi ukuran objek. Jika kita memberikan nilai lebih besar dari 1, maka kita bisa memperbesar ukuran benda tersebut.
Refleksi
Refleksi adalah bayangan cermin dari benda aslinya. Dengan kata lain, kita dapat mengatakan bahwa ini adalah operasi rotasi dengan 180 °. Dalam transformasi refleksi, ukuran objek tidak berubah.
Gambar berikut menunjukkan refleksi terhadap sumbu X dan Y, dan tentang asal masing-masing.
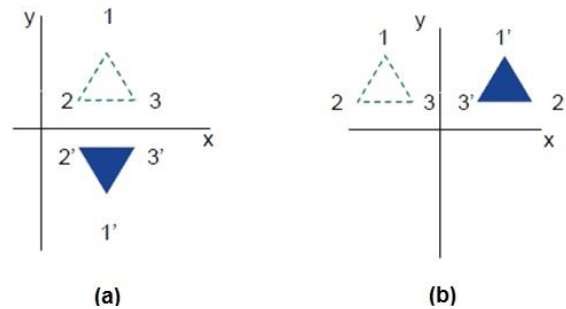
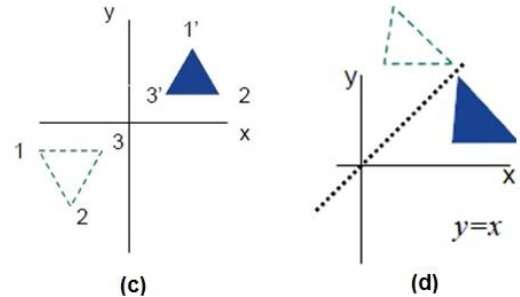
Mencukur
Transformasi yang memiringkan bentuk suatu objek disebut transformasi geser. Ada dua transformasi geserX-Shear dan Y-Shear. Satu menggeser nilai koordinat X dan menggeser nilai koordinat Y lainnya. Namun; dalam kedua kasus, hanya satu koordinat yang mengubah koordinatnya dan koordinat lainnya mempertahankan nilainya. Pemotongan juga disebut sebagaiSkewing.
X-Shear
X-Shear mempertahankan koordinat Y dan perubahan dilakukan pada koordinat X, yang menyebabkan garis vertikal miring ke kanan atau ke kiri seperti yang ditunjukkan pada gambar di bawah ini.
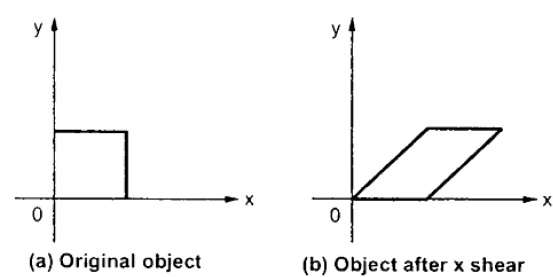
Matriks transformasi untuk X-Shear dapat direpresentasikan sebagai -
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y-Shear
Y-Shear mempertahankan koordinat X dan mengubah koordinat Y yang menyebabkan garis horizontal berubah menjadi garis miring ke atas atau ke bawah seperti yang ditunjukkan pada gambar berikut.
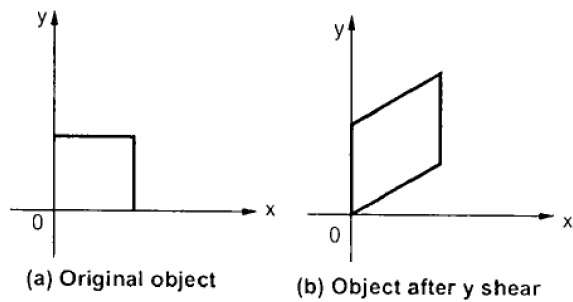
Y-Shear dapat direpresentasikan dalam matriks dari sebagai -
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ malu & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . Y
Y '= Y
Transformasi Komposit
Jika transformasi bidang T1 diikuti oleh transformasi bidang kedua T2, maka hasilnya sendiri dapat diwakili oleh transformasi tunggal T yang merupakan komposisi T1 dan T2 yang diambil dalam urutan tersebut. Ini ditulis sebagai T = T1 ∙ T2.
Transformasi komposit dapat dilakukan dengan penggabungan matriks transformasi untuk mendapatkan matriks transformasi gabungan.
Sebuah matriks gabungan -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
Di mana [Ti] adalah kombinasi dari
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
Perubahan urutan transformasi akan menimbulkan hasil yang berbeda, karena pada umumnya perkalian matriks tidak bersifat kumulatif yaitu [A]. [B] ≠ [B]. [A] dan urutan perkalian. Tujuan dasar penyusunan transformasi adalah untuk mendapatkan efisiensi dengan menerapkan satu transformasi tersusun ke satu titik, daripada menerapkan serangkaian transformasi, satu demi satu.
Misalnya, untuk memutar objek di sekitar titik sembarang (X p , Y p ), kita harus melakukan tiga langkah -
- Terjemahkan titik (X p , Y p ) ke asalnya.
- Putar tentang asalnya.
- Terakhir, terjemahkan pusat rotasi kembali ke tempatnya semula.