Grafik Komputer 3D
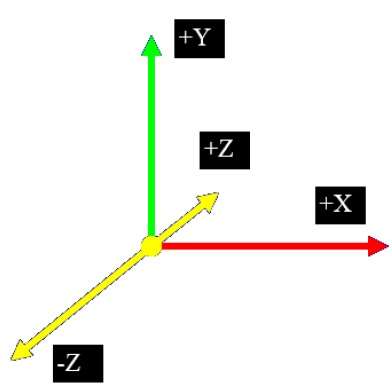
Dalam sistem 2D, kami hanya menggunakan dua koordinat X dan Y tetapi dalam 3D, koordinat tambahan Z ditambahkan. Teknik grafik 3D dan aplikasinya sangat penting untuk hiburan, permainan, dan industri desain dengan bantuan komputer. Ini adalah bidang penelitian berkelanjutan dalam visualisasi ilmiah.
Lebih jauh lagi, komponen grafik 3D sekarang menjadi bagian dari hampir setiap komputer pribadi dan, meskipun secara tradisional ditujukan untuk perangkat lunak intensif grafik seperti permainan, komponen tersebut semakin banyak digunakan oleh aplikasi lain.
Proyeksi Paralel
Proyeksi paralel membuang koordinat-z dan garis-garis sejajar dari setiap simpul pada objek diperpanjang hingga mereka memotong bidang pandang. Dalam proyeksi paralel, kami menentukan arah proyeksi, bukan pusat proyeksi.
Dalam proyeksi paralel, jarak dari pusat proyeksi ke bidang proyek tidak terbatas. Dalam jenis proyeksi ini, kami menghubungkan simpul yang diproyeksikan dengan segmen garis yang sesuai dengan koneksi pada objek asli.
Proyeksi paralel kurang realistis, tetapi bagus untuk pengukuran yang tepat. Dalam jenis proyeksi ini, garis sejajar tetap paralel dan sudut tidak dipertahankan. Berbagai jenis proyeksi paralel ditampilkan dalam hierarki berikut.
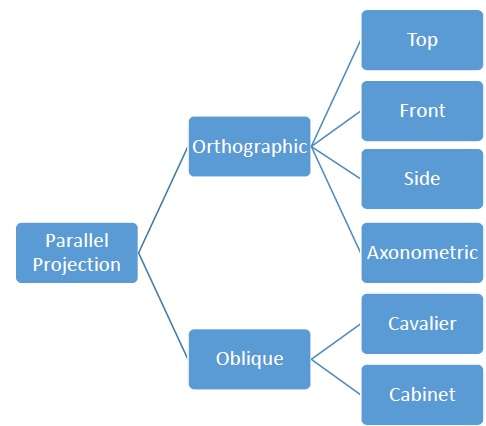
Proyeksi Ortografi
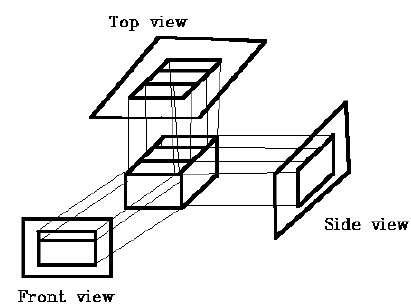
Dalam proyeksi ortografik arah proyeksi normal terhadap proyeksi bidang. Ada tiga jenis proyeksi ortografik -
- Proyeksi Depan
- Proyeksi Teratas
- Proyeksi Samping
Proyeksi Miring
Pada proyeksi miring, arah proyeksi tidak normal terhadap proyeksi bidang. Dalam proyeksi miring, kita dapat melihat objek lebih baik daripada proyeksi ortografik.
Ada dua jenis proyeksi miring - Cavalier dan Cabinet. Proyeksi Cavalier membuat sudut 45 ° dengan bidang proyeksi. Proyeksi garis tegak lurus terhadap bidang pandang memiliki panjang yang sama dengan garis itu sendiri pada proyeksi Cavalier. Dalam proyeksi yang lebih angkuh, faktor pemendek sebelumnya untuk ketiga arah utama adalah sama.
Proyeksi Kabinet membuat sudut 63,4 ° dengan bidang proyeksi. Dalam proyeksi Kabinet, garis tegak lurus ke permukaan tampilan diproyeksikan pada ½ panjang sebenarnya. Kedua proyeksi tersebut ditunjukkan pada gambar berikut -

Proyeksi Isometrik
Proyeksi ortografi yang menunjukkan lebih dari satu sisi objek disebut axonometric orthographic projections. Proyeksi aksonometri yang paling umum adalah anisometric projectiondi mana bidang proyeksi memotong setiap sumbu koordinat dalam sistem koordinat model pada jarak yang sama. Dalam proyeksi ini paralelisme garis dipertahankan tetapi sudut tidak dipertahankan. Gambar berikut menunjukkan proyeksi isometrik -

Proyeksi Perspektif
Dalam proyeksi perspektif, jarak dari pusat proyeksi ke bidang proyek terbatas dan ukuran benda bervariasi berbanding terbalik dengan jarak yang terlihat lebih realistis.
Jarak dan sudut tidak dipertahankan dan garis sejajar tidak tetap paralel. Sebaliknya, mereka semua bertemu pada satu titik yang disebutcenter of projection atau projection reference point. Ada 3 jenis proyeksi perspektif yang ditunjukkan pada bagan berikut.
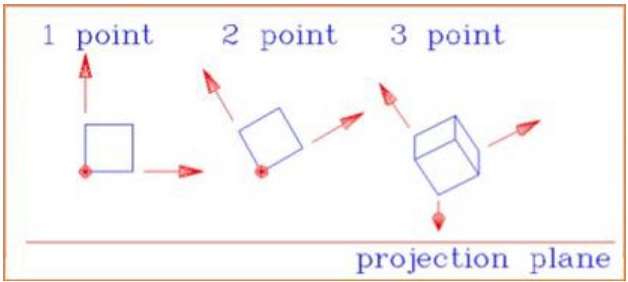
One point proyeksi perspektif sederhana untuk menggambar.
Two point proyeksi perspektif memberikan kesan kedalaman yang lebih baik.
Three point proyeksi perspektif paling sulit untuk digambar.
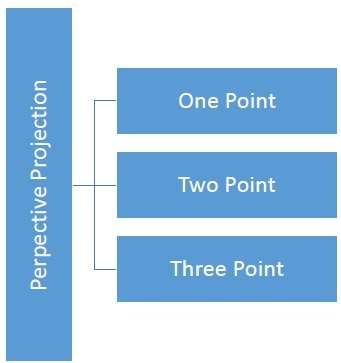
Gambar berikut menunjukkan ketiga jenis proyeksi perspektif -
Terjemahan
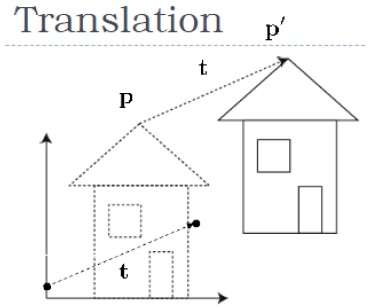
Dalam terjemahan 3D, kami mentransfer koordinat Z bersama dengan koordinat X dan Y. Proses penerjemahan dalam 3D mirip dengan terjemahan 2D. Terjemahan memindahkan objek ke posisi berbeda di layar.
Gambar berikut menunjukkan efek terjemahan -
Sebuah titik dapat diterjemahkan dalam 3D dengan menambahkan koordinat terjemahan $ (t_ {x,} t_ {y,} t_ {z}) $ ke koordinat asli (X, Y, Z) untuk mendapatkan koordinat baru (X ', Y ', Z').
$ T = \ mulai {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $
P '= P ∙ T
$ [X ′ \: \: Y ′ \: \: Z ′ \: \: 1] \: = \: [X \: \: Y \: \: Z \: \: 1] \: \ begin { bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $
$ = [X + t_ {x} \: \: \: Y + t_ {y} \: \: \: Z + t_ {z} \: \: \: 1] $