Algoritma Generasi Lingkaran
Menggambar lingkaran di layar agak rumit daripada menggambar garis. Ada dua algoritma populer untuk menghasilkan lingkaran -Bresenham’s Algorithm dan Midpoint Circle Algorithm. Algoritma ini didasarkan pada gagasan untuk menentukan titik-titik selanjutnya yang diperlukan untuk menggambar lingkaran. Mari kita bahas algoritma secara rinci -
Persamaan lingkarannya adalah $ X ^ {2} + Y ^ {2} = r ^ {2}, $ dengan r adalah jari-jari.
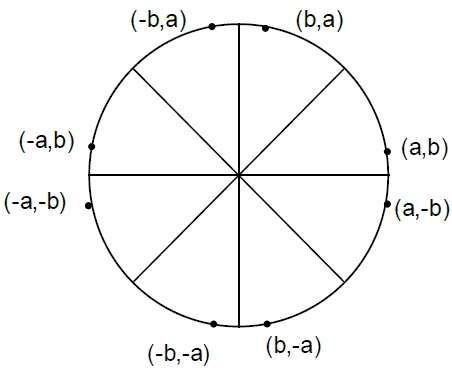
Algoritma Bresenham
Kami tidak dapat menampilkan busur berkelanjutan pada tampilan raster. Sebagai gantinya, kita harus memilih posisi piksel terdekat untuk menyelesaikan busur.
Dari ilustrasi berikut, Anda dapat melihat bahwa kita telah meletakkan piksel di lokasi (X, Y) dan sekarang perlu memutuskan di mana meletakkan piksel berikutnya - di N (X + 1, Y) atau di S (X + 1, Y-1).
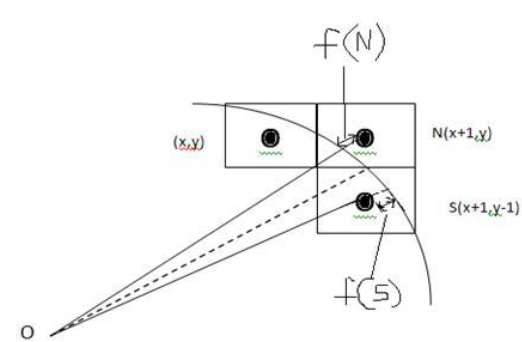
Ini dapat ditentukan oleh parameter keputusan d.
- Jika d <= 0, maka N (X + 1, Y) akan dipilih sebagai piksel berikutnya.
- Jika d> 0, maka S (X + 1, Y-1) akan dipilih sebagai piksel berikutnya.
Algoritma
Step 1- Dapatkan koordinat dari pusat lingkaran dan jari-jari, dan simpan masing-masing dalam x, y, dan R. Atur P = 0 dan Q = R.
Step 2 - Tetapkan parameter keputusan D = 3 - 2R.
Step 3 - Ulangi melalui langkah-8 saat P ≤ Q.
Step 4 - Panggil Draw Circle (X, Y, P, Q).
Step 5 - Tingkatkan nilai P.
Step 6 - Jika D <0 maka D = D + 4P + 6.
Step 7 - Set Lain R = R - 1, D = D + 4 (PQ) + 10.
Step 8 - Panggil Draw Circle (X, Y, P, Q).
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).Algoritma Titik Tengah
Step 1 - Radius masukan r dan pusatkan lingkaran $ (x_ {c,} y_ {c}) $ dan dapatkan titik pertama pada keliling lingkaran yang berpusat pada titik asal sebagai
(x0, y0) = (0, r)Step 2 - Hitung nilai awal parameter keputusan sebagai
$ P_ {0} $ = 5/4 - r (Lihat penjelasan berikut untuk penyederhanaan persamaan ini.)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0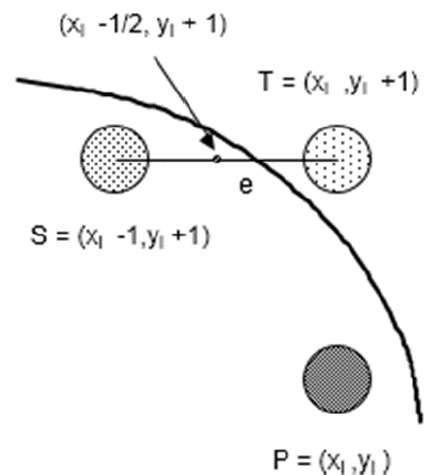
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 - Pada setiap posisi $ X_ {K} $ mulai dari K = 0, lakukan tes berikut -
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 - Tentukan titik simetri di tujuh oktan lainnya.
Step 5 - Pindahkan setiap menghitung posisi piksel (X, Y) ke jalur melingkar yang berpusat di $ (X_ {C,} Y_ {C}) $ dan plot nilai koordinat.
X = X + XC, Y = Y + YCStep 6 - Ulangi langkah-3 sampai 5 sampai X> = Y.