Permukaan Grafik Komputer

Permukaan Poligon

Objek direpresentasikan sebagai kumpulan permukaan. Representasi objek 3D dibagi menjadi dua kategori.

Boundary Representations (B-reps) - Ini menggambarkan objek 3D sebagai satu set permukaan yang memisahkan interior objek dari lingkungan.
Space–partitioning representations - Ini digunakan untuk mendeskripsikan properti interior, dengan mempartisi wilayah spasial yang berisi objek menjadi sekumpulan padatan kecil, tidak tumpang tindih, dan berdekatan (biasanya kubus).

Representasi batas yang paling umum digunakan untuk objek grafik 3D adalah sekumpulan poligon permukaan yang membungkus interior objek. Banyak sistem grafis menggunakan metode ini. Kumpulan poligon disimpan untuk deskripsi objek. Ini menyederhanakan dan mempercepat rendering permukaan dan tampilan objek karena semua permukaan dapat dijelaskan dengan persamaan linier.

Permukaan poligon umum digunakan dalam desain dan aplikasi pemodelan padat, sejak itu wireframe displaydapat dilakukan dengan cepat untuk memberikan indikasi umum struktur permukaan. Kemudian pemandangan realistis dihasilkan dengan menginterpolasi pola bayangan di seluruh permukaan poligon untuk menerangi.

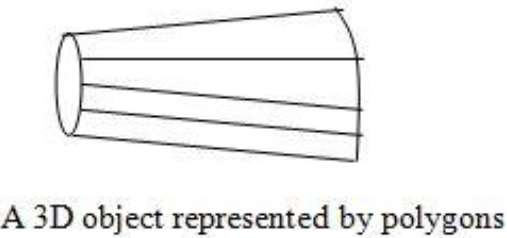
Tabel Poligon

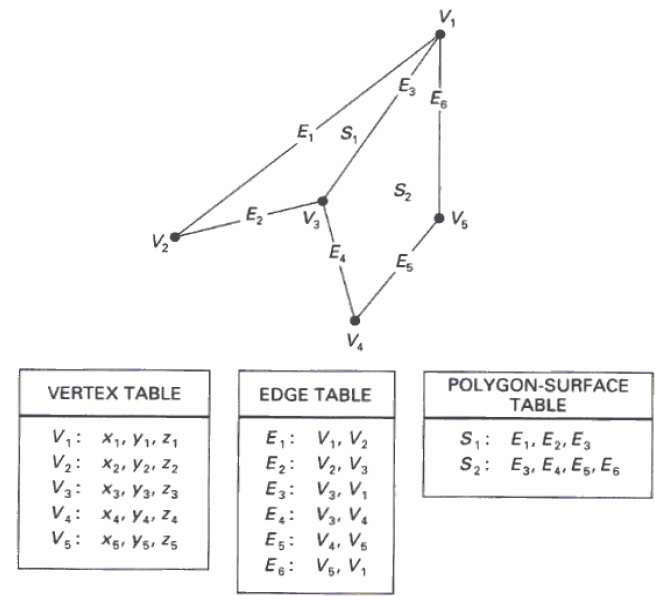
Dalam metode ini, permukaan ditentukan oleh himpunan koordinat puncak dan atribut terkait. Seperti yang ditunjukkan pada gambar berikut, ada lima simpul, dari v ₁ sampai v ₅ .

Setiap simpul menyimpan informasi koordinat x, y, dan z yang direpresentasikan dalam tabel sebagai v ₁ : x ₁ , y ₁ , z ₁ .
Tabel Edge digunakan untuk menyimpan informasi edge dari poligon. Pada gambar berikut, sisi E ₁ terletak di antara simpul v ₁ dan v ₂ yang direpresentasikan dalam tabel sebagai E ₁ : v ₁ , v ₂ .
Tabel permukaan poligon menyimpan jumlah permukaan yang ada dalam poligon. Dari gambar berikut, permukaan S ₁ ditutupi oleh tepi E ₁ , E ₂ dan E ₃ yang dapat direpresentasikan dalam tabel permukaan poligon sebagai S ₁ : E ₁ , E ₂ , dan E ₃ .

Persamaan Bidang

Persamaan permukaan bidang dapat dinyatakan sebagai -

Ax + Oleh + Cz + D = 0

Di mana (x, y, z) adalah sembarang titik pada bidang, dan koefisien A, B, C, dan D adalah konstanta yang menjelaskan sifat spasial bidang tersebut. Kita dapat memperoleh nilai A, B, C, dan D dengan menyelesaikan sekumpulan persamaan bidang menggunakan nilai koordinat untuk tiga titik bukan collinear pada bidang tersebut. Mari kita asumsikan bahwa tiga simpul bidang adalah (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) dan (x ₃ , y ₃ , z ₃ ).

Mari kita selesaikan persamaan simultan berikut untuk rasio A / D, B / D, dan C / D. Anda mendapatkan nilai A, B, C, dan D.

(A / D) x ₁ + (B / D) y ₁ + (C / D) z ₁ = -1

(A / D) x ₂ + (B / D) y ₂ + (C / D) z ₂ = -1

(A / D) x ₃ + (B / D) y ₃ + (C / D) z ₃ = -1

Untuk mendapatkan persamaan di atas dalam bentuk determinan, terapkan aturan Cramer pada persamaan di atas.

$ A = \ mulai {bmatrix} 1 & y_ {1} & z_ {1} \\ 1 & y_ {2} & z_ {2} \\ 1 & y_ {3} & z_ {3} \ end {bmatrix} B = \ mulai {bmatrix} x_ {1} & 1 & z_ {1} \\ x_ {2} & 1 & z_ {2} \\ x_ {3} & 1 & z_ {3} \ end {bmatrix} C = \ begin {bmatrix} x_ {1} & y_ {1} & 1 \\ x_ {2} & y_ {2} & 1 \\ x_ {3} & y_ {3} & 1 \ end {bmatrix} D = - \ begin {bmatrix} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \ end {bmatrix } $

Untuk setiap titik (x, y, z) dengan parameter A, B, C, dan D, kita dapat mengatakan bahwa -

Ax + By + Cz + D ≠ 0 artinya titik tersebut bukan pada bidang.
Ax + By + Cz + D <0 artinya titik tersebut ada di dalam permukaan.
Ax + By + Cz + D> 0 artinya titik berada di luar permukaan.

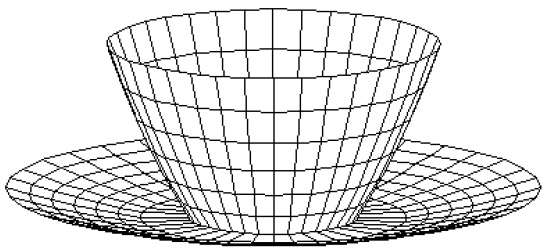
Jala Poligon

Permukaan dan padatan 3D dapat diperkirakan dengan satu set elemen poligonal dan garis. Permukaan seperti itu disebutpolygonal meshes. Dalam jaring poligon, setiap tepi dibagi oleh paling banyak dua poligon. Kumpulan poligon atau wajah, bersama-sama membentuk "kulit" objek.

Metode ini dapat digunakan untuk merepresentasikan kelas luas dari padatan / permukaan dalam grafik. Jaring poligonal dapat dirender menggunakan algoritma penghilangan permukaan tersembunyi. Jaring poligon dapat diwakili dengan tiga cara -