Algoritma Pengisian Poligon
Poligon adalah daftar simpul yang diurutkan seperti yang ditunjukkan pada gambar berikut. Untuk mengisi poligon dengan warna tertentu, Anda perlu menentukan piksel yang berada di tepi poligon dan yang berada di dalam poligon. Dalam bab ini, kita akan melihat bagaimana kita dapat mengisi poligon dengan menggunakan teknik yang berbeda.

Pindai Algoritma Garis
Algoritma ini bekerja dengan memotong garis pindai dengan tepi poligon dan mengisi poligon di antara pasangan persimpangan. Langkah-langkah berikut menggambarkan cara kerja algoritma ini.
Step 1 - Cari tahu Ymin dan Ymax dari poligon yang diberikan.
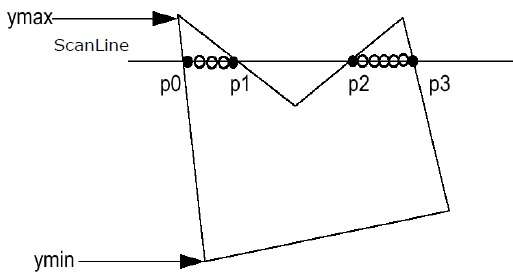
Step 2- ScanLine berpotongan dengan setiap tepi poligon dari Ymin ke Ymax. Beri nama setiap titik potong poligon. Sesuai gambar yang ditunjukkan di atas, mereka dinamai sebagai p0, p1, p2, p3.
Step 3 - Urutkan titik potong dalam urutan koordinat X yang semakin meningkat yaitu (p0, p1), (p1, p2), dan (p2, p3).
Step 4 - Isi semua pasangan koordinat yang ada di dalam poligon dan abaikan pasangan alternatifnya.
Algoritma Pengisian Banjir
Terkadang kita menemukan objek yang ingin kita isi area dan batasnya dengan warna yang berbeda. Kita bisa melukis objek seperti itu dengan warna interior tertentu daripada mencari warna batas tertentu seperti pada algoritma pengisian batas.
Alih-alih bergantung pada batas objek, itu bergantung pada warna isian. Dengan kata lain, ini menggantikan warna interior objek dengan warna isian. Jika tidak ada lagi piksel dari warna interior asli, algoritme selesai.
Sekali lagi, algoritma ini mengandalkan metode Four-connect atau Eight-connect untuk mengisi piksel. Tetapi alih-alih mencari warna batas, ia mencari semua piksel yang berdekatan yang merupakan bagian dari interior.
Algoritma Pengisian Batas
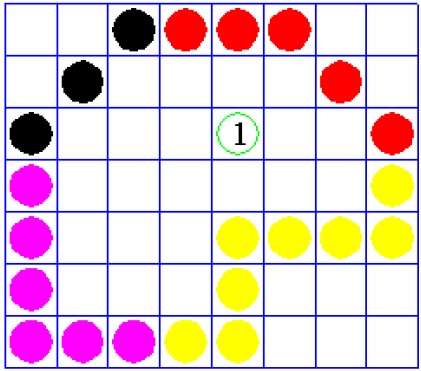
Algoritme pengisian batas berfungsi sesuai namanya. Algoritma ini mengambil satu titik di dalam sebuah objek dan mulai mengisi hingga mencapai batas objek tersebut. Warna batas dan warna yang kita isi harus berbeda agar algoritme ini berfungsi.
Dalam algoritma ini, kami mengasumsikan bahwa warna batasnya sama untuk keseluruhan objek. Algoritme pengisian batas dapat diimplementasikan dengan 4 piksel yang terhubung atau 8 piksel yang terhubung.
Poligon 4-Terhubung
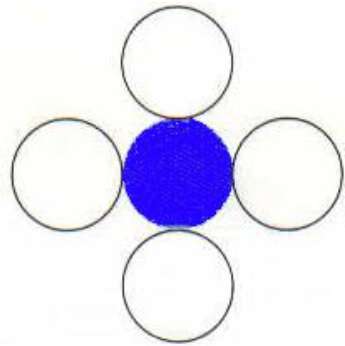
Dalam teknik ini 4 piksel yang terhubung digunakan seperti yang ditunjukkan pada gambar. Kami meletakkan piksel di atas, di bawah, ke kanan, dan ke sisi kiri piksel saat ini dan proses ini akan berlanjut hingga kami menemukan batas dengan warna berbeda.
Algoritma
Step 1 - Inisialisasi nilai seed point (seedx, seedy), fcolor dan dcol.
Step 2 - Tentukan nilai batas poligon.
Step 3 - Periksa apakah titik benih saat ini adalah warna default, kemudian ulangi langkah 4 dan 5 hingga piksel batas tercapai.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - Ubah warna default dengan warna isian pada titik benih.
setPixel(seedx, seedy, fcol)Step 5 - Ikuti prosedur secara rekursif dengan empat titik lingkungan.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - Keluar
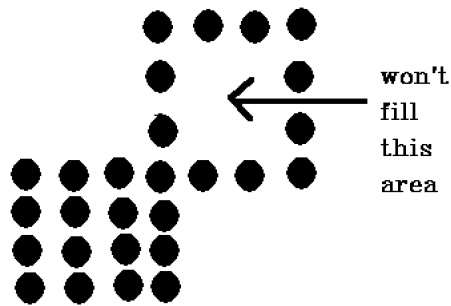
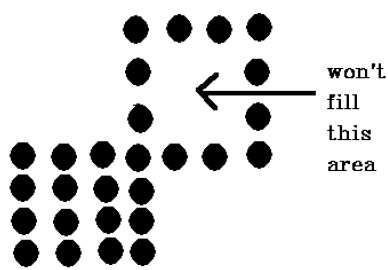
Ada masalah dengan teknik ini. Pertimbangkan kasus seperti yang ditunjukkan di bawah ini di mana kami mencoba mengisi seluruh wilayah. Di sini, gambar hanya diisi sebagian. Dalam kasus seperti itu, teknik 4 piksel yang terhubung tidak dapat digunakan.
Poligon 8-Terhubung
Dalam teknik ini digunakan 8 piksel yang terhubung seperti yang ditunjukkan pada gambar. Kami menempatkan piksel di atas, di bawah, kanan dan kiri piksel saat ini seperti yang kami lakukan dalam teknik 4-terhubung.
Selain itu, kami juga menempatkan piksel dalam diagonal sehingga seluruh area piksel saat ini tertutup. Proses ini akan berlanjut hingga kita menemukan batas dengan warna berbeda.

Algoritma
Step 1 - Inisialisasi nilai seed point (seedx, seedy), fcolor dan dcol.
Step 2 - Tentukan nilai batas poligon.
Step 3 - Periksa apakah titik benih saat ini adalah warna default kemudian ulangi langkah 4 dan 5 hingga piksel batas tercapai
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - Ubah warna default dengan warna isian pada titik benih.
setPixel(seedx, seedy, fcol)Step 5 - Ikuti prosedur secara rekursif dengan empat titik lingkungan
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - Keluar
Teknik 4 piksel terkoneksi gagal mengisi area seperti yang ditandai pada gambar berikut yang tidak akan terjadi pada teknik 8 terkoneksi.
Tes di dalam-luar
Metode ini juga dikenal sebagai counting number method. Saat mengisi suatu objek, kita sering kali perlu mengidentifikasi apakah titik tertentu ada di dalam objek atau di luarnya. Ada dua metode yang dapat kita gunakan untuk mengidentifikasi apakah titik tertentu ada di dalam suatu objek atau di luar.
- Aturan Ganjil-Genap
- Aturan nomor belitan bukan nol
Aturan Ganjil-Genap
Dalam teknik ini, kita akan menghitung tepi yang melintasi garis dari titik mana pun (x, y) hingga tak terhingga. Jika jumlah interaksi ganjil, maka titik (x, y) adalah titik interior; dan jika jumlah interaksinya genap, maka titik (x, y) adalah titik eksterior. Contoh berikut menggambarkan konsep ini.
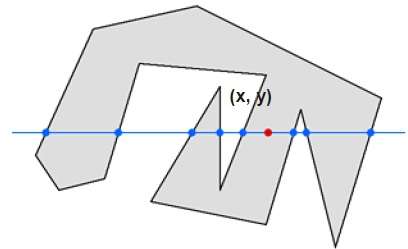
Dari gambar di atas, kita dapat melihat bahwa dari titik (x, y), banyaknya titik interaksi di sisi kiri adalah 5 dan di sisi kanan adalah 3. Dari kedua ujungnya, jumlah titik interaksi adalah ganjil, jadi intinya dipertimbangkan di dalam objek.
Aturan Nomor Berliku Bukan Nol
Metode ini juga digunakan dengan poligon sederhana untuk menguji titik yang diberikan interior atau tidak. Ini dapat dipahami secara sederhana dengan bantuan pin dan karet gelang. Pasang pin di salah satu tepi poligon dan ikat karet gelang di dalamnya lalu regangkan karet gelang di sepanjang tepi poligon.
Ketika semua tepi poligon tertutup oleh karet gelang, periksa pin yang telah dipasang di titik yang akan diuji. Jika kita menemukan setidaknya satu angin pada titik tersebut, pertimbangkan itu dalam poligon, jika tidak, kita dapat mengatakan bahwa titik tersebut tidak berada di dalam poligon.
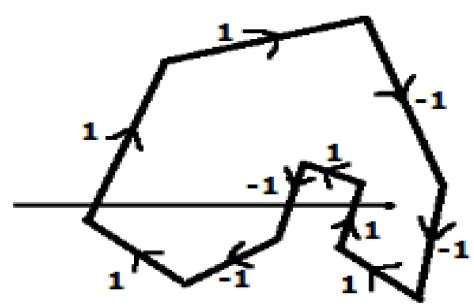
Dalam metode alternatif lain, berikan arah ke semua tepi poligon. Gambar garis pindai dari titik yang akan diuji ke arah paling kiri dari arah X.
Berikan nilai 1 ke semua sisi yang mengarah ke atas dan -1 lainnya sebagai nilai arah.
Periksa nilai arah tepi yang dilewati garis pindai dan jumlahkan.
Jika jumlah total nilai arah ini bukan nol, maka titik yang akan diuji ini adalah interior point, jika tidak, itu adalah exterior point.
Pada gambar di atas, kami menjumlahkan nilai arah dari mana garis pindai melewati maka totalnya adalah 1 - 1 + 1 = 1; yang bukan nol. Jadi intinya dikatakan sebagai titik interior.