Penalaran - Kubus dan Kubus
Saat ini, pertanyaan berdasarkan 'Cubes and Cuboids' ditanyakan di hampir setiap ujian kompetitif. Masalah ini sangat sering terjadi dalam berbagai ujian kompetitif.
Metode yang dijelaskan di bawah ini sederhana namun elegan. Mereka harus sangat mudah dimengerti dan dengan sedikit latihan Anda harus menguasainya. Kubus adalah benda padat tiga dimensi yang memiliki 6 sisi, 12 sisi, dan sudut. Semua tepi kubus sama dan semua permukaannya berbentuk persegi. Itu adalah sosok padat yang memiliki 6 wajah; setiap wajah disebut persegia cube. Jika masing-masing dari enam sisi berbentuk persegi panjang, disebutcuboid. Kubus juga disebut arectangular parallelepiped.
Pertanyaan yang diajukan pada kubus dan kubus mungkin dari jenis berikut.
Ketik I
Beberapa tampilan kubus lengkap diberikan dan Anda harus menemukan bagian mana dari kubus yang terletak tepat di bawah bagian tertentu.
Tipe II
Kubus terbuka diberikan dan Anda harus memprediksi seperti apa bentuknya ketika ditutup menjadi kubus.
Tipe III
Sebuah kubus tidak dapat dipernis pada atau sebagian mukanya dengan warna yang sama atau warna yang berbeda dan kemudian dipotong menjadi potongan-potongan identik dalam jumlah tertentu. Lalu pertanyaan bentuk- "berapa banyak kubus kecil yang 2 wajah dipernis?" Berapa banyak kubus kecil yang hanya memiliki satu wajah yang dipernis? dll.
Ada dua jenis soal yang muncul dalam ujian. Pada awalnya, Anda diberikan beberapa tampilan dari acomplete cube, dan Anda harus menyatakan bagian kubus mana yang terletak persis di bawah bagian tertentu. Di tipe lain, Anda diberiopened-up cube, dan Anda harus memprediksi seperti apa tampilannya ketika ditutup menjadi kubus.
For Example -
Beberapa permukaan kubus ditunjukkan di bawah ini -

Angka mana yang berlawanan dengan 2?
A - 1
B - 6
C - 5
D - 4
Pendekatan fundamentalnya adalah sebagai berikut -
Ketik I
A fundamental rule: Opposite cannot be together;
Kapanpun kita melihat sebuah kubus, dengan hanya tiga wajahnya yang terlihat oleh kita, kita tidak pernah bisa melihat dua wajah yang berlawanan secara bersamaan. Dengan semua aturan ini, kita dapat dengan mudah menyelesaikan jenis masalah yang dibahas di atas. Dalam pertanyaan di atas di mana kita harus menemukan wajah yang berlawanan dari wajah tertentu, kita dapat menghilangkan wajah yang muncul bersama-sama dengan X dalam tampilan apa pun. Dengan demikian, kami dapat menghilangkan semua pilihan lain dan sisanya akan menjadi jawaban kami.
Pada titik ini, Anda harus membaca paragraf sebelumnya sekali lagi dan melihat bahwa Anda memahami konsepnya. Setelah ini, Anda harus mencoba memecahkan contoh di atas dan melihat apakah Anda dapat menerapkan konsep yang dibahas di atas. Namun, Anda menemukan bahwa Anda belum memahami konsepnya sepenuhnya, tidak masalah. Lanjutkan membaca bagian ini. Segalanya akan menjadi jelas setelah Anda menyelesaikan bagian tersebut. Dengan aturan fundamental sebelumnya di belakang pikiran Anda, Anda dapat memecahkan jenis pertanyaan di atas.
Untuk pertanyaannya, aturannya sendiri sudah cukup. Setelah itu, Anda bisa menyelesaikannya lebih cepat denganthree secondary rules.
Solution for above example -
Dalam contoh yang diberikan, kita harus mencari wajah yang berlawanan 2. Sekarang pada gambar pertama, 2 muncul bersama dengan 1 dan 3. Artinya baik 1 maupun 3 tidak bisa berlawanan dengan 2. Itu berarti kebalikan dari 1 kita bisa memiliki 4 atau 5 atau 6. Demikian pula, berlawanan dengan 3 kita dapat memiliki 4 atau 5 atau 6. Sekarang, lihat gambar kedua. Di sini, 3 dan 1 muncul bersama-sama dengan 5. Ini berarti bahwa 5 berlawanan dengan bukan 3 atau 1. Jadi, itu berarti bahwa 4 atau 6 berlawanan dengan 1 dan yang lainnya berlawanan dengan 3 jadi 5 harus berlawanan 2. Oleh karena itu 5 benar menjawab.
Beberapa Aturan Lebih Cepat
Sekarang Anda pasti sudah memahami trik dasar untuk menyelesaikan pertanyaan semacam itu. Triknya adalah Anda harus menghilangkan pilihan-pilihan yang tidak mungkin dilakukan. Untuk ini, Anda mengambil bantuan dari aturan dasar yang mengatakan bahwa jika dua sisi berlawanan satu sama lain, kemunculannya secara bersamaan dalam satu tampilan kubus tidak dimungkinkan. Namun, dalam kompetisi yang sangat berharga saat ini, konsep saja tidak akan berhasil. Anda harus bisa menyelesaikan pertanyaan dengan cepat. Ada beberapa aturan sekunder untuk menyelesaikan pertanyaan.
Rule I- Mari kita sebut angka itu X, kebalikan dari yang harus Anda temukan. Misalkan dalam salah satu tampilan kubus, X muncul dengan Y dan Z. Bersama dengan angka ketiga (katakanlah A), maka X akan berlawanan dengan A.
Jadi sebagai contoh, Anda harus mencari wajah yang berlawanan 2. (Ini adalah X kami). Sekarang, 2 muncul dalam satu gambar bersama dengan 1 dan 3. (Y dan Z). Juga 1 dan 3 muncul bersama dalam satu gambar lagi, bersama dengan 5. (Yaitu A). Karenanya 2 harus berlawanan 5.
Rule II- Kita harus menemukan wajah berlawanan dari 'X'. Misalkan dalam satu tampilan kubus, X muncul dengan Y dan Z. Sekarang, anggaplah Y dan Z tidak muncul bersama dalam tampilan lain, tetapi mereka muncul secara terpisah dalam dua atau lebih tampilan berbeda. Kemudian angka umum antara dua tampilan lagi di mana Y dan Z muncul secara terpisah, akan menjadi angka di seberang X.
Rule III- Sebut saja angka X, kebalikan dari yang harus Anda temukan. Sekarang, misalkan X muncul dalam dua tampilan dan dalam dua tampilan ini empat sosok berbeda terlihat dengan X. Maka satu-satunya sosok yang tidak terlihat dengan X dalam dua tampilan ini harus berlawanan dengan X.
Summary- Anda harus menyimpan aturan fundamental di belakang pikiran Anda dan kemudian menerapkan tiga aturan sekunder untuk jawaban cepat. Keseluruhan pendekatan dapat diringkas dengan diagram berikut.
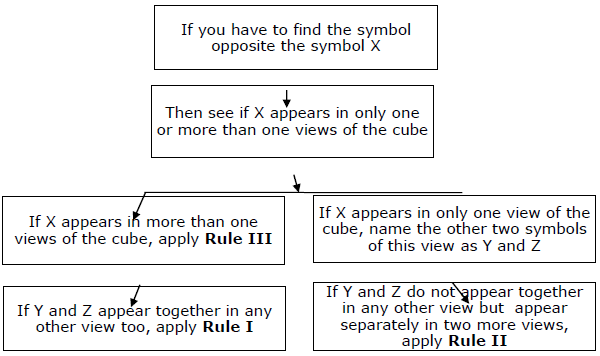
Tipe II
Dalam tipe ini, kami menggunakan aturan fundamental. Aturan ini membantu kami menghilangkan kombinasi tersebut di mana wajah berlawanan ditampilkan dalam satu tampilan. Jadi itu akan mengarah pada penghapusan pilihan asalkan kita tahu bagaimana menentukan wajah mana yang akan berlawanan satu sama lain, dengan melihat "opened-up cube". Untuk tujuan ini, ada aturan yang sangat sederhana yang dapat Anda gunakan dengan melihatopened-up cube, yang mana wajah akan berseberangan hanya dengan melihatnya.
Aturan diberikan di bawah ini;
Third is opposite rule -
Jika Anda ingin mengetahui wajah kebalikan dari sebuah wajah (katakanlah X), pada gambar I, II, III; kubus terbuka diberikan. Kami harus menemukan wajah mana yang berlawanan satu sama lain saat kubus ditutup.
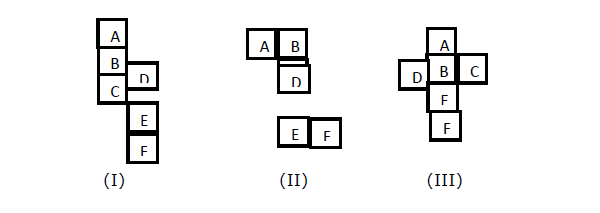
Explanation -
Dalam gambar (I), angka ketiga ke A adalah C. Jadi A kebalikan dari C. Jadi, D dan F akan berlawanan. B dan E akan berlawanan.
Pada gambar (II), B adalah ketiga dari D, jadi B akan berlawanan dengan D. Demikian pula, C akan berlawanan dengan E dan A akan berlawanan dengan F.
Pada gambar (III), A berlawanan dengan E, B berlawanan dengan F. Oleh karena itu, C berlawanan dengan D.
Steps to solve problem
Sekarang kita dapat memecahkan pertanyaan jenis ini. Kita tahu bagaimana menemukan wajah yang berlawanan dengan melihatOpened-up cube. Kita juga tahu bahwa dalam tampilan kubus mana pun, permukaan yang berlawanan tidak dapat bersatu. Oleh karena itu, menggabungkan dua aturan, kita dapat dengan mudah menyelesaikan masalah.
Ringkasan
Dengan ini, diskusi tentang bagaimana menyelesaikan pertanyaan tipe II selesai. Anda harus menggunakan aturan ketiga untuk menentukan wajah mana yang berlawanan satu sama lain. Diagram berikut akan memberikan informasi lengkap tentang pendekatan ini.

Tipe III
Counting of Cubes (when a varnished solid cube is cut);
Pada bagian sebelumnya, kita telah membahas masalah menemukan sisi berlawanan dari kubus. Ada jenis pertanyaan lain yang berkaitan dengan kubus di mana kubus yang lebih besar dengan warna berbeda dipernis pada sisi yang berbeda, dipecah menjadi beberapa kubus yang lebih kecil dan Anda harus menemukan jumlah kubus yang hanya satu sisi dipernis atau dua sisi dipernis.
Format of this problem -
Example -
Sebuah kubus dipernis dengan tiga warna hijau, biru dan merah pada sisinya, dengan setiap warna dipernis pada dua sisi berlawanan dari kubus. Sekarang kubus tersebut dipecah menjadi 64 kubus dengan ukuran yang sama. Berdasarkan informasi ini, jawablah pertanyaan berikut -
1. Berapa banyak kubus yang dua sisinya dipernis dan sisinya tidak dipernis?
A - 18
B - 20
C - 22
D - 24
2. Berapa kubus yang hanya memiliki satu sisi yang dipernis (dengan warna hijau atau biru saja)
A - 4
B - 24
C - 16
D - 12
3. Berapa banyak kubus yang sisinya tidak dipernis?
A - 0
B - 8
C - 12
D - 64