Penalaran - Pengurangan Logis
Pengurangan logis merupakan bab penting karena banyak pertanyaan mudah dan menarik dari bab ini disertakan dalam berbagai ujian kompetitif. Dalam bab ini, kita akan membahas dua metode untuk menyelesaikan masalah tersebut -
- Metode silogisme
- Metode diagram Venn
Dasar
Jika ada dua pernyataan, maka silogisme akan menjadi cara terbaik untuk menyelesaikan masalah tetapi jika jumlah pernyataan lebih dari dua, maka gunakan metode diagram Venn. Terkadang pernyataan dan kesimpulan berasal dari fakta yang diterima secara umum tetapi bisa juga tidak logis. Misalnya -
a) Beberapa kursi adalah pintu.
b) Semua pria adalah wanita
c) Tidak ada susu yang berwarna putih
Untuk sampai pada kesimpulan tersebut diperlukan pemikiran abstrak. Seseorang perlu memahami pengertian logis dari kalimat tersebut kemudian harus menjawab kesimpulan yang sesuai. Setiap pernyataan perlu dianggap benar maka kita harus memverifikasi apakah kesimpulan secara logis mengikuti pernyataan tersebut.
Kualifikasi
Ini adalah beberapa kata dasar yang digunakan untuk menggambarkan seberapa mirip atau berbeda suatu hal dengan yang lain. Contoh dari beberapa kualifikasi adalah "Semua", "Beberapa", "Beberapa-tidak" dll.
Konsep diagram Venn
Di sisi lain, diagram Venn adalah proses dimana kita dapat merepresentasikan sebuah kalimat atau pernyataan dalam bentuk figur geometris. Semua pernyataan yang diberikan diplot dalam kemungkinan diagram Venn. Kemudian semua kesimpulan diverifikasi dengan diagram tersebut. Setiap kesimpulan yang memenuhi semua diagram Venn akan dianggap sebagai kesimpulan yang valid.
| Pernyataan | Diagram Venn yang Sesuai |
|---|---|
| Semua A adalah B |
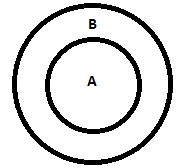
|
| Beberapa A adalah B (OR) Beberapa A bukan B |
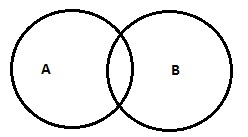
|
| Tidak A adalah B |
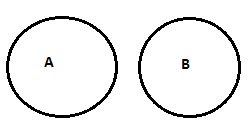
|
Mari kita ambil contoh sederhana untuk memahaminya dengan cara yang lebih baik.
Sample − 1
Statements -
Semua insinyur itu bodoh. Semua orang bodoh adalah dokter. Semua dokter miskin.
Conclusions -
I. Beberapa orang miskin adalah orang bodoh.
II. Beberapa orang miskin adalah insinyur.
Options -
A - Hanya aku yang valid
B - Hanya II yang valid
C - Kedua pernyataan itu valid
D - Tidak ada pernyataan yang valid
Answer - Opsi C
Explanation -
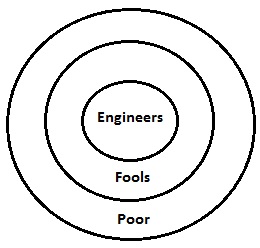
Diagram Venn untuk pernyataan yang diberikan digambar di atas. Ini menunjukkan semua pernyataan dalam diagram di satu tempat. Di sini sekarang jika kita akan membahas tentang kesimpulan satu per satu, semuanya akan jelas.
Di sini orang bodoh adalah bagian dari orang miskin. Jadi adalah fakta yang jelas bahwa beberapa orang miskin akan menjadi bodoh. Oleh karena itu, kesimpulan I valid. Demikian pula, kesimpulan II valid karena insinyur juga merupakan bagian dari orang miskin. Oleh karena itu, kedua pernyataan tersebut akan valid.
Sample − 2
Statements -
Beberapa keyboard adalah Mouse. Beberapa Mouse adalah radio.
Conclusions -
I. Beberapa keyboard adalah radio.
II. Beberapa radio adalah keyboard
AKU AKU AKU. Semua radio adalah Mouse.
IV. Semua Mouse adalah keyboard.
Options -
A - Hanya kesimpulan I yang valid
B - Hanya kesimpulan II yang valid
C - Baik I atau II valid
D - Tidak ada kesimpulan yang valid
E - Baik I dan II valid
Answer - Opsi D
Explanation - Karena kedua pernyataan itu khusus, tidak ada kesimpulan pasti yang valid.
Sample − 3
Statements -
Semua siswa tidak mabuk. Semua siswa nakal.
Conclusions -
I. Semua anak nakal tidak mabuk atau sebaliknya.
II. Beberapa orang yang tidak mabuk memang nakal.
AKU AKU AKU. Biasanya nakal adalah orang yang sadar.
IV. Kejahatan dan rasa bersalah berjalan seiring.
Options -
A - Hanya kesimpulan I yang valid
B - Hanya kesimpulan II yang valid
C - Baik I atau II valid
D - Tidak ada I atau II yang valid
E - Baik I dan II valid
Answer - Opsi B
Explanation- Karena istilah menengah 'siswa' didistribusikan dua kali dalam pernyataan, kesimpulannya tidak boleh luas. Jadi, sah bahwa 'Beberapa orang yang sadar itu nakal'. Jadi, II benar.