アソシエイトメモリネットワーク
これらの種類のニューラルネットワークは、パターンの関連付けに基づいて機能します。つまり、さまざまなパターンを保存でき、出力を提供するときに、指定された入力パターンと照合することで、保存されたパターンの1つを生成できます。これらのタイプの記憶は、Content-Addressable Memory(カム)。連想メモリは、格納されているパターンをデータファイルとして並列検索します。
以下は私たちが観察できる2つのタイプの連想記憶です-
- 自動連想メモリ
- ヘテロ連想記憶
自動連想メモリ
これは、入力トレーニングベクトルと出力ターゲットベクトルが同じである単層ニューラルネットワークです。重みは、ネットワークが一連のパターンを格納するように決定されます。
建築
次の図に示すように、自動連想メモリネットワークのアーキテクチャには ‘n’ 入力トレーニングベクトルの数など ‘n’ 出力ターゲットベクトルの数。
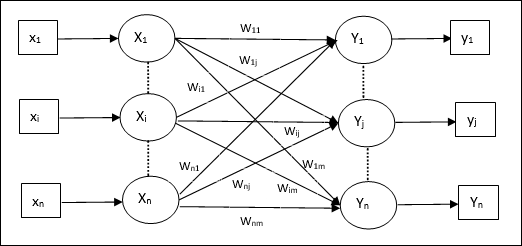
トレーニングアルゴリズム
トレーニングでは、このネットワークはヘッブまたはデルタの学習ルールを使用しています。
Step 1 −すべての重みをゼロに初期化します。 wij = 0 (i = 1 to n, j = 1 to n)
Step 2 −入力ベクトルごとに手順3〜4を実行します。
Step 3 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 4 −各出力ユニットを次のようにアクティブにします−
$$ y_ {j} \:= \:s_ {j} \ :( j \:= \:1 \:to \:n)$$
Step 5 −次のように重みを調整します−
$$ w_ {ij}(new)\:= \:w_ {ij}(old)\:+ \:x_ {i} y_ {j} $$
テストアルゴリズム
Step 1 −ヘッブの法則のトレーニング中に取得した重みを設定します。
Step 2 −入力ベクトルごとに手順3〜5を実行します。
Step 3 −入力ユニットのアクティブ化を入力ベクトルのアクティブ化と同じに設定します。
Step 4 −各出力ユニットへの正味入力を計算します j = 1 to n
$$ y_ {inj} \:= \:\ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 −次の活性化関数を適用して出力を計算します
$$ y_ {j} \:= \:f(y_ {inj})\:= \:\ begin {cases} + 1&if \:y_ {inj} \:> \:0 \\-1&if \:y_ {inj} \:\ leqslant \:0 \ end {cases} $$
ヘテロ連想記憶
自動連想メモリネットワークと同様に、これも単層ニューラルネットワークです。ただし、このネットワークでは、入力トレーニングベクトルと出力ターゲットベクトルは同じではありません。重みは、ネットワークが一連のパターンを格納するように決定されます。ヘテロ連想ネットワークは本質的に静的であるため、非線形および遅延操作はありません。
建築
次の図に示すように、Hetero AssociativeMemoryネットワークのアーキテクチャには ‘n’ 入力トレーニングベクトルの数と ‘m’ 出力ターゲットベクトルの数。
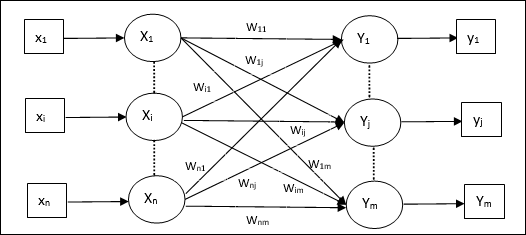
トレーニングアルゴリズム
トレーニングでは、このネットワークはヘッブまたはデルタの学習ルールを使用しています。
Step 1 −すべての重みをゼロに初期化します。 wij = 0 (i = 1 to n, j = 1 to m)
Step 2 −入力ベクトルごとに手順3〜4を実行します。
Step 3 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 4 −各出力ユニットを次のようにアクティブにします−
$$ y_ {j} \:= \:s_ {j} \ :( j \:= \:1 \:to \:m)$$
Step 5 −次のように重みを調整します−
$$ w_ {ij}(new)\:= \:w_ {ij}(old)\:+ \:x_ {i} y_ {j} $$
テストアルゴリズム
Step 1 −ヘッブの法則のトレーニング中に取得した重みを設定します。
Step 2 −入力ベクトルごとに手順3〜5を実行します。
Step 3 −入力ユニットのアクティブ化を入力ベクトルのアクティブ化と同じに設定します。
Step 4 −各出力ユニットへの正味入力を計算します j = 1 to m;
$$ y_ {inj} \:= \:\ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 −次の活性化関数を適用して出力を計算します
$$ y_ {j} \:= \:f(y_ {inj})\:= \:\ begin {cases} + 1&if \:y_ {inj} \:> \:0 \\ 0&if \ :y_ {inj} \:= \:0 \\-1&if \:y_ {inj} \:<\:0 \ end {cases} $$