ベクトル量子化の学習

ベクトル量子化（VQ）やKohonen自己組織化マップ（KSOM）とは異なり、学習ベクトル量子化（LVQ）は、基本的に教師あり学習を使用する競争力のあるネットワークです。これは、各出力ユニットがクラスを表すパターンを分類するプロセスとして定義できます。教師あり学習を使用するため、ネットワークには、出力クラスの初期分布とともに、既知の分類を持つ一連のトレーニングパターンが与えられます。トレーニングプロセスの完了後、LVQは、入力ベクトルを出力ユニットと同じクラスに割り当てることにより、入力ベクトルを分類します。

建築

次の図は、KSOMのアーキテクチャと非常によく似たLVQのアーキテクチャを示しています。ご覧のとおり、“n” 入力ユニットの数と “m”出力ユニットの数。レイヤーは完全に相互接続されており、ウェイトがあります。

使用されるパラメータ

以下は、LVQトレーニングプロセスとフローチャートで使用されるパラメーターです。

x=トレーニングベクトル（x ₁、...、x _i、...、x _n）
T =トレーニングベクトルのクラス x
w_j =の重みベクトル j^th 出力ユニット
C_j =に関連付けられたクラス j^th 出力ユニット

トレーニングアルゴリズム

Step 1 −参照ベクトルを初期化します。これは次のように実行できます。

Step 1(a) −与えられたトレーニングベクトルのセットから、最初の「m」（クラスターの数）トレーニングベクトルとそれらを重みベクトルとして使用します。残りのベクトルはトレーニングに使用できます。
Step 1(b) −初期の重みと分類をランダムに割り当てます。
Step 1(c) −K-meansクラスタリング法を適用します。

Step 2 −参照ベクトル$ \ alpha $を初期化します

Step 3 −このアルゴリズムを停止するための条件が満たされない場合は、手順4〜9に進みます。

Step 4 −すべてのトレーニング入力ベクトルについて手順5〜6に従います x。

Step 5 −のユークリッド距離の2乗を計算する j = 1 to m そして i = 1 to n

$$ D（j）\：= \：\ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m（x_ {i} \：-\：w_ {ij }）^ 2 $$

Step 6 −勝利ユニットを獲得する J どこ D(j) 最小です。

Step 7 −次の関係により、勝利ユニットの新しい重量を計算します。

もし T = C_j 次に$ w_ {j}（new）\：= \：w_ {j}（old）\：+ \：\ alpha [x \：-\：w_ {j}（old）] $

もし T ≠ C_j 次に$ w_ {j}（new）\：= \：w_ {j}（old）\：-\：\ alpha [x \：-\：w_ {j}（old）] $

Step 8 −学習率$ \ alpha $を減らします。

Step 9−停止状態をテストします。次のようになります-

到達したエポックの最大数。
学習率は無視できる値に減少しました。

フローチャート

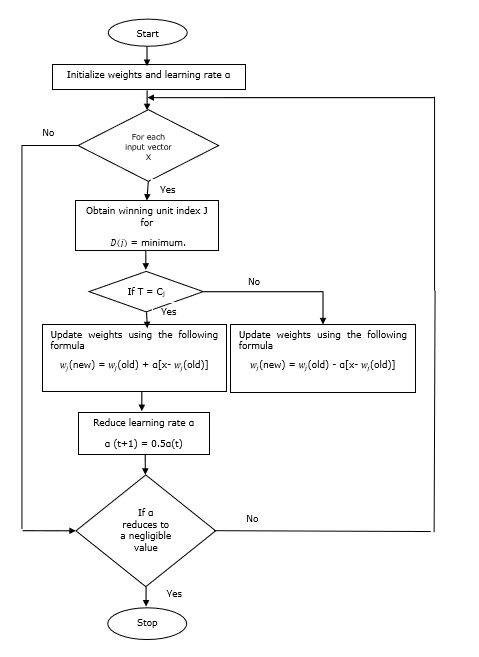
バリアント

他の3つのバリアント、つまりLVQ2、LVQ2.1、およびLVQ3は、Kohonenによって開発されました。勝者と次点のユニットが学習するという概念による、これら3つのバリアントすべての複雑さは、LVQよりも複雑です。

LVQ2

上記のLVQの他のバリアントの概念で説明したように、LVQ2の条件はウィンドウによって形成されます。このウィンドウは、次のパラメータに基づいています-

x −現在の入力ベクトル
y_c −に最も近い参照ベクトル x
y_r −次に近い他の参照ベクトル x
d_c −からの距離 x に y_c
d_r −からの距離 x に y_r

入力ベクトル x 窓に落ちる場合

$$ \ frac {d_ {c}} {d_ {r}} \：> \：1 \：-\：\ theta \：\：and \：\：\ frac {d_ {r}} {d_ {c }} \：> \：1 \：+ \：\ theta $$

ここで、$ \ theta $はトレーニングサンプルの数です。

更新は次の式で行うことができます-

$ y_ {c}（t \：+ \：1）\：= \：y_ {c}（t）\：+ \：\ alpha（t）[x（t）\：-\：y_ {c} （t）] $ (belongs to different class)

$ y_ {r}（t \：+ \：1）\：= \：y_ {r}（t）\：+ \：\ alpha（t）[x（t）\：-\：y_ {r} （t）] $ (belongs to same class)

ここで$ \ alpha $は学習率です。

LVQ2.1

LVQ2.1では、最も近い2つのベクトルを使用します。 y_c1 そして y_c2 ウィンドウの条件は次のとおりです。

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}、\ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \：> \ :( 1 \ ：-\：\ theta）$$

$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}、\ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \：<\ :( 1 \ ：+ \：\ theta）$$

更新は次の式で行うことができます-

$ y_ {c1}（t \：+ \：1）\：= \：y_ {c1}（t）\：+ \：\ alpha（t）[x（t）\：-\：y_ {c1} （t）] $ (belongs to different class)

$ y_ {c2}（t \：+ \：1）\：= \：y_ {c2}（t）\：+ \：\ alpha（t）[x（t）\：-\：y_ {c2} （t）] $ (belongs to same class)

ここで、$ \ alpha $は学習率です。

LVQ3

LVQ3では、最も近い2つのベクトルを使用します。 y_c1 そして y_c2 ウィンドウの条件は次のとおりです。

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}、\ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \：> \ :( 1 \ ：-\：\ theta）（1 \：+ \：\ theta）$$

ここで$ \ theta \約0.2 $

更新は次の式で行うことができます-

$ y_ {c1}（t \：+ \：1）\：= \：y_ {c1}（t）\：+ \：\ beta（t）[x（t）\：-\：y_ {c1} （t）] $ (belongs to different class)

$ y_ {c2}（t \：+ \：1）\：= \：y_ {c2}（t）\：+ \：\ beta（t）[x（t）\：-\：y_ {c2} （t）] $ (belongs to same class)

ここで、$ \ beta $は学習率$ \ alpha $の倍数です。 $\beta\:=\:m \alpha(t)$ すべてのための 0.1 < m < 0.5