Kohonen自己組織化機能マップ

任意の次元のパターンがあるとしますが、1次元または2次元でそれらが必要です。次に、特徴マッピングのプロセスは、広いパターン空間を典型的な特徴空間に変換するのに非常に役立ちます。さて、なぜ自己組織化特徴マップが必要なのかという疑問が生じます。その理由は、任意の次元を1次元または2次元に変換する機能に加えて、隣接トポロジを保持する機能も必要であるためです。

KohonenSOMの隣接トポロジ

さまざまなトポロジがありますが、次の2つのトポロジが最もよく使用されます-

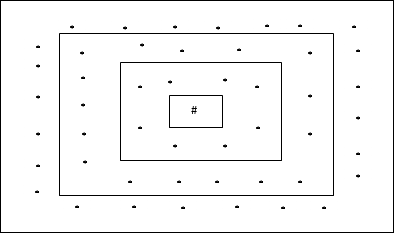
長方形グリッドトポロジ

このトポロジには、距離2グリッドに24ノード、距離1グリッドに16ノード、距離0グリッドに8ノードがあります。つまり、各長方形グリッド間の差は8ノードです。勝ったユニットは＃で示されます。

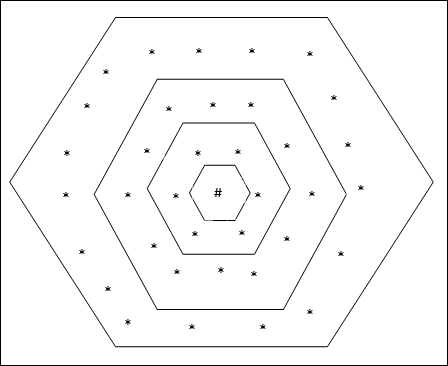
六角形のグリッドトポロジ

このトポロジには、距離2グリッドに18ノード、距離1グリッドに12ノード、距離0グリッドに6ノードがあります。つまり、各長方形グリッド間の差は6ノードです。勝ったユニットは＃で示されます。

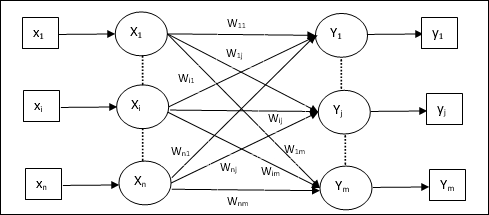
建築

KSOMのアーキテクチャは、競合ネットワークのアーキテクチャと似ています。前に説明した近隣スキームの助けを借りて、トレーニングはネットワークの拡張領域で実行できます。

トレーニングのアルゴリズム

Step 1 −重み、学習率を初期化します α と近隣のトポロジースキーム。

Step 2 −停止条件が真でない場合は、手順3〜9を続行します。

Step 3 −すべての入力ベクトルに対してステップ4-6を続行します x。

Step 4 −のユークリッド距離の2乗を計算する j = 1 to m

$$ D（j）\：= \：\ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m（x_ {i} \：-\：w_ {ij }）^ 2 $$

Step 5 −勝利ユニットを獲得する J どこ D(j) 最小です。

Step 6 −次の関係により、勝利ユニットの新しい重量を計算します。

$$ w_ {ij}（new）\：= \：w_ {ij}（old）\：+ \：\ alpha [x_ {i} \：-\：w_ {ij}（old）] $$

Step 7 −学習率を更新する α 次の関係で-

$$ \ alpha（t \：+ \：1）\：= \：0.5 \ alpha t $$

Step 8 −トポロジスキームの半径を小さくします。

Step 9 −ネットワークの停止状態を確認してください。