教師あり学習
名前が示すように、 supervised learning教師の監督の下で行われます。この学習プロセスは依存しています。教師あり学習の下でのANNのトレーニング中に、入力ベクトルがネットワークに提示され、ネットワークが出力ベクトルを生成します。この出力ベクトルは、目的の/ターゲット出力ベクトルと比較されます。実際の出力と目的/ターゲットの出力ベクトルの間に差がある場合、エラー信号が生成されます。このエラー信号に基づいて、実際の出力が目的の出力と一致するまで重みが調整されます。
パーセプトロン
パーセプトロンは、マッカロックとピッツのモデルを使用してフランクローゼンブラットによって開発された、人工ニューラルネットワークの基本的な操作単位です。教師あり学習ルールを採用し、データを2つのクラスに分類できます。
パーセプトロンの動作特性:任意の数の入力と調整可能な重みを持つ単一のニューロンで構成されますが、ニューロンの出力はしきい値に応じて1または0になります。また、重みが常に1であるバイアスで構成されます。次の図は、パーセプトロンの概略図を示しています。
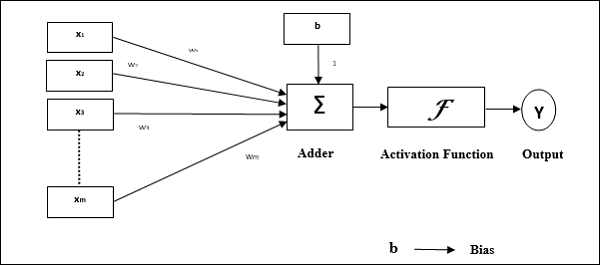
したがって、パーセプトロンには次の3つの基本要素があります。
Links −常に重み1を持つバイアスを含む重みを運ぶ接続リンクのセットがあります。
Adder −それぞれの重みを掛けた後、入力を追加します。
Activation function−ニューロンの出力を制限します。最も基本的な活性化関数は、2つの可能な出力を持つヘヴィサイドの階段関数です。この関数は、入力が正の場合は1を返し、負の入力の場合は0を返します。
トレーニングアルゴリズム
パーセプトロンネットワークは、単一の出力ユニットと複数の出力ユニット用にトレーニングできます。
単一出力ユニットのトレーニングアルゴリズム
Step 1 −以下を初期化してトレーニングを開始します−
- Weights
- Bias
- 学習率$ \ alpha $
計算を簡単にし、簡単にするために、重みとバイアスを0に設定し、学習率を1に設定する必要があります。
Step 2 −停止条件が真でない場合は、手順3〜8を続行します。
Step 3 −トレーニングベクトルごとに手順4〜6を続行します x。
Step 4 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 5 −ここで、次の関係で正味入力を取得します−
$$ y_ {in} \:= \:b \:+ \:\ displaystyle \ sum \ limits_ {i} ^ n x_ {i}。\:w_ {i} $$
ここに ‘b’ バイアスであり、 ‘n’ 入力ニューロンの総数です。
Step 6 −次の活性化関数を適用して、最終出力を取得します。
$$ f(y_ {in})\:= \:\ begin {cases} 1&if \:y_ {in} \:> \:\ theta \\ 0&if \:-\ theta \:\ leqslant \ :y_ {in} \:\ leqslant \:\ theta \\-1&if \:y_ {in} \:<\:-\ theta \ end {cases} $$
Step 7 −次のように重量とバイアスを調整します−
Case 1 −もし y ≠ t その後、
$$ w_ {i}(new)\:= \:w_ {i}(old)\:+ \:\ alpha \:tx_ {i} $$
$$ b(new)\:= \:b(old)\:+ \:\ alpha t $$
Case 2 −もし y = t その後、
$$ w_ {i}(新)\:= \:w_ {i}(旧)$$
$$ b(新)\:= \:b(旧)$$
ここに ‘y’ 実際の出力であり、 ‘t’ 目的の/ターゲット出力です。
Step 8 −重量に変化がない場合に発生する停止状態をテストします。
複数の出力ユニットのトレーニングアルゴリズム
次の図は、複数の出力クラスのパーセプトロンのアーキテクチャです。
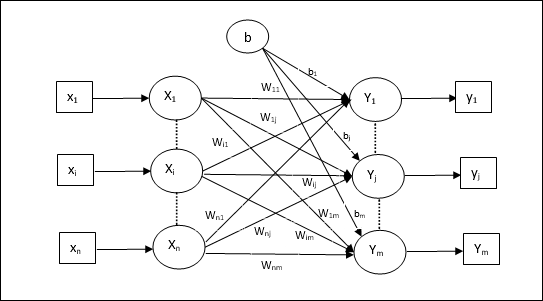
Step 1 −以下を初期化してトレーニングを開始します−
- Weights
- Bias
- 学習率$ \ alpha $
計算を簡単にし、簡単にするために、重みとバイアスを0に設定し、学習率を1に設定する必要があります。
Step 2 −停止条件が真でない場合は、手順3〜8を続行します。
Step 3 −トレーニングベクトルごとに手順4〜6を続行します x。
Step 4 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 5 −次の関係で正味入力を取得します−
$$ y_ {in} \:= \:b \:+ \:\ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \:w_ {ij} $$
ここに ‘b’ バイアスであり、 ‘n’ 入力ニューロンの総数です。
Step 6 −次の活性化関数を適用して、各出力ユニットの最終出力を取得します j = 1 to m −
$$ f(y_ {in})\:= \:\ begin {cases} 1&if \:y_ {inj} \:> \:\ theta \\ 0&if \:-\ theta \:\ leqslant \ :y_ {inj} \:\ leqslant \:\ theta \\-1&if \:y_ {inj} \:<\:-\ theta \ end {cases} $$
Step 7 −重量とバイアスを調整します x = 1 to n そして j = 1 to m 次のように-
Case 1 −もし yj ≠ tj その後、
$$ w_ {ij}(new)\:= \:w_ {ij}(old)\:+ \:\ alpha \:t_ {j} x_ {i} $$
$$ b_ {j}(new)\:= \:b_ {j}(old)\:+ \:\ alpha t_ {j} $$
Case 2 −もし yj = tj その後、
$$ w_ {ij}(新)\:= \:w_ {ij}(旧)$$
$$ b_ {j}(新)\:= \:b_ {j}(旧)$$
ここに ‘y’ 実際の出力であり、 ‘t’ 目的の/ターゲット出力です。
Step 8 −重量に変化がない場合に発生する停止状態をテストします。
適応線形ニューロン(アダリン)
Adaptive Linear Neuronの略であるAdalineは、単一の線形ユニットを持つネットワークです。1960年にWidrowとHoffによって開発されました。Adalineに関するいくつかの重要なポイントは次のとおりです。
バイポーラ活性化関数を使用しています。
トレーニングにデルタルールを使用して、実際の出力と目的の/ターゲット出力の間の平均二乗誤差(MSE)を最小化します。
重みとバイアスは調整可能です。
建築
Adalineの基本構造は、実際の出力が目的の/ターゲット出力と比較される助けを借りて、追加のフィードバックループを持つパーセプトロンに似ています。トレーニングアルゴリズムに基づいて比較した後、重みとバイアスが更新されます。
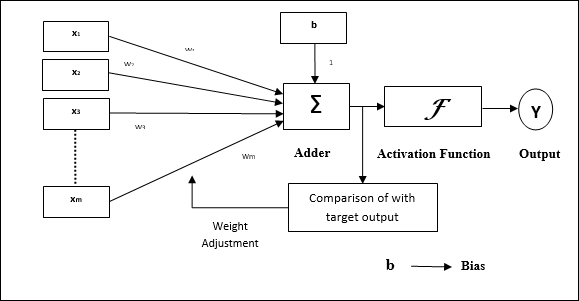
トレーニングアルゴリズム
Step 1 −以下を初期化してトレーニングを開始します−
- Weights
- Bias
- 学習率$ \ alpha $
計算を簡単にし、簡単にするために、重みとバイアスを0に設定し、学習率を1に設定する必要があります。
Step 2 −停止条件が真でない場合は、手順3〜8を続行します。
Step 3 −すべてのバイポーラトレーニングペアについて手順4〜6を続行します s:t。
Step 4 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 5 −次の関係で正味入力を取得します−
$$ y_ {in} \:= \:b \:+ \:\ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \:w_ {i} $$
ここに ‘b’ バイアスであり、 ‘n’ 入力ニューロンの総数です。
Step 6 −次の活性化関数を適用して、最終出力を取得します−
$$ f(y_ {in})\:= \:\ begin {cases} 1&if \:y_ {in} \:\ geqslant \:0 \\-1&if \:y_ {in} \:< \:0 \ end {cases} $$
Step 7 −次のように重量とバイアスを調整します−
Case 1 −もし y ≠ t その後、
$$ w_ {i}(new)\:= \:w_ {i}(old)\:+ \:\ alpha(t \:-\:y_ {in})x_ {i} $$
$$ b(new)\:= \:b(old)\:+ \:\ alpha(t \:-\:y_ {in})$$
Case 2 −もし y = t その後、
$$ w_ {i}(新)\:= \:w_ {i}(旧)$$
$$ b(新)\:= \:b(旧)$$
ここに ‘y’ 実際の出力であり、 ‘t’ 目的の/ターゲット出力です。
$(t \:-\; y_ {in})$は計算されたエラーです。
Step 8 −体重に変化がない場合、またはトレーニング中に発生した最大の体重変化が指定された許容値よりも小さい場合に発生する停止条件をテストします。
複数の適応線形ニューロン(マダリン)
Multiple Adaptive Linear Neuronの略であるMadalineは、多数のAdalineを並列に構成するネットワークです。単一の出力ユニットがあります。マダリンに関するいくつかの重要なポイントは次のとおりです-
これは多層パーセプトロンのようなもので、Adalineは入力とMadalineレイヤーの間の隠れたユニットとして機能します。
Adalineアーキテクチャで見られるように、入力レイヤーとAdalineレイヤーの間の重みとバイアスは調整可能です。
AdalineレイヤーとMadalineレイヤーの重みとバイアスは1に固定されています。
トレーニングはデルタルールの助けを借りて行うことができます。
建築
マダリンのアーキテクチャは、 “n” 入力層のニューロン、 “m”アダリン層のニューロン、およびマダリン層の1つのニューロン。Adalineレイヤーは、入力レイヤーと出力レイヤー、つまりMadalineレイヤーの間にあるため、非表示レイヤーと見なすことができます。
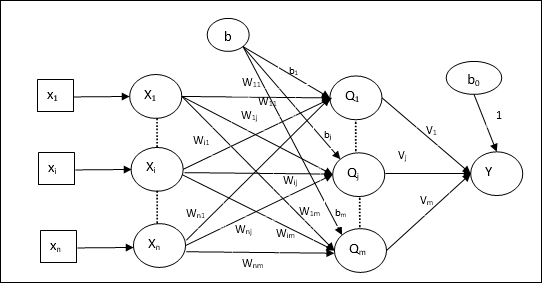
トレーニングアルゴリズム
これで、入力層とAdaline層の間の重みとバイアスのみが調整され、Adaline層とMadaline層の間の重みとバイアスが固定されることがわかりました。
Step 1 −以下を初期化してトレーニングを開始します−
- Weights
- Bias
- 学習率$ \ alpha $
計算を簡単にし、簡単にするために、重みとバイアスを0に設定し、学習率を1に設定する必要があります。
Step 2 −停止条件が真でない場合は、手順3〜8を続行します。
Step 3 −すべてのバイポーラトレーニングペアについて手順4〜6を続行します s:t。
Step 4 −各入力ユニットを次のようにアクティブにします−
$$ x_ {i} \:= \:s_ {i} \ :( i \:= \:1 \:to \:n)$$
Step 5 −各隠れ層、つまり次の関係を持つAdaline層で正味入力を取得します。
$$ Q_ {inj} \:= \:b_ {j} \:+ \:\ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \:w_ {ij} \:\:\:j \: = \:1 \:to \:m $$
ここに ‘b’ バイアスであり、 ‘n’ 入力ニューロンの総数です。
Step 6 −次の活性化関数を適用して、AdalineおよびMadalineレイヤーで最終出力を取得します。
$$ f(x)\:= \:\ begin {cases} 1&if \:x \:\ geqslant \:0 \\-1&if \:x \:<\:0 \ end {cases} $ $
隠し(アダリン)ユニットでの出力
$$ Q_ {j} \:= \:f(Q_ {inj})$$
ネットワークの最終出力
$$ y \:= \:f(y_ {in})$$
i.e. $ \:\:y_ {inj} \:= \:b_ {0} \:+ \:\ sum_ {j = 1} ^ m \:Q_ {j} \:v_ {j} $
Step 7 −誤差を計算し、次のように重みを調整します−
Case 1 −もし y ≠ t そして t = 1 その後、
$$ w_ {ij}(new)\:= \:w_ {ij}(old)\:+ \:\ alpha(1 \:-\:Q_ {inj})x_ {i} $$
$$ b_ {j}(new)\:= \:b_ {j}(old)\:+ \:\ alpha(1 \:-\:Q_ {inj})$$
この場合、重みはで更新されます Qj ここで、正味入力は0に近いです。 t = 1。
Case 2 −もし y ≠ t そして t = -1 その後、
$$ w_ {ik}(new)\:= \:w_ {ik}(old)\:+ \:\ alpha(-1 \:-\:Q_ {ink})x_ {i} $$
$$ b_ {k}(new)\:= \:b_ {k}(old)\:+ \:\ alpha(-1 \:-\:Q_ {ink})$$
この場合、重みはで更新されます Qk ここで、正味入力は正です。 t = -1。
ここに ‘y’ 実際の出力であり、 ‘t’ 目的の/ターゲット出力です。
Case 3 −もし y = t その後
重みに変化はありません。
Step 8 −体重に変化がない場合、またはトレーニング中に発生した最大の体重変化が指定された許容値よりも小さい場合に発生する停止条件をテストします。
バックプロパゲーションニューラルネットワーク
バックプロパゲーションニューラル(BPN)は、入力層、少なくとも1つの隠れ層、および出力層で構成される多層ニューラルネットワークです。その名前が示すように、バックプロパゲーションはこのネットワークで行われます。ターゲット出力と実際の出力を比較することによって出力層で計算されたエラーは、入力層に向かって伝播されます。
建築
図に示すように、BPNのアーキテクチャには、重みを持つ3つの相互接続されたレイヤーがあります。隠れ層と出力層にもバイアスがあり、その重みは常に1です。図から明らかなように、BPNの動作は2つのフェーズに分かれています。一方のフェーズは入力層から出力層に信号を送信し、もう一方のフェーズはエラーを出力層から入力層に逆伝播します。

トレーニングアルゴリズム
トレーニングでは、BPNはバイナリシグモイド活性化関数を使用します。BPNのトレーニングには、次の3つのフェーズがあります。
Phase 1 −フィードフォワードフェーズ
Phase 2 −エラーのバックプロパゲーション
Phase 3 −重みの更新
これらのすべてのステップは、次のようにアルゴリズムで終了します
Step 1 −以下を初期化してトレーニングを開始します−
- Weights
- 学習率$ \ alpha $
計算を簡単にし、簡単にするために、いくつかの小さなランダムな値を取ります。
Step 2 −停止条件が真でない場合は、ステップ3-11を続行します。
Step 3 −トレーニングペアごとに手順4〜10を続行します。
フェーズ1
Step 4 −各入力ユニットは入力信号を受信します xi そしてそれをすべての隠されたユニットに送ります i = 1 to n
Step 5 −次の関係を使用して、隠れユニットでの正味入力を計算します。
$$ Q_ {inj} \:= \:b_ {0j} \:+ \:\ sum_ {i = 1} ^ n x_ {i} v_ {ij} \:\:\:\:j \:= \ :1 \:to \:p $$
ここに b0j 隠されたユニットへのバイアスです、 vij の重みは j から来る隠された層の単位 i 入力レイヤーの単位。
次に、次の活性化関数を適用して、正味出力を計算します。
$$ Q_ {j} \:= \:f(Q_ {inj})$$
隠れ層ユニットのこれらの出力信号を出力層ユニットに送信します。
Step 6 −次の関係を使用して、出力層ユニットでの正味入力を計算します。
$$ y_ {ink} \:= \:b_ {0k} \:+ \:\ sum_ {j = 1} ^ p \:Q_ {j} \:w_ {jk} \:\:k \:= \ :1 \:to \:m $$
ここに b0k は出力ユニットのバイアスです。 wjk の重みは k から来る出力層の単位 j 隠れ層の単位。
次の活性化関数を適用して、正味出力を計算します
$$ y_ {k} \:= \:f(y_ {ink})$$
フェーズ2
Step 7 −各出力ユニットで受信したターゲットパターンに対応して、次のように誤り訂正項を計算します。
$$ \ delta_ {k} \:= \ :( t_ {k} \:-\:y_ {k})f ^ {'}(y_ {ink})$$
これに基づいて、重みとバイアスを次のように更新します-
$$ \ Delta v_ {jk} \:= \:\ alpha \ delta_ {k} \:Q_ {ij} $$
$$ \ Delta b_ {0k} \:= \:\ alpha \ delta_ {k} $$
次に、$ \ delta_ {k} $を非表示レイヤーに送り返します。
Step 8 −これで、各非表示ユニットは、出力ユニットからのデルタ入力の合計になります。
$$ \ delta_ {inj} \:= \:\ displaystyle \ sum \ limits_ {k = 1} ^ m \ delta_ {k} \:w_ {jk} $$
誤差項は次のように計算できます-
$$ \ delta_ {j} \:= \:\ delta_ {inj} f ^ {'}(Q_ {inj})$$
これに基づいて、重みとバイアスを次のように更新します-
$$ \ Delta w_ {ij} \:= \:\ alpha \ delta_ {j} x_ {i} $$
$$ \ Delta b_ {0j} \:= \:\ alpha \ delta_ {j} $$
フェーズ3
Step 9 −各出力ユニット (ykk = 1 to m) 重みとバイアスを次のように更新します-
$$ v_ {jk}(new)\:= \:v_ {jk}(old)\:+ \:\ Delta v_ {jk} $$
$$ b_ {0k}(新しい)\:= \:b_ {0k}(古い)\:+ \:\ Deltab_ {0k} $$
Step 10 −各出力ユニット (zjj = 1 to p) 重みとバイアスを次のように更新します-
$$ w_ {ij}(new)\:= \:w_ {ij}(old)\:+ \:\ Delta w_ {ij} $$
$$ b_ {0j}(new)\:= \:b_ {0j}(old)\:+ \:\ Delta b_ {0j} $$
Step 11 −停止条件を確認します。これは、到達したエポック数であるか、ターゲット出力が実際の出力と一致している可能性があります。
一般化されたデルタ学習ルール
デルタルールは、出力レイヤーに対してのみ機能します。一方、一般化されたデルタルールは、back-propagation ルールは、非表示レイヤーの目的の値を作成する方法です。
数学的定式化
活性化関数$ y_ {k} \:= \:f(y_ {ink})$の場合、非表示層と出力層での正味入力の導関数は次の式で与えられます。
$$ y_ {ink} \:= \:\ displaystyle \ sum \ limits_i \:z_ {i} w_ {jk} $$
そして$ \:\:y_ {inj} \:= \:\ sum_i x_ {i} v_ {ij} $
今、最小化する必要があるエラーは
$$ E \:= \:\ frac {1} {2} \ displaystyle \ sum \ limits_ {k} \:[t_ {k} \:-\:y_ {k}] ^ 2 $$
連鎖律を使用することにより、
$$ \ frac {\ partial E} {\ partial w_ {jk}} \:= \:\ frac {\ partial} {\ partial w_ {jk}}(\ frac {1} {2} \ displaystyle \ sum \ Limits_ {k} \:[t_ {k} \:-\:y_ {k}] ^ 2)$$
$$ = \:\ frac {\ partial} {\ partial w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \:-\:t(y_ {ink})] ^ 2 \ rgroup $$
$$ = \:-[t_ {k} \:-\:y_ {k}] \ frac {\ partial} {\ partial w_ {jk}} f(y_ {ink})$$
$$ = \:-[t_ {k} \:-\:y_ {k}] f(y_ {ink})\ frac {\ partial} {\ partial w_ {jk}}(y_ {ink})$$
$$ = \:-[t_ {k} \:-\:y_ {k}] f ^ {'}(y_ {ink})z_ {j} $$
ここで、$ \ delta_ {k} \:= \:-[t_ {k} \:-\:y_ {k}] f ^ {'}(y_ {ink})$としましょう。
隠しユニットへの接続の重み zj −で与えることができます
$$ \ frac {\ partial E} {\ partial v_ {ij}} \:= \:-\ displaystyle \ sum \ limits_ {k} \ delta_ {k} \ frac {\ partial} {\ partial v_ {ij} } \ :( y_ {ink})$$
$ y_ {ink} $の値を入力すると、次のようになります。
$$ \ delta_ {j} \:= \:-\ displaystyle \ sum \ limits_ {k} \ delta_ {k} w_ {jk} f ^ {'}(z_ {inj})$$
体重の更新は次のように行うことができます-
出力ユニットの場合-
$$ \ Delta w_ {jk} \:= \:-\ alpha \ frac {\ partial E} {\ partial w_ {jk}} $$
$$ = \:\ alpha \:\ delta_ {k} \:z_ {j} $$
隠しユニットの場合-
$$ \ Delta v_ {ij} \:= \:-\ alpha \ frac {\ partial E} {\ partial v_ {ij}} $$
$$ = \:\ alpha \:\ delta_ {j} \:x_ {i} $$