人工ニューラルネットワーク-遺伝的アルゴリズム

自然は常にすべての人類にとって素晴らしいインスピレーションの源でした。遺伝的アルゴリズム（GA）は、自然淘汰と遺伝学の概念に基づく検索ベースのアルゴリズムです。GAは、次のように知られるはるかに大きな計算ブランチのサブセットです。Evolutionary Computation。

GAは、ミシガン大学のJohn Hollandと彼の学生および同僚、特にDavid E. Goldbergによって開発され、それ以来、さまざまな最適化問題で試行され、高い成功を収めています。

GAには、特定の問題に対する可能な解決策のプールまたは母集団があります。次に、これらのソリューションは（自然遺伝学のように）組換えと突然変異を受け、新しい子供を生み出し、このプロセスはさまざまな世代にわたって繰り返されます。各個体（または候補解）には（その目的関数値に基づいて）適応度値が割り当てられ、より適切な個体には、より多くの「より適切な」個体を交配して産出する可能性が高くなります。これは、ダーウィンの「適者生存」の理論と一致しています。

このようにして、停止基準に達するまで、世代を超えてより優れた個人またはソリューションを「進化」させ続けます。

遺伝的アルゴリズムは本質的に十分にランダム化されていますが、履歴情報も活用するため、ランダムローカル検索（さまざまなランダムソリューションを試し、これまでの最良のものを追跡する）よりもはるかに優れたパフォーマンスを発揮します。

GAの利点

GAにはさまざまな利点があり、非常に人気があります。これらには以下が含まれます-

派生情報は必要ありません（多くの実際の問題では利用できない場合があります）。
従来の方法と比較して、より高速で効率的です。
非常に優れた並列機能を備えています。
連続関数と離散関数の両方、および多目的問題を最適化します。
単一のソリューションだけでなく、「優れた」ソリューションのリストを提供します。
問題に対する答えは常に得られますが、時間の経過とともに改善されます。
検索スペースが非常に大きく、関連するパラメーターが多数ある場合に役立ちます。

GAの制限

他の手法と同様に、GAにもいくつかの制限があります。これらには以下が含まれます-

GAは、すべての問題、特に単純で派生情報が利用可能な問題に適しているわけではありません。
適応度の値は繰り返し計算されますが、問題によっては計算コストが高くなる可能性があります。
確率論的であるため、ソリューションの最適性や品質は保証されません。
適切に実装されていない場合、GAは最適なソリューションに収束しない可能性があります。

GA –動機

遺伝的アルゴリズムには、「十分な」ソリューションを「十分な速さ」で提供する機能があります。これにより、Gasは最適化問題の解決に使用するのに魅力的です。GAが必要な理由は次のとおりです。

難しい問題の解決

コンピュータサイエンスには、さまざまな問題があります。 NP-Hard。これが本質的に意味することは、最も強力なコンピューティングシステムでさえ、その問題を解決するのに非常に長い時間（さらには数年！）かかるということです。このようなシナリオでは、GAは提供するための効率的なツールであることが証明されていますusable near-optimal solutions 短時間で。

グラジエントベースのメソッドの失敗

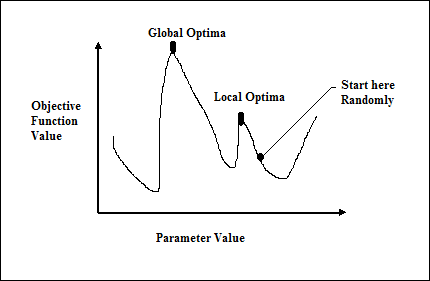
従来の微積分ベースの方法は、ランダムなポイントから開始し、丘の頂上に到達するまで勾配の方向に移動することによって機能します。この手法は効率的であり、線形回帰のコスト関数などの単一ピークの目的関数に非常に適しています。ただし、ほとんどの実際の状況では、ランドスケープと呼ばれる非常に複雑な問題があり、多くの山と谷で構成されています。これにより、図に示すように、局所的な最適点でスタックする固有の傾向があるため、このような方法は失敗します。次の図で。

優れたソリューションを迅速に入手

巡回セールスマン問題（TSP）のようないくつかの難しい問題には、経路探索やVLSI設計などの実際のアプリケーションがあります。ここで、GPSナビゲーションシステムを使用していて、送信元から宛先までの「最適な」パスを計算するのに数分（または数時間）かかると想像してください。このような実際のアプリケーションでの遅延は許容できないため、「高速」で提供される「十分な」ソリューションが必要です。