ボルツマンマシン

これらは、反復構造を持つ確率的学習プロセスであり、ANNで使用される初期の最適化手法の基礎です。ボルツマンマシンは、1985年にジェフリーヒントンとテリーセジュノスキーによって発明されました。ボルツマンマシンのヒントンの言葉を見ると、より明確になります。

「このネットワークの驚くべき機能は、ローカルで利用可能な情報のみを使用することです。重量の変化は、接続する2つのユニットの動作にのみ依存しますが、変化によってグローバルな測定値が最適化されます」-Ackley、Hinton1985。

ボルツマンマシンに関するいくつかの重要なポイント-

それらは反復構造を使用します。
それらは確率的ニューロンで構成され、1または0の2つの可能な状態のいずれかを持ちます。
この中のニューロンのいくつかは適応性があり（自由状態）、いくつかはクランプされています（凍結状態）。
離散ホップフィールドネットワークにシミュレーテッドアニーリングを適用すると、ボルツマンマシンになります。

ボルツマンマシンの目的

ボルツマンマシンの主な目的は、問題の解決を最適化することです。その特定の問題に関連する重量と量を最適化するのはボルツマンマシンの仕事です。

建築

次の図は、ボルツマンマシンのアーキテクチャを示しています。図から明らかなように、これは2次元の単位配列です。ここで、ユニット間の相互接続の重みは–p どこ p > 0。自己接続の重みは次の式で与えられます。b どこ b > 0。

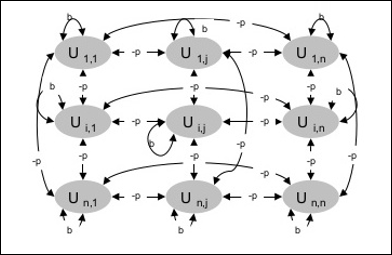
トレーニングアルゴリズム

ボルツマンマシンの重みは固定されていることがわかっているため、ネットワーク内の重みを更新する必要がないため、トレーニングアルゴリズムはありません。ただし、ネットワークをテストするには、重みを設定し、コンセンサス関数（CF）を見つける必要があります。

ボルツマンマシンには一連のユニットがあります U_i そして U_j 双方向接続があります。

固定重量を検討しています w_ij。
w_ij ≠ 0 もし U_i そして U_j 接続されています。
加重相互接続にも対称性があります。 w_ij = w_ji。
w_ii また、ユニット間の自己接続が存在します。
任意のユニット用 U_i、その状態 u_i 1または0のいずれかになります。

ボルツマンマシンの主な目的は、次の関係によって与えられるコンセンサス関数（CF）を最大化することです。

$$ CF \：= \：\ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

ここで、状態が1から0または0から1に変化すると、コンセンサスの変化は次の関係で与えられます。

$$ \ Delta CF \：= \ :( 1 \：-\：2u_ {i}）（w_ {ij} \：+ \：\ displaystyle \ sum \ extends_ {j \ neq i} u_ {i} w_ { ij}）$$

ここに u_i の現在の状態です U_i。

係数の変動（1 - 2u_i）は次の関係で与えられます-

$$（1 \：-\：2u_ {i}）\：= \：\ begin {cases} + 1、＆U_ {i} \：is \：currently \：off \\-1、＆U_ {i } \：is \：currently \：on \ end {cases} $$

一般的に、ユニット U_i状態は変更されませんが、変更された場合、情報はユニットのローカルに存在します。その変更に伴い、ネットワークのコンセンサスも向上します。

ユニットの状態の変化を受け入れるネットワークの確率は、次の関係によって与えられます。

$$ AF（i、T）\：= \：\ frac {1} {1 \：+ \：exp [-\ frac {\ Delta CF（i）} {T}]} $$

ここに、 T制御パラメータです。CFが最大値に達すると減少します。

テストアルゴリズム

Step 1 −以下を初期化してトレーニングを開始します−

問題の制約を表す重み
制御パラメータT

Step 2 −停止条件が真でない場合は、手順3〜8を続行します。

Step 3 −手順4〜7を実行します。

Step 4 −状態の1つが重みを変更したと想定し、整数を選択します I, J 間のランダム値として 1 そして n。

Step 5 −コンセンサスの変化を次のように計算します−

$$ \ Delta CF \：= \ :( 1 \：-\：2u_ {i}）（w_ {ij} \：+ \：\ displaystyle \ sum \ extends_ {j \ neq i} u_ {i} w_ { ij}）$$

Step 6 −このネットワークが状態の変化を受け入れる確率を計算します

$$ AF（i、T）\：= \：\ frac {1} {1 \：+ \：exp [-\ frac {\ Delta CF（i）} {T}]} $$

Step 7 −次のようにこの変更を承認または拒否します−

Case I −もし R < AF、変更を受け入れます。

Case II −もし R ≥ AF、変更を拒否します。

ここに、 R は0から1までの乱数です。

Step 8 −制御パラメータ（温度）を次のように下げます−

T(new) = ⁡0.95T(old)

Step 9 −次のような停止条件をテストします−

温度が指定値に達しました
指定された反復回数の間、状態に変化はありません。