学習と適応

先に述べたように、ANNは生物学的神経系、つまり人間の脳の働きに完全に触発されています。人間の脳の最も印象的な特徴は学習することです。したがって、同じ機能がANNによって取得されます。

ANNでの学習とは何ですか？

基本的に、学習とは、環境に変化があったときに、それ自体で変化を行い、適応させることを意味します。ANNは複雑なシステムであり、より正確には、通過する情報に基づいて内部構造を変更できる複雑な適応システムであると言えます。

どうしてそれが重要ですか？

複雑な適応システムであるため、ANNでの学習は、処理ユニットが環境の変化に応じて入出力動作を変更できることを意味します。特定のネットワークが構築されると、固定の活性化関数と入出力ベクトルのために、ANNでの学習の重要性が増します。ここで、入出力の動作を変更するには、重みを調整する必要があります。

分類

これは、同じクラスのサンプル間で共通の特徴を見つけることにより、サンプルのデータを異なるクラスに区別することを学習するプロセスとして定義できます。たとえば、ANNのトレーニングを実行するために、独自の機能を備えたトレーニングサンプルがいくつかあり、そのテストを実行するために、他の独自の機能を備えたテストサンプルがいくつかあります。分類は、教師あり学習の一例です。

ニューラルネットワーク学習ルール

ANN学習中に、入力/出力の動作を変更するには、重みを調整する必要があることがわかっています。したがって、重みを変更できる方法が必要です。これらの方法は学習ルールと呼ばれ、単にアルゴリズムまたは方程式です。以下はニューラルネットワークのいくつかの学習ルールです-

ヘッブの学習規則

このルールは、最も古く、最も単純なものの1つであり、1949年にドナルドヘッブの著書「 TheOrganization of Behavior」で紹介されました。これは、一種のフィードフォワード、教師なし学習です。

Basic Concept −このルールは、Hebbが書いた提案に基づいています−

「細胞Aの軸索が細胞Bを興奮させるのに十分近く、繰り返しまたは持続的に発火に関与すると、Bを発火する細胞の1つとして、Aの効率が向上するように、一方または両方の細胞で何らかの成長プロセスまたは代謝変化が起こります、増加します。」

上記の仮定から、ニューロンが同時に発火すると2つのニューロン間の接続が強化され、異なる時間に発火すると弱くなる可能性があると結論付けることができます。

Mathematical Formulation −ヘッブの学習規則によれば、次の式は、すべてのタイムステップで接続の重みを増やすための式です。

$$ \ Delta w_ {ji}（t）\：= \：\ alpha x_ {i}（t）.y_ {j}（t）$$

ここで、$ \ Delta w_ {ji}（t）$⁡=時間ステップで接続の重みが増加する増分 t

$ \ alpha $ =ポジティブで一定の学習率

$ x_ {i}（t）$ =タイムステップでのシナプス前ニューロンからの入力値 t

$ y_ {i}（t）$ =同じタイムステップでのシナプス前ニューロンの出力 t

パーセプトロン学習ルール

このルールは、Rosenblattによって導入された線形活性化関数を使用した単層フィードフォワードネットワークの教師あり学習アルゴリズムを修正するエラーです。

Basic Concept−本質的に監視されているため、エラーを計算するために、目的の/ターゲットの出力と実際の出力が比較されます。違いが見つかった場合は、接続の重みを変更する必要があります。

Mathematical Formulation −その数学的定式化を説明するために、「n」個の有限入力ベクトルx（n）と、その目的/ターゲット出力ベクトルt（n）があるとします。ここで、n = 1からNです。

これで、正味入力に基づいて前述したように、出力 'y'を計算でき、その正味入力に適用される活性化関数は次のように表すことができます。

$$ y \：= \：f（y_ {in}）\：= \：\ begin {cases} 1、＆y_ {in} \：> \：\ theta \\ 0、＆y_ {in} \： \ leqslant \：\ theta \ end {cases} $$

どこ θ はしきい値です。

重みの更新は、次の2つの場合に実行できます。

Case I −いつ t ≠ y、その後

$$ w（new）\：= \：w（old）\：+ \; tx $$

Case II −いつ t = y、その後

体重の変化なし

デルタ学習ルール（Widrow-Hoffルール）

これは、すべてのトレーニングパターンでエラーを最小限に抑えるために、最小平均二乗（LMS）メソッドとも呼ばれるBernardWidrowとMarcianHoffによって導入されました。これは、継続的な活性化関数を備えた一種の教師あり学習アルゴリズムです。

Basic Concept−このルールの基本は、最急降下法であり、これは永遠に続きます。デルタルールは、出力ユニットへの正味入力とターゲット値を最小化するようにシナプスの重みを更新します。

Mathematical Formulation −シナプスの重みを更新するために、デルタルールは次の式で与えられます。

$$ \ Delta w_ {i} \：= \：\ alpha \：。x_ {i} .e_ {j} $$

ここで、$ \ Delta w_ {i} $ = i^番目の⁡パターンの重みの変化。

$ \ alpha $ =ポジティブで一定の学習率。

$ x_ {i} $ =シナプス前ニューロンからの入力値。

$ e_ {j} $ = $（t \：-\：y_ {in}）$、目的の/ターゲット出力と実際の出力の差⁡$ y_ {in} $

上記のデルタルールは、単一の出力ユニットのみを対象としています。

重みの更新は、次の2つの場合に実行できます。

Case-I −いつ t ≠ y、その後

$$ w（new）\：= \：w（old）\：+ \：\ Delta w $$

Case-II −いつ t = y、その後

体重の変化なし

競争力のある学習ルール（勝者-すべて）

これは、出力ノードが入力パターンを表すために互いに競合しようとする教師なしトレーニングに関係しています。この学習ルールを理解するには、次のような競争ネットワークを理解する必要があります。

Basic Concept of Competitive Network−このネットワークは、出力間にフィードバック接続がある単層フィードフォワードネットワークのようなものです。出力間の接続は、点線で示されている抑制型です。これは、競合他社が自分自身をサポートしないことを意味します。

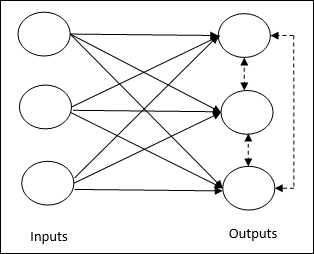
Basic Concept of Competitive Learning Rule−先に述べたように、出力ノード間で競合が発生します。したがって、主な概念は、トレーニング中に、特定の入力パターンに対して最も高いアクティベーションを持つ出力ユニットが勝者として宣言されるということです。このルールは、勝者のニューロンのみが更新され、残りのニューロンは変更されないままであるため、Winner-takes-allとも呼ばれます。

Mathematical formulation −この学習ルールを数学的定式化するための3つの重要な要素は次のとおりです−

Condition to be a winner −ニューロン$ y_ {k} $⁡⁡が勝者になりたい場合、次の条件が発生するとします。

$$ y_ {k} \：= \：\ begin {cases} 1＆if \：v_ {k} \：> \：v_ {j} \：for \：all \：j、\：j \：\ neq \：k \\ 0＆else \ end {cases} $$

つまり、$ y_ {k} $⁡などのニューロンが勝ちたい場合、その誘導された局所場（合計単位の出力）、たとえば$ v_ {k} $は、他のすべてのニューロンの中で最大でなければなりません。ネットワークで。

Condition of sum total of weight −競合学習ルールに対する別の制約は、特定の出力ニューロンに対する重みの合計が1になることです。たとえば、ニューロンを考慮する場合 k 次に−

$$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \：= \：1 \：\：\：\：\：\：\：\：\：for \：all \：k $$

Change of weight for winner−ニューロンが入力パターンに応答しない場合、そのニューロンでは学習は行われません。ただし、特定のニューロンが勝った場合、対応する重みは次のように調整されます。

$$ \ Delta w_ {kj} \：= \：\ begin {cases}-\ alpha（x_ {j} \：-\：w_ {kj}）、＆if \：neuron \：k \：wins \\ 0、＆if \：neuron \：k \：losses \ end {cases} $$

ここで$ \ alpha $は学習率です。

これは、重みを調整することで勝者のニューロンを支持していることを明確に示しています。ニューロンが失われた場合は、わざわざその重みを再調整する必要はありません。