離散数学-群論
セミグループ
二項演算$ '\ omicron' $(合成)を持つ有限または無限集合$ 'S' $は、次の2つの条件を同時に保持する場合、半群と呼ばれます-
Closure −すべてのペア$(a、b)\ in Sについて、\ :( a \ omicron b)$は集合$ S $に存在する必要があります。
Associative −すべての要素に対して$ a、b、c \ in S、(a \ omicron b)\ omicron c = a \ omicron(b \ omicron c)$が成立する必要があります。
例
加算演算を伴う正の整数(ゼロを除く)のセットは半群です。たとえば、$ S = \ lbrace 1、2、3、\ dots \ rbrace $
ここで、閉閉性はすべてのペアについて保持されます$(a、b)\ in S、(a + b)$は集合Sに存在します。たとえば、$ 1 + 2 = 3 \ in S] $
結合法則は、すべての要素$ a、b、c \ in S、(a + b)+ c = a +(b + c)$にも当てはまります。たとえば、$(1 + 2)+ 3 = 1 +(2 + 3)= 5 $
モノイド
モノイドは、単位元を持つ半群です。セットSの単位元($ e $またはEで示される)は、すべての要素$ a \ in S $に対して、$(a \ omicron e)= a $となる要素です。単位元は、unit element。したがって、モノイドは3つのプロパティを同時に保持します-Closure, Associative, Identity element。
例
乗算演算を使用した正の整数(ゼロを除く)のセットはモノイドです。$ S = \ lbrace 1、2、3、\ dots \ rbrace $
ここで、閉性プロパティは、すべてのペア$(a、b)\ in Sについて保持され、(a \ times b)$は集合Sに存在します。[たとえば、$ 1 \ times 2 = 2 \ in S $など]
結合法則は、すべての要素に対しても保持されます$ a、b、c \ in S、(a \ times b)\ times c = a \ times(b \ times c)$ [たとえば、$(1 \ times 2)\ times 3 = 1 \ times(2 \ times 3)= 6 $など]
単位元プロパティは、すべての要素$ a \ in S、(a \ times e)= a $ [たとえば、$(2 \ times 1)= 2、(3 \ times 1)= 3 $など]にも適用されます。ここで、単位元は1です。
グループ
グループは、逆元を持つモノイドです。セットSの逆元(Iで示される)は、各要素$ a \ in S $に対して、$(a \ omicron I)=(I \ omicron a)= a $のような要素です。したがって、グループは4つのプロパティを同時に保持します-i)クロージャー、ii)連想、iii)単位元、iv)逆元。グループGの位数は、G内の要素の数であり、グループ内の要素の位数は、anがそのグループGの単位元であるような最小の正の整数nです。
例
$ N \ times N $の非特異行列のセットは、行列乗算演算の下でグループを形成します。
2つの$ N \ times N $非特異行列の積も、閉包特性を保持する$ N \ times N $非特異行列です。
行列の乗算自体は結合法則です。したがって、結合法則が成り立ちます。
$ N \ times N $非特異行列のセットには、単位元プロパティを保持する単位行列が含まれています。
すべての行列は非特異であるため、それらはすべて非特異行列でもある逆元を持っています。したがって、逆特性も成り立ちます。
アーベル群
アーベル群Gは、要素ペア$(a、b)\ in G $が常に可換法則を保持する群です。したがって、グループは5つのプロパティを同時に保持します-i)クロージャー、ii)連想、iii)単位元、iv)逆元、v)可換。
例
加算演算を伴う正の整数(ゼロを含む)のセットは、アーベル群です。$ G = \ lbrace 0、1、2、3、\ dots \ rbrace $
ここで、閉性プロパティは、すべてのペア$(a、b)\ in Sについて保持され、(a + b)$は集合Sに存在します。[たとえば、$ 1 + 2 = 2 \ in S $など]
結合法則は、すべての要素$ a、b、c \ in S、(a + b)+ c = a +(b + c)$ [たとえば、$(1 +2)+ 3 = 1 +(2 + 3)= 6 $など]
単位元プロパティは、すべての要素$ a \ in S、(a \ times e)= a $ [たとえば、$(2 \ times 1)= 2、(3 \ times 1)= 3 $など]にも適用されます。ここで、単位元は1です。
可換性はすべての要素に対しても成り立ちます$ a \ in S、(a \ times b)=(b \ times a)$ [たとえば、$(2 \ times 3)=(3 \ times 2)= 3 $などオン]
巡回群とサブグループ
A cyclic groupは、単一の要素で生成できるグループです。巡回群のすべての要素は、ジェネレーターと呼ばれる特定の要素の累乗です。巡回群はジェネレーター 'g'によって生成でき、グループの他のすべての要素はジェネレーター 'g'の累乗として記述できます。
例
乗算演算中の複素数$ \ lbrace 1、-1、i、-i \ rbrace $のセットは巡回群です。
$ i ^ 1 = i、i ^ 2 = -1、i ^ 3 = -i、i ^ 4 = 1 $、および$(– i)^ 1として、2つのジェネレーター-$ i $と$ –i $があります。 = -i、(– i)^ 2 = -1、(– i)^ 3 = i、(– i)^ 4 = 1 $これは、グループのすべての要素をカバーします。したがって、それは巡回群です。
Note − a cyclic groupは常にアーベル群ですが、すべてのアーベル群が巡回群であるとは限りません。加算中の有理数は巡回ではありませんが、アーベルです。
A subgroup Hは、4つの特性を同時に満たす場合、グループGのサブセット($H≤G$で示される)です。 Closure, Associative, Identity element、および Inverse。
グループG全体を含まないグループGのサブグループHは、適切なサブグループと呼ばれます($ H <G $で示されます)。巡回群のサブグループは巡回であり、アーベル群もアーベルです。
例
グループ$ G = \ lbrace 1、i、-1、-i \ rbrace $とします。
次に、いくつかのサブグループは$ H_1 = \ lbrace 1 \ rbrace、H_2 = \ lbrace 1、-1 \ rbrace $、
これはサブグループではありません-$(i)^ {-1} = -i $が$ H_3 $にないため、$ H_3 = \ lbrace 1、i \ rbrace $
半順序集合(POSET)
半順序集合は、反射的、反対称的、推移的である二項関係を持つ集合で構成されます。「半順序集合」はPOSETと略されます。
例
$(\ le)$以下の二項演算での実数のセットは半順序集合です。
集合$ S = \ lbrace 1、2、3 \ rbrace $とし、操作は$ \ le $です。
関係は$ \ lbrace(1、1)、(2、2)、(3、3)、(1、2)、(1、3)、(2、3)\ rbrace $になります
この関係Rは、$ \ lbrace(1、1)、(2、2)、(3、3)\ rbrace \ in R $のように反射的です。
この関係Rは、次のように反対称です。
$ \ lbrace(1、2)、(1、3)、(2、3)\ rbrace \ in R \および\\ lbrace(1、2)、(1、3)、(2、3)\rbrace∉ R $
この関係Rは、$ \ lbrace(1,2)、(2,3)、(1,3)\ rbrace \ in R $としても推移的です。
したがって、それは poset。
演算「到達可能性」の下での有向非巡回グラフの頂点セットは半順序集合です。
ハッセ図
ポセットのハッセ図は、頂点がそのポセットの要素であり、円弧がポセットのペア(x、y)をカバーする有向グラフです。半順序集合$ x <y $の場合、点xはハッセ図の点yよりも低く表示されます。ポセットで$ x <y <z $の場合、矢印は暗黙的であるため、xとzの間に表示されません。
例
$ \ lbrace 1、2、3 \ rbrace = \ lbrace \ emptyset、\ lbrace 1 \ rbrace、\ lbrace 2 \ rbrace、\ lbrace 3 \ rbrace、\ lbrace 1、2 \ rbrace、\ lbrace1のサブセットのポセット、3 \ rbrace、\ lbrace 2、3 \ rbrace、\ lbrace 1、2、3 \ rbrace \ rbrace $は、次のハッセ図で示されます。
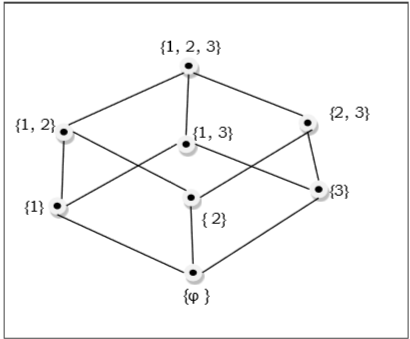
線形順序のセット
線形順序セットまたは全順序セットは、要素のすべてのペアが比較可能な半順序セットです。$ a \ le b $または$ b \ le a $のいずれかが成り立つ場合、要素$ a、b \ in S $は同等であると言われます。三分法は、この順序集合の合計を定義します。全順序集合は、集合Sのaとbのすべての値に対してプロパティ$ \ lbrace a \ lor b、\ land b \ rbrace = \ lbrace a、b \ rbrace $を持つ分配束として定義できます。
例
\ subseteqによって順序付けられた$ \ lbrace a、b \ rbrace $のべき集合は、べき集合$ P = \ lbrace \ emptyset、\ lbrace a \ rbrace、\ lbrace b \ rbrace、\のすべての要素として完全に順序付けられたセットです。 lbrace a、b \ rbrace \ rbrace $は同等です。
非合計注文セットの例
操作xがyを除算するセット$ S = \ lbrace 1、2、3、4、5、6 \ rbrace $は、順序集合の合計ではありません。
ここで、すべての$(x、y)\ in S、x | y $は保持する必要がありますが、2 | 3、2は3を分割しないか、3は2を分割しないため、これは完全な順序集合ではありません。
格子
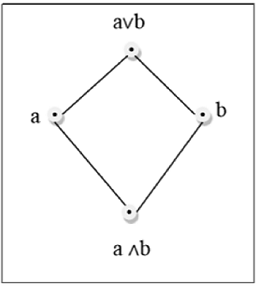
ラティスは、すべてのペア$ \ lbrace a、b \ rbrace \ in L $が最小の上限($ a \ lor b $で示される)と最大の下限($ a \ lor b $で示される)を持つ半順序集合$(L、\ le)$です。 $ a \ land b $で示されます)。LUB $(\ lbrace a、b \ rbrace)$は、aとbの結合と呼ばれます。GLB $(\ lbrace a、b \ rbrace)$は、aとbの出会いと呼ばれます。
例
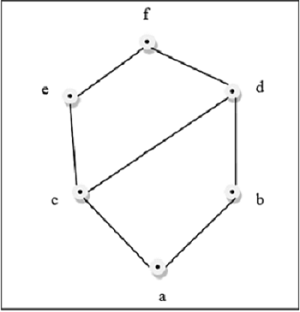
この上の図は、すべてのペア$ \ lbrace a、b \ rbrace \ in L $に対して、GLBとLUBが存在するため、格子です。
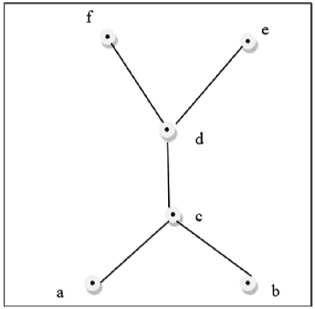
$ GLB(a、b)$と$ LUB(e、f)$が存在しないため、この上の図は格子ではありません。
他のいくつかのラティスについて以下で説明します-
有界格子
格子Lは、最大要素1と最小要素0がある場合、有界格子になります。
可補束
格子Lは、それが有界格子であり、格子内のすべての要素が補集合を持っている場合、可補束になります。$ \ exists x(x \ land x '= 0およびx \ lor x' = 1)$の場合、要素xには補数x 'があります
分配束
格子が次の2つの分配特性を満たす場合、それは分配束と呼ばれます。
$ a \ lor(b \ land c)=(a \ lor b)\ land(a \ lor c)$
$ a \ land(b \ lor c)=(a \ land b)\ lor(a \ land c)$
モジュラー束
格子が次の特性を満たす場合、それはモジュラー格子と呼ばれます。
$ a \ land(b \ lor(a \ land d))=(a \ land b)\ lor(a \ land d)$
格子の性質
べき等プロパティ
$ a \ lor a = a $
$ a \ land a = a $
吸収特性
$ a \ lor(a \ land b)= a $
$ a \ land(a \ lor b)= a $
可換性
$ a \ lor b = b \ lor a $
$ a \ land b = b \ land a $
結合法則
$ a \ lor(b \ lor c)=(a \ lor b)\ lor c $
$ a \ land(b \ land c)=(a \ land b)\ land c $
格子の双対
ラティスの双対は、「$ \ lor $」操作と「$ \ land $」操作を交換することによって取得されます。
例
$ \ lbrack a \ lor(b \ land c)\ rbrack \の双対は\\ lbrack a \ land(b \ lor c)\ rbrack $