離散数学-クイックガイド

数学は大きく2つのカテゴリーに分類できます-

• Continuous Mathematics−連続数直線または実数に基づいています。これは、任意の2つの数値の間に、ほとんどの場合、無限の数値のセットが存在するという事実によって特徴付けられます。たとえば、連続数学の関数は、途切れることなく滑らかな曲線でプロットできます。

• Discrete Mathematics−異なる値が含まれます。つまり、任意の2つのポイントの間に、カウント可能な数のポイントがあります。たとえば、オブジェクトの有限セットがある場合、関数はこれらのオブジェクトを持つ順序対のリストとして定義でき、それらのペアの完全なリストとして表示できます。

離散数学のトピック

離散数学の分岐の数は明確ではありませんが、この問題に関するすべての研究では、ほとんどの場合、次のトピックが取り上げられています。

• セット、関係、関数
• 数理論理学
• 群論
• カウント理論
• Probability
• 数学的帰納法と漸化式
• グラフ理論
• Trees
• ブール代数

これらの各概念については、このチュートリアルの後続の章で説明します。

ドイツの数学者 G. Cantorセットの概念を導入しました。彼は、特定のルールまたは説明によって選択された明確で区別可能なオブジェクトのコレクションとしてセットを定義しました。

Set理論は、カウント理論、関係、グラフ理論、有限状態機械など、他のいくつかの研究分野の基礎を形成します。この章では、のさまざまな側面について説明します。Set Theory。

セット-定義

セットは、さまざまな要素の順序付けられていないコレクションです。セットは、セットブラケットを使用してその要素をリストすることにより、明示的に記述できます。要素の順序が変更されたり、セットのいずれかの要素が繰り返されたりしても、セットは変更されません。

セットのいくつかの例

• すべての正の整数のセット
• 太陽系のすべての惑星のセット
• インドのすべての州のセット
• アルファベットのすべての小文字のセット

セットの表現

セットは2つの方法で表すことができます-

• 名簿または表形式
• 集合の内包的記法

名簿または表形式

セットは、それを構成するすべての要素をリストすることによって表されます。要素は中括弧で囲まれ、コンマで区切られます。

Example 1 −英語のアルファベットの母音のセット、 $A = \lbrace a,e,i,o,u \rbrace$

Example 2 −10未満の奇数のセット $B = \lbrace 1,3,5,7,9 \rbrace$

集合の内包的記法

セットは、セットの要素に共通するプロパティを指定することによって定義されます。セットは次のように説明されています$A = \lbrace x : p(x) \rbrace$

Example 1 −セット $\lbrace a,e,i,o,u \rbrace$ −と書かれています

$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$

Example 2 −セット $\lbrace 1,3,5,7,9 \rbrace$ −と書かれています

$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$

要素xが任意の集合Sのメンバーである場合、それは次のように表されます。 $x \in S$ 要素yが集合Sのメンバーでない場合、次のように表されます。 $y \notin S$。

Example−もし$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ だが $1.5 \notin S$

いくつかの重要なセット

N −すべての自然数の集合= $\lbrace1, 2, 3, 4, .....\rbrace$

Z −すべての整数のセット= $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$

Z⁺ −すべての正の整数のセット

Q −すべての有理数の集合

R −すべての実数のセット

W −すべての整数のセット

セットのカーディナリティ

セットSのカーディナリティ。 $|S|$、はセットの要素の数です。この番号は、基数とも呼ばれます。セットに無限の数の要素がある場合、そのカーディナリティは次のようになります。$\infty$。

Example − $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$

XとYの2つのセットがある場合、

• $|X| = |Y|$同じカーディナリティを持つ2つのセットXとYを示します。Xの要素数がYの要素数と正確に等しい場合に発生します。この場合、XからYへの全単射関数「f」が存在します。

• $|X| \le |Y|$セットXのカーディナリティーがセットYのカーディナリティー以下であることを示します。Xの要素数がYの要素数以下の場合に発生します。ここでは、XからYへの単射関数 'f'が存在します。

• $|X| \lt |Y|$セットXのカーディナリティがセットYのカーディナリティよりも小さいことを示します。Xの要素数がYの要素数より少ない場合に発生します。ここで、XからYへの関数 'f'は単射関数ですが、全単射ではありません。

• $If\ |X| \le |Y|$ そして $|X| \ge |Y|$ その後 $|X| = |Y|$。セットXとYは、一般に同等のセットと呼ばれます。

セットの種類

セットは多くのタイプに分類できます。そのうちのいくつかは、有限、無限、サブセット、ユニバーサル、適切、単集合などです。

有限集合

一定数の要素を含む集合は、有限集合と呼ばれます。

Example − $S = \lbrace x \:| \:x \in N$ そして $70 \gt x \gt 50 \rbrace$

無限セット

無限の数の要素を含むセットは、無限セットと呼ばれます。

Example − $S = \lbrace x \: | \: x \in N $ そして $ x \gt 10 \rbrace$

サブセット

セットXはセットYのサブセットです（ $X \subseteq Y$）Xのすべての要素が集合Yの要素である場合。

Example 1 −みましょう、 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ そして $Y = \lbrace 1, 2 \rbrace$。ここで、セットYのすべての要素がセットXにあるため、セットYはセットXのサブセットです。したがって、次のように記述できます。$Y \subseteq X$。

Example 2 −みましょう、 $X = \lbrace 1, 2, 3 \rbrace$ そして $Y = \lbrace 1, 2, 3 \rbrace$。ここで、セットYのすべての要素がセットXにあるため、セットYはセットXのサブセット（適切なサブセットではありません）です。したがって、次のように記述できます。$Y \subseteq X$。

適切なサブセット

「適切なサブセット」という用語は、「のサブセットであるが等しくない」と定義できます。セットXは、セットYの適切なサブセットです（次のように記述されます）。$ X \subset Y $）Xのすべての要素が集合Yの要素であり、 $|X| \lt |Y|$。

Example −みましょう、 $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ そして $Y = \lbrace 1, 2 \rbrace$。ここに設定$Y \subset X$ のすべての要素が $Y$ に含まれています $X$ あまりにもそして $X$ 少なくとも1つの要素が設定されている以上である $Y$。

ユニバーサルセット

これは、特定のコンテキストまたはアプリケーションのすべての要素のコレクションです。そのコンテキストまたはアプリケーションのすべてのセットは、基本的にこのユニバーサルセットのサブセットです。ユニバーサルセットは次のように表されます$U$。

Example −定義する場合があります $U$地球上のすべての動物のセットとして。この場合、すべての哺乳類のセットはのサブセットです$U$、すべての魚のセットはのサブセットです $U$、すべての昆虫のセットはのサブセットです $U$、 等々。

空のセットまたはヌルセット

空のセットには要素が含まれていません。それはによって示されます$\emptyset$。空集合の要素数は有限であるため、空集合は有限集合です。空集合または零集合のカーディナリティはゼロです。

Example − $S = \lbrace x \:| \: x \in N$ そして $7 \lt x \lt 8 \rbrace = \emptyset$

シングルトンセットまたはユニットセット

シングルトンセットまたはユニットセットには、要素が1つだけ含まれています。単集合はで表されます$\lbrace s \rbrace$。

Example − $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$

等しいセット

2つのセットに同じ要素が含まれている場合、それらは等しいと言われます。

Example −もし $A = \lbrace 1, 2, 6 \rbrace$ そして $B = \lbrace 6, 1, 2 \rbrace$、セットAのすべての要素がセットBの要素であり、セットBのすべての要素がセットAの要素であるため、これらは等しくなります。

同等のセット

2つのセットのカーディナリティが同じである場合、それらは同等のセットと呼ばれます。

Example −もし $A = \lbrace 1, 2, 6 \rbrace$ そして $B = \lbrace 16, 17, 22 \rbrace$、AのカーディナリティはBのカーディナリティに等しいため、これらは同等です。 $|A| = |B| = 3$

重複セット

少なくとも1つの共通要素を持つ2つのセットは、オーバーラップセットと呼ばれます。

セットが重複している場合-

• $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

• $n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$

• $n(A) = n(A - B) + n(A \cap B)$

• $n(B) = n(B - A) + n(A \cap B)$

Example −みましょう、 $A = \lbrace 1, 2, 6 \rbrace$ そして $B = \lbrace 6, 12, 42 \rbrace$。共通の要素「6」があるため、これらのセットは重複するセットです。

素集合

2つのセットAとBは、共通の要素が1つもない場合、互いに素なセットと呼ばれます。したがって、互いに素な集合には次の特性があります。

• $n(A \cap B) = \emptyset$

• $n(A \cup B) = n(A) + n(B)$

Example −みましょう、 $A = \lbrace 1, 2, 6 \rbrace$ そして $B = \lbrace 7, 9, 14 \rbrace$、単一の共通要素がないため、これらのセットは重複するセットです。

ベン図

1880年にジョンベンによって発明されたベン図は、さまざまな数学的セット間のすべての可能な論理関係を示す概略図です。

Examples

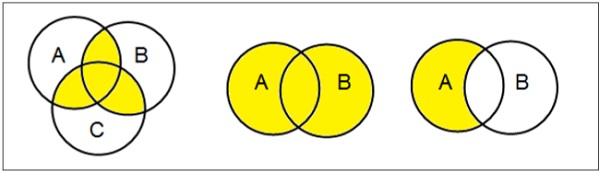
セット操作

セット操作には、セットユニオン、セット交差、セット差、セットの補集合、および直積が含まれます。

セットユニオン

セットAとBの和集合（ $A \cup B$）は、A、B、またはAとBの両方にある要素のセットです。したがって、 $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$。

Example −もし $A = \lbrace 10, 11, 12, 13 \rbrace$ およびB = $\lbrace 13, 14, 15 \rbrace$、その後 $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。（共通要素は1回だけ発生します）

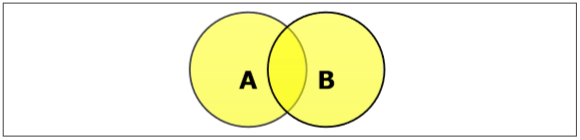
交差点を設定

セットAとBの共通部分（で示される） $A \cap B$）は、AとBの両方にある要素のセットです。したがって、 $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$。

Example −もし $A = \lbrace 11, 12, 13 \rbrace$ そして $B = \lbrace 13, 14, 15 \rbrace$、その後 $A \cap B = \lbrace 13 \rbrace$。

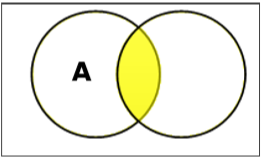
差/相対補数を設定します

セットAとセットBのセット差（で示される） $A – B$）は、Aにのみ存在し、Bには存在しない要素のセットです。したがって、 $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$。

Example −もし $A = \lbrace 10, 11, 12, 13 \rbrace$ そして $B = \lbrace 13, 14, 15 \rbrace$、その後 $(A - B) = \lbrace 10, 11, 12 \rbrace$ そして $(B - A) = \lbrace 14, 15 \rbrace$。ここで、私たちは見ることができます$(A - B) \ne (B - A)$

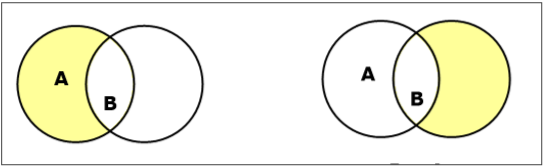
セットの補集合

セットAの補集合（で示される） $A’$）は、セットAにない要素のセットです。したがって、 $A' = \lbrace x | x \notin A \rbrace$。

すなわち、 $A'= (U - A)$ どこ $U$ すべてのオブジェクトを含むユニバーサルセットです。

Example −もし $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ その後 $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$

デカルト積/クロス積

n個のセットのデカルト積 $A_1, A_2, \dots A_n$ として示される $A_1 \times A_2 \dots \times A_n$ 可能なすべての順序対として定義できます $(x_1, x_2, \dots x_n)$ どこ $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$

Example −2セット取ったら $A = \lbrace a, b \rbrace$ そして $B = \lbrace 1, 2 \rbrace$、

AとBのデカルト積は次のように記述されます- $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$

BとAのデカルト積は次のように記述されます- $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$

パワーセット

セットSのべき集合は、空のセットを含むSのすべてのサブセットのセットです。カーディナリティnのセットSのべき集合のカーディナリティは$2^n$。べき集合は次のように表されます$P(S)$。

Example −

セットの場合 $S = \lbrace a, b, c, d \rbrace$ サブセットを計算してみましょう-

• 要素が0のサブセット- $\lbrace \emptyset \rbrace$ （空のセット）

• 1つの要素を持つサブセット- $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$

• 2つの要素を持つサブセット- $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$

• 3つの要素を持つサブセット- $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$

• 4つの要素を持つサブセット- $\lbrace a, b, c, d \rbrace$

したがって、 $P(S)=$

$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$

$| P(S) | = 2^4 = 16$

Note −空のセットのべき集合も空のセットです。

$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$

セットの分割

セットの分割、たとえばSは、n個の互いに素なサブセットのコレクションです。$P_1, P_2, \dots P_n$ 次の3つの条件を満たす-

• $P_i$ 空のセットは含まれていません。

  $\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$

• サブセットの和集合は、元のセット全体と等しくなければなりません。

  $\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$

• 2つの異なるセットの共通部分は空です。

  $\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$

Example

しましょう $S = \lbrace a, b, c, d, e, f, g, h \rbrace$

考えられるパーティショニングの1つは $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$

別の可能性のあるパーティショニングは $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$

ベル数

ベル数は、セットを分割する方法の数を示します。それらはによって示されます$B_n$ ここで、nはセットのカーディナリティです。

Example −

しましょう $S = \lbrace 1, 2, 3\rbrace$、 $n = |S| = 3$

代替パーティションは-

1.1。 $\emptyset , \lbrace 1, 2, 3 \rbrace$

2.2。 $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$

3.3。 $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$

4.4。 $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$

5.5。 $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$

したがって、 $B_3 = 5$

セットが議論されているときはいつでも、セットの要素間の関係が次に浮かび上がります。 Relations 同じセットのオブジェクト間、または2つ以上のセットのオブジェクト間に存在する場合があります。

定義とプロパティ

セットxからyへの二項関係R（ $xRy$ または $R(x,y)$）はデカルト積のサブセットです $x \times y$。Gの順序対が逆になると、関係も変化します。

一般に、集合間のn項関係R $A_1, \dots ,\ and\ A_n$ n項積のサブセットです $A_1 \times \dots \times A_n$。関係Rの最小カーディナリティはゼロで、最大はゼロです。$n^2$ この場合。

単一の集合A上の二項関係Rは、 $A \times A$。

それぞれカーディナリティmとnを持つ2つの異なるセットAとBの場合、AからBへの関係Rの最大カーディナリティはmnです。

ドメインと範囲

2つのセットAとBがあり、関係Rの順序対（x、y）がある場合、-

• ザ・ domain RのDom（R）がセットです $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$

• ザ・ range RのRan（R）はセットです $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$

例

しましょう、 $A = \lbrace 1, 2, 9 \rbrace $ そして $ B = \lbrace 1, 3, 7 \rbrace$

• ケース1-関係Rが「等しい」の場合 $R = \lbrace (1, 1), (3, 3) \rbrace$

  Dom（R）= $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$

• ケース2-関係Rが「より小さい」の場合 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$

  Dom（R）= $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$

• ケース3-関係Rが「より大きい」の場合 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$

  Dom（R）= $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$

グラフを使用した関係の表現

関係は、有向グラフを使用して表すことができます。

グラフ内の頂点の数は、リレーションが定義されているセット内の要素の数と同じです。関係Rの順序対（x、y）ごとに、頂点 'x'から頂点 'y'への有向エッジがあります。順序対（x、x）がある場合、頂点 'x'に自己ループがあります。

関係があるとしましょう $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ セットで $S = \lbrace 1, 2, 3 \rbrace$、次のグラフで表すことができます-

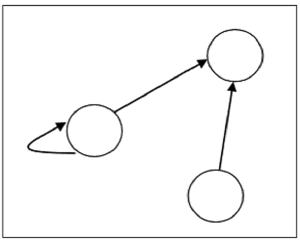
関係の種類

• ザ・ Empty Relation セットXとYの間、またはEでは、空のセットです。 $\emptyset$

• ザ・ Full Relation セットXとYの間はセットです $X \times Y$

• ザ・ Identity Relation セットXはセットです $\lbrace (x, x) | x \in X \rbrace$

• 関係Rの逆関係R 'は次のように定義されます。 $R' = \lbrace (b, a) | (a, b) \in R \rbrace$

  Example −もし $R = \lbrace (1, 2), (2, 3) \rbrace$ その後 $R' $ になります $\lbrace (2, 1), (3, 2) \rbrace$

• セットAの関係Rはと呼ばれます Reflexive もし $\forall a \in A$ （aRaホールド）に関連しています

  Example −関係 $R = \lbrace (a, a), (b, b) \rbrace$ セットで $X = \lbrace a, b \rbrace$ 反射的です。

• セットAの関係Rはと呼ばれます Irreflexive いいえの場合 $a \in A$ に関連しています（aRaは保持されません）。

  Example −関係 $R = \lbrace (a, b), (b, a) \rbrace$ セットで $X = \lbrace a, b \rbrace$ 反射的ではありません。

• セットAの関係Rはと呼ばれます Symmetric もし $xRy$ 意味する $yRx$、 $\forall x \in A$ そして $\forall y \in A$。

  Example −関係 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ セットで $A = \lbrace 1, 2, 3 \rbrace$ 対称です。

• セットAの関係Rはと呼ばれます Anti-Symmetric もし $xRy$ そして $yRx$ 意味する $x = y \: \forall x \in A$ そして $\forall y \in A$。

  Example −関係 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 反対称です $x \leq y$ そして $y \leq x$ 意味する $x = y$。

• セットAの関係Rはと呼ばれます Transitive もし $xRy$ そして $yRz$ 意味する $xRz, \forall x,y,z \in A$。

  Example −関係 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ セットで $A = \lbrace 1, 2, 3 \rbrace$ 推移的です。

• 関係は Equivalence Relation それが反射的、対称的、推移的である場合。

  Example −関係 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ セットで $A = \lbrace 1, 2, 3 \rbrace$ は、反射的、対称的、推移的であるため、同値関係です。

A Functionセットの各要素に、関連するセットの1つの要素だけを割り当てます。関数は、アルゴリズムの計算の複雑さの表現、オブジェクトのカウント、シーケンスと文字列の研究など、さまざまな分野でアプリケーションを見つけます。このパートの第3章と最後の章では、関数の重要な側面に焦点を当てています。

機能-定義

関数またはマッピング（として定義 $f: X \rightarrow Y$）は、あるセットXの要素から別のセットYの要素への関係です（XとYは空でないセットです）。Xは定義域と呼ばれ、Yは関数「f」の終域と呼ばれます。

関数 'f'は、XとYの関係であり、 $x \in X$、ユニークな存在があります $y \in Y$ そのような $(x,y) \in R$。「x」はプレイメージと呼ばれ、「y」は関数fのイメージと呼ばれます。

関数は、1対1または多対1にすることができますが、1対多にすることはできません。

単射/ 1対1の機能

機能 $f: A \rightarrow B$ すべての場合、単射または1対1の機能です $b \in B$、最大で1つ存在します $a \in A$ そのような $f(s) = t$。

これは機能を意味します f 次の場合は単射です $a_1 \ne a_2$ 意味する $f(a1) \ne f(a2)$。

例

• $f: N \rightarrow N, f(x) = 5x$ 単射です。

• $f: N \rightarrow N, f(x) = x^2$ 単射です。

• $f: R\rightarrow R, f(x) = x^2$ として単射ではありません $(-x)^2 = x^2$

全射/全射

機能 $f: A \rightarrow B$fの画像がその範囲に等しい場合、は全射です。同等に、すべての$b \in B$、いくつかあります $a \in A$ そのような $f(a) = b$。これは、Bの任意のyに対して、Aに次のようなxが存在することを意味します。$y = f(x)$。

例

• $f : N \rightarrow N, f(x) = x + 2$ 全射です。

• $f : R \rightarrow R, f(x) = x^2$ 二乗が負の実数を見つけることができないため、全射ではありません。

全単射/ 1対1の特派員

機能 $f: A \rightarrow B$ 単射または1対1の特派員であるのは、 f 単射と全射の両方です。

問題

その機能を証明する $f: R \rightarrow R$ によって定義されます $f(x) = 2x – 3$ 全単射関数です。

Explanation −この関数が単射と全射の両方であることを証明する必要があります。

場合 $f(x_1) = f(x_2)$、その後 $2x_1 – 3 = 2x_2 – 3 $ そしてそれはそれを意味します $x_1 = x_2$。

したがって、fは injective。

ここに、 $2x – 3= y$

そう、 $x = (y+5)/3$ Rに属し、 $f(x) = y$。

したがって、fは surjective。

以来 f 両方 surjective そして injective、 と言えます f です bijective。

関数の逆関数

ザ・ inverse 1対1の対応する関数の $f : A \rightarrow B$、は関数です $g : B \rightarrow A$、次のプロパティを保持します-

$f(x) = y \Leftrightarrow g(y) = x$

関数fが呼び出されます invertible、その逆関数gが存在する場合。

例

• 機能 $f : Z \rightarrow Z, f(x)=x+5$、は逆関数を持っているので反転可能です $ g : Z \rightarrow Z, g(x)= x-5$。

• 機能 $f : Z \rightarrow Z, f(x)=x^2$ これは1対1ではないため、反転できません。 $(-x)^2=x^2$。

機能の構成

2つの機能 $f: A \rightarrow B$ そして $g: B \rightarrow C$ 構成を与えるために構成することができます $g o f$。これは、によって定義されるAからCまでの関数です。$(gof)(x) = g(f(x))$

例

しましょう $f(x) = x + 2$ そして $g(x) = 2x + 1$、検索 $( f o g)(x)$ そして $( g o f)(x)$。

解決

$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$

$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$

したがって、 $(f o g)(x) \neq (g o f)(x)$

構成に関するいくつかの事実

• fとgが1対1の場合、関数 $(g o f)$ また、1対1です。

• fとgが上にある場合、関数 $(g o f)$ にもあります。

• 合成は常に結合法則を保持しますが、可換性は保持しません。

数理論理学の規則は、数学的ステートメントを推論する方法を指定します。ギリシャの哲学者、アリストテレスは論理的推論の先駆者でした。論理的推論は、数学、ひいてはコンピュータサイエンスの多くの分野の理論的基盤を提供します。コンピューティングマシンの設計、人工知能、プログラミング言語のデータ構造の定義など、コンピュータサイエンスで多くの実用的なアプリケーションがあります。

Propositional Logicは、真理値「true」および「false」を割り当てることができるステートメントに関係しています。目的は、これらのステートメントを個別に、または複合的に分析することです。

命題論理–定義

命題は、真理値「true」または真理値「false」のいずれかを持つ宣言型ステートメントのコレクションです。命題は、命題変数と結合要素で構成されます。命題変数は大文字（A、Bなど）で示されます。結合は命題変数を接続します。

命題のいくつかの例を以下に示します-

• 「ManisMortal」、真理値「TRUE」を返します
• 「12+ 9 = 3 – 2」、真理値「FALSE」を返します

以下は提案ではありません-

• 「Aは2未満です」。これは、Aの特定の値を指定しない限り、ステートメントが真であるか偽であるかを判断できないためです。

接続詞

命題論理では、一般に、次の5つの連結語を使用します。

• または（$\lor$）

• AND（$\land$）

• 否定/ NOT（$\lnot$）

• 含意/ if-then（$\rightarrow$）

• 場合に限り（$\Leftrightarrow$）。

OR ($\lor$) − 2つの命題AとBのOR演算（次のように記述） $A \lor B$）命題変数AまたはBの少なくともいずれかが真である場合、真です。

真理値表は次のとおりです-

A	B	A∨B
本当	本当	本当
本当	誤り	本当
誤り	本当	本当
誤り	誤り	誤り

AND ($\land$) − 2つの命題AとBのAND演算（次のように記述） $A \land B$）命題変数AとBの両方が真の場合は真です。

真理値表は次のとおりです-

A	B	A∧B
本当	本当	本当
本当	誤り	誤り
誤り	本当	誤り
誤り	誤り	誤り

Negation ($\lnot$) −命題Aの否定（ $\lnot A$）Aが真の場合は偽、Aが偽の場合は真。

真理値表は次のとおりです-

A	¬A
本当	誤り
誤り	本当

Implication / if-then ($\rightarrow$) −含意 $A \rightarrow B$「もしAならB」という命題です。Aが真でBが偽の場合は偽です。残りのケースは本当です。

真理値表は次のとおりです-

A	B	A→B
本当	本当	本当
本当	誤り	誤り
誤り	本当	本当
誤り	誤り	本当

If and only if ($ \Leftrightarrow $) − $A \Leftrightarrow B$ は双条件論理積であり、pとqが同じ場合、つまり両方が偽であるか、両方が真である場合に真になります。

真理値表は次のとおりです-

A	B	A⇔B
本当	本当	本当
本当	誤り	誤り
誤り	本当	誤り
誤り	誤り	本当

トートロジー

トートロジーは、命題変数のすべての値に常に当てはまる公式です。

Example −証明する $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ トートロジーです

真理値表は次のとおりです-

A	B	A→B	（A→B）∧A	[（A→B）∧A]→B
本当	本当	本当	本当	本当
本当	誤り	誤り	誤り	本当
誤り	本当	本当	誤り	本当
誤り	誤り	本当	誤り	本当

私たちが見ることができるように $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 「真」であり、トートロジーです。

矛盾

矛盾は、命題変数のすべての値に対して常に偽である式です。

Example −証明する $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 矛盾です

真理値表は次のとおりです-

A	B	A∨B	¬A	¬B	（¬A）∧（¬B）	（A∨B）∧[（¬A）∧（¬B）]
本当	本当	本当	誤り	誤り	誤り	誤り
本当	誤り	本当	誤り	本当	誤り	誤り
誤り	本当	本当	本当	誤り	誤り	誤り
誤り	誤り	誤り	本当	本当	本当	誤り

私たちが見ることができるように $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 「False」です、それは矛盾です。

不測の事態

偶然性は、命題変数のすべての値に対していくつかの真の値といくつかの偽の値の両方を持つ式です。

Example −証明する $(A \lor B) \land (\lnot A)$ 不測の事態

真理値表は次のとおりです-

A	B	A∨B	¬A	（A∨B）∧（¬A）
本当	本当	本当	誤り	誤り
本当	誤り	本当	誤り	誤り
誤り	本当	本当	本当	本当
誤り	誤り	誤り	本当	誤り

私たちが見ることができるように $(A \lor B) \land (\lnot A)$ 「True」と「False」の両方があり、それは不測の事態です。

提案的等価性

次の2つの条件のいずれかが当てはまる場合、2つのステートメントXとYは論理的に等価です。

• 各ステートメントの真理値表は同じ真理値を持っています。

• 双条件ステートメント $X \Leftrightarrow Y$ トートロジーです。

Example −証明する $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ 同等です

1^番目の方法によるテスト（真理値表のマッチング）

A	B	A∨B	¬（A∨B）	¬A	¬B	[（¬A）∧（¬B）]
本当	本当	本当	誤り	誤り	誤り	誤り
本当	誤り	本当	誤り	誤り	本当	誤り
誤り	本当	本当	誤り	本当	誤り	誤り
誤り	誤り	False	True	True	True	True

Here, we can see the truth values of $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ are same, hence the statements are equivalent.

Testing by 2^nd method (Bi-conditionality)

A	B	¬ (A ∨ B )	[(¬ A) ∧ (¬ B)]	[¬ (A ∨ B)] ⇔ [(¬ A ) ∧ (¬ B)]
True	True	False	False	True
True	False	False	False	True
False	True	False	False	True
False	False	True	True	True

As $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ is a tautology, the statements are equivalent.

Inverse, Converse, and Contra-positive

Implication / if-then $(\rightarrow)$ is also called a conditional statement. It has two parts −

• Hypothesis, p
• Conclusion, q

As mentioned earlier, it is denoted as $p \rightarrow q$.

Example of Conditional Statement − “If you do your homework, you will not be punished.” Here, "you do your homework" is the hypothesis, p, and "you will not be punished" is the conclusion, q.

Inverse − An inverse of the conditional statement is the negation of both the hypothesis and the conclusion. If the statement is “If p, then q”, the inverse will be “If not p, then not q”. Thus the inverse of $p \rightarrow q$ is $ \lnot p \rightarrow \lnot q$.

Example − The inverse of “If you do your homework, you will not be punished” is “If you do not do your homework, you will be punished.”

Converse − The converse of the conditional statement is computed by interchanging the hypothesis and the conclusion. If the statement is “If p, then q”, the converse will be “If q, then p”. The converse of $p \rightarrow q$ is $q \rightarrow p$.

Example − The converse of "If you do your homework, you will not be punished" is "If you will not be punished, you do your homework”.

Contra-positive − The contra-positive of the conditional is computed by interchanging the hypothesis and the conclusion of the inverse statement. If the statement is “If p, then q”, the contra-positive will be “If not q, then not p”. The contra-positive of $p \rightarrow q$ is $\lnot q \rightarrow \lnot p$.

Example − The Contra-positive of " If you do your homework, you will not be punished” is "If you are punished, you did not do your homework”.

Duality Principle

Duality principle states that for any true statement, the dual statement obtained by interchanging unions into intersections (and vice versa) and interchanging Universal set into Null set (and vice versa) is also true. If dual of any statement is the statement itself, it is said self-dual statement.

Example − The dual of $(A \cap B ) \cup C$ is $(A \cup B) \cap C$

Normal Forms

We can convert any proposition in two normal forms −

• Conjunctive normal form
• Disjunctive normal form

Conjunctive Normal Form

A compound statement is in conjunctive normal form if it is obtained by operating AND among variables (negation of variables included) connected with ORs. In terms of set operations, it is a compound statement obtained by Intersection among variables connected with Unions.

Examples

• $(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$

• $(P \cup Q) \cap (Q \cup R)$

Disjunctive Normal Form

A compound statement is in disjunctive normal form if it is obtained by operating OR among variables (negation of variables included) connected with ANDs. In terms of set operations, it is a compound statement obtained by Union among variables connected with Intersections.

Examples

• $(A \land B) \lor (A \land C) \lor (B \land C \land D)$

• $(P \cap Q) \cup (Q \cap R)$

Predicate Logic deals with predicates, which are propositions containing variables.

Predicate Logic – Definition

A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can be made a proposition by either assigning a value to the variable or by quantifying the variable.

The following are some examples of predicates −

• Let E(x, y) denote "x = y"
• Let X(a, b, c) denote "a + b + c = 0"
• Let M(x, y) denote "x is married to y"

Well Formed Formula

Well Formed Formula (wff) is a predicate holding any of the following −

• All propositional constants and propositional variables are wffs

• If x is a variable and Y is a wff, $\forall x Y$ and $\exists x Y$ are also wff

• Truth value and false values are wffs

• Each atomic formula is a wff

• All connectives connecting wffs are wffs

Quantifiers

The variable of predicates is quantified by quantifiers. There are two types of quantifier in predicate logic − Universal Quantifier and Existential Quantifier.

Universal Quantifier

Universal quantifier states that the statements within its scope are true for every value of the specific variable. It is denoted by the symbol $\forall$.

$\forall x P(x)$ is read as for every value of x, P(x) is true.

Example − "Man is mortal" can be transformed into the propositional form $\forall x P(x)$ where P(x) is the predicate which denotes x is mortal and the universe of discourse is all men.

Existential Quantifier

Existential quantifier states that the statements within its scope are true for some values of the specific variable. It is denoted by the symbol $\exists $.

$\exists x P(x)$ is read as for some values of x, P(x) is true.

Example − "Some people are dishonest" can be transformed into the propositional form $\exists x P(x)$ where P(x) is the predicate which denotes x is dishonest and the universe of discourse is some people.

Nested Quantifiers

If we use a quantifier that appears within the scope of another quantifier, it is called nested quantifier.

Example

• $\forall\ a\: \exists b\: P (x, y)$ where $P (a, b)$ denotes $a + b = 0$

• $\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ where $P (a, b)$ denotes $a + (b + c) = (a + b) + c$

Note − $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$

To deduce new statements from the statements whose truth that we already know, Rules of Inference are used.

What are Rules of Inference for?

Mathematical logic is often used for logical proofs. Proofs are valid arguments that determine the truth values of mathematical statements.

An argument is a sequence of statements. The last statement is the conclusion and all its preceding statements are called premises (or hypothesis). The symbol “$\therefore$”, (read therefore) is placed before the conclusion. A valid argument is one where the conclusion follows from the truth values of the premises.

Rules of Inference provide the templates or guidelines for constructing valid arguments from the statements that we already have.

Table of Rules of Inference

Rule of Inference	Name	Rule of Inference	Name
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$	Addition	$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$	Disjunctive Syllogism
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$	Conjunction	$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$	Hypothetical Syllogism
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$	Simplification	$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$	Constructive Dilemma
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$	Modus Ponens	$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$	Destructive Dilemma
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$	Modus Tollens

Addition

If P is a premise, we can use Addition rule to derive $ P \lor Q $.

$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$

Example

Let P be the proposition, “He studies very hard” is true

Therefore − "Either he studies very hard Or he is a very bad student." Here Q is the proposition “he is a very bad student”.

Conjunction

If P and Q are two premises, we can use Conjunction rule to derive $ P \land Q $.

$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$

Example

Let P − “He studies very hard”

Let Q − “He is the best boy in the class”

Therefore − "He studies very hard and he is the best boy in the class"

Simplification

If $P \land Q$ is a premise, we can use Simplification rule to derive P.

$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$

Example

"He studies very hard and he is the best boy in the class", $P \land Q$

Therefore − "He studies very hard"

Modus Ponens

If P and $P \rightarrow Q$ are two premises, we can use Modus Ponens to derive Q.

$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$

Example

"If you have a password, then you can log on to facebook", $P \rightarrow Q$

"You have a password", P

Therefore − "You can log on to facebook"

Modus Tollens

If $P \rightarrow Q$ and $\lnot Q$ are two premises, we can use Modus Tollens to derive $\lnot P$.

$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$

Example

"If you have a password, then you can log on to facebook", $P \rightarrow Q$

"You cannot log on to facebook", $\lnot Q$

Therefore − "You do not have a password "

Disjunctive Syllogism

If $\lnot P$ and $P \lor Q$ are two premises, we can use Disjunctive Syllogism to derive Q.

$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$

Example

"The ice cream is not vanilla flavored", $\lnot P$

"The ice cream is either vanilla flavored or chocolate flavored", $P \lor Q$

Therefore − "The ice cream is chocolate flavored”

Hypothetical Syllogism

If $P \rightarrow Q$ and $Q \rightarrow R$ are two premises, we can use Hypothetical Syllogism to derive $P \rightarrow R$

$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$

Example

"If it rains, I shall not go to school”, $P \rightarrow Q$

"If I don't go to school, I won't need to do homework", $Q \rightarrow R$

Therefore − "If it rains, I won't need to do homework"

Constructive Dilemma

If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.

$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$

Example

“If it rains, I will take a leave”, $( P \rightarrow Q )$

“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$

“Either it will rain or it is hot outside”, $P \lor R$

Therefore − "I will take a leave or I will go for a shower"

Destructive Dilemma

If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.

$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$

Example

“If it rains, I will take a leave”, $(P \rightarrow Q )$

“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$

“Either I will not take a leave or I will not go for a shower”, $\lnot Q \lor \lnot S$

Therefore − "Either it does not rain or it is not hot outside"

Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.

In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −

“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”

In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.

Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.

A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.

The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −

Closure

A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.

Example

Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.

The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.

Associative Laws

A binary operator $\otimes$ on a set A is associative when it holds the following property −

$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $

Example

Let $A = \lbrace 1, 2, 3, 4 \rbrace$

The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.

The operator minus $( - )$ is not associative since

$$( x - y ) - z \ne x - ( y - z )$$

Commutative Laws

A binary operator $\otimes$ on a set A is commutative when it holds the following property −

$x \otimes y = y \otimes x$、 どこ $x, y \in A$

例

しましょう $A = \lbrace 1, 2, 3, 4 \rbrace$

演算子プラス $( + )$ 任意の2つの要素について、可換です。 $x,y \in A$、プロパティ $x + y = y + x$ 保持します。

演算子マイナス $( - )$ 以来、連想的ではありません

$$x - y \ne y - x$$

分配法則

2つの二項演算子 $\otimes$ そして $\circledast$ セットAでは、演算子に対して分配的です $\circledast$ 次のプロパティが成り立つとき−

$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$、 どこ $x, y, z \in A $

例

しましょう $A = \lbrace 1, 2, 3, 4 \rbrace$

に演算子 $( * )$ プラス $( + )$ 任意の3つの要素について、演算子+に対して分配的であるため、 $x,y,z \in A$、プロパティ $x * ( y + z ) = ( x * y ) + ( x * z )$ 保持します。

ただし、これらの演算子は分配的ではありません $*$ 以来

$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$

単位元

セットAには、二項演算に関する単位元があります $\otimes$ Aで、要素が存在する場合 $e \in A$、次のプロパティが成り立つように-

$e \otimes x = x \otimes e$、 どこ $x \in A$

例

しましょう $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

要素1は、操作に関する単位元です。 $*$ どんな要素でも $x \in Z$、

$$1 * x = x * 1$$

一方、マイナス演算の単位元はありません。 $( - )$

逆

セットAに単位元がある場合 $e$ 二項演算子に関して $\otimes $、すべての要素に対して常に逆数があると言われています $x \in A$、別の要素が存在します $y \in A$、次のプロパティが成り立つように-

$$x \otimes y = e$$

例

しましょう $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$

与えられた操作プラス $( + )$ そして $e = 0$、任意の要素xの逆数は $(-x)$ 以来 $x + (x) = 0$

ド・モルガンの法則

ド・モルガンの法則は、補集合の観点から、2つ（またはそれ以上）の集合の和集合と共通部分の間の変換のペアを提供します。法則は-

$$(A \cup B)' = A' \cap B'$$

$$(A \cap B)' = A' \cup B'$$

例

しましょう $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$、および

ユニバーサルセット $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$

$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$

$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$

$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$

$A \cap B = \lbrace 1, 3 \rbrace $

$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$

$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$

したがって、 $(A \cup B)' = A' \cap B'$

$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

したがって、 $(A \cap B)' = A' \cup B'$

セミグループ

有限または無限のセット $‘S’$ 二項演算で $‘\omicron’$ （構成）は、次の2つの条件を同時に保持する場合、半群と呼ばれます-

• Closure −すべてのペアに対して $(a, b) \in S, \:(a \omicron b)$ セットに存在する必要があります $S$。

• Associative −すべての要素について $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ 保持する必要があります。

例

加算演算を伴う正の整数（ゼロを除く）のセットは半群です。例えば、$ S = \lbrace 1, 2, 3, \dots \rbrace $

ここでは、すべてのペアについてクロージャープロパティが保持されます $(a, b) \in S, (a + b)$ セットSに存在します。たとえば、 $1 + 2 = 3 \in S]$

結合法則はすべての要素にも当てはまります $a, b, c \in S, (a + b) + c = a + (b + c)$。例えば、$(1 + 2) + 3 = 1 + (2 + 3) = 5$

モノイド

モノイドは、単位元を持つ半群です。単位元（で示される$e$ またはE）集合Sのは、次のような要素です。 $(a \omicron e) = a$、すべての要素に対して $a \in S$。単位元は、unit element。したがって、モノイドは3つのプロパティを同時に保持します-Closure, Associative, Identity element。

例

乗算演算を使用した正の整数（ゼロを除く）のセットはモノイドです。 $S = \lbrace 1, 2, 3, \dots \rbrace $

ここでは、すべてのペアについてクロージャープロパティが保持されます $(a, b) \in S, (a \times b)$ セットSに存在します。[たとえば、 $1 \times 2 = 2 \in S$ 等々]

結合法則はすべての要素にも当てはまります $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [例えば、 $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ 等々]

単位元プロパティはすべての要素にも適用されます $a \in S, (a \times e) = a$ [例えば、 $(2 \times 1) = 2, (3 \times 1) = 3$等々]。ここで、単位元は1です。

グループ

グループは、逆元を持つモノイドです。集合Sの逆元（Iで示される）は、次のような要素です。$(a \omicron I) = (I \omicron a) = a$、各要素について $a \in S$。したがって、グループは4つのプロパティを同時に保持します-i）クロージャー、ii）連想、iii）単位元、iv）逆元。グループGの位数は、G内の要素の数であり、グループ内の要素の位数は、anがそのグループGの単位元であるような最小の正の整数nです。

例

のセット $N \times N$ 非特異行列は、行列乗算演算の下でグループを形成します。

2つの積 $N \times N$ 非特異行列も $N \times N$ 閉包性を保持する非特異行列。

行列の乗算自体は結合法則です。したがって、結合法則が成り立ちます。

のセット $N \times N$ 非特異行列には、単位元プロパティを保持する単位行列が含まれます。

すべての行列は非特異であるため、それらはすべて非特異行列でもある逆元を持っています。したがって、逆特性も成り立ちます。

アーベル群

アーベル群Gは、要素のペアが含まれる群です。 $(a,b) \in G$常に可換法則を保持します。したがって、グループは5つのプロパティを同時に保持します-i）クロージャー、ii）連想、iii）単位元、iv）逆元、v）可換。

例

加算演算を伴う正の整数（ゼロを含む）のセットは、アーベル群です。 $G = \lbrace 0, 1, 2, 3, \dots \rbrace$

ここでは、すべてのペアについてクロージャープロパティが保持されます $(a, b) \in S, (a + b)$ セットSに存在します。[たとえば、 $1 + 2 = 2 \in S$ 等々]

結合法則はすべての要素にも当てはまります $a, b, c \in S, (a + b) + c = a + (b + c)$ [例えば、 $(1 +2) + 3 = 1 + (2 + 3) = 6$ 等々]

単位元プロパティはすべての要素にも適用されます $a \in S, (a \times e) = a$ [例えば、 $(2 \times 1) = 2, (3 \times 1) = 3$等々]。ここで、単位元は1です。

可換性はすべての要素にも当てはまります $a \in S, (a \times b) = (b \times a)$ [例えば、 $(2 \times 3) = (3 \times 2) = 3$ 等々]

巡回群と部分群

A cyclic groupは、単一の要素で生成できるグループです。巡回群のすべての要素は、ジェネレーターと呼ばれる特定の要素の累乗です。巡回群はジェネレーター「g」によって生成でき、グループの他のすべての要素はジェネレーター「g」の累乗として記述できます。

例

複素数のセット $\lbrace 1,-1, i, -i \rbrace$ 乗算演算の下は巡回群です。

2つのジェネレータがあります- $i$ そして $–i$ なので $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ そしてまた $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$グループのすべての要素をカバーしています。したがって、それは巡回群です。

Note − a cyclic groupは常にアーベル群ですが、すべてのアーベル群が巡回群であるとは限りません。加算中の有理数は巡回ではありませんが、アーベルです。

A subgroup HはグループGのサブセットです（ $H ≤ G$）4つの特性を同時に満たす場合− Closure, Associative, Identity element、および Inverse。

グループG全体を含まないグループGのサブグループHは、適切なサブグループと呼ばれます（ $H < G$）。巡回群のサブグループは巡回であり、アーベル群もアーベルです。

例

グループにしましょう $G = \lbrace 1, i, -1, -i \rbrace$

次に、いくつかのサブグループは $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$、

これはサブグループではありません- $H_3 = \lbrace 1, i \rbrace$ それは $(i)^{-1} = -i$ にありません $H_3$

半順序集合（POSET）

半順序集合は、反射的、反対称的、推移的である二項関係を持つ集合で構成されます。「半順序集合」はPOSETと略されます。

例

• 二項演算での実数のセット以下 $(\le)$ 半順序集合です。

  セットしましょう $S = \lbrace 1, 2, 3 \rbrace$ そして操作は $\le$

  関係は $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$

  この関係Rは次のように反射的です $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$

  この関係Rは、次のように反対称です。

  $\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$

  この関係Rは、次のように推移的でもあります。 $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$。

  したがって、それは poset。

• 演算「到達可能性」の下での有向非巡回グラフの頂点セットは半順序集合です。

ハッセ図

ポセットのハッセ図は、頂点がそのポセットの要素であり、円弧がポセットのペア（x​​、y）をカバーする有向グラフです。ポセットの場合$x < y$の場合、点xはハッセ図の点yよりも低く表示されます。場合$x<y<z$ ポセットでは、矢印は暗黙的であるため、xとzの間に表示されません。

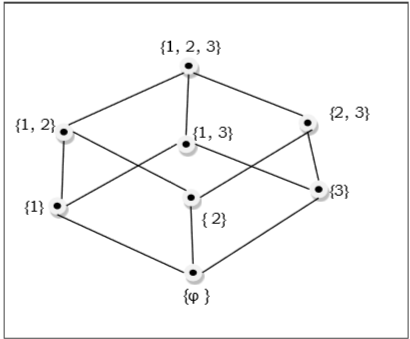
例

のサブセットの半順序集合 $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ 次のハッセ図で示されています-

線形順序のセット

線形順序セットまたは全順序セットは、要素のすべてのペアが比較可能な半順序セットです。要素$a, b \in S$ どちらかが同等であると言われています $a \le b$ または $b \le a$保持します。三分法は、この順序集合の合計を定義します。全順序集合は、次の特性を持つ分配束として定義できます。$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ セットSのaとbのすべての値に対して。

例

のべき集合 $\lbrace a, b \rbrace$ \ subseteqによって順序付けられたものは、べき集合のすべての要素として完全に順序付けられたセットです。 $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ 同等です。

非合計注文セットの例

セット $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 動作中、xはyを除算し、順序集合の合計ではありません。

ここで、すべてのために $(x, y) \in S, x | y$保持する必要がありますが、2 | 3、2は3を分割しない、または3は2を分割しないため、これは完全な順序集合ではありません。

格子

格子は半順序集合です $(L, \le)$ すべてのペア $\lbrace a, b \rbrace \in L$ 最小の上限があります（ $a \lor b$）および最大の下限（で示される） $a \land b$）。LUB$(\lbrace a,b \rbrace)$aとbの結合と呼ばれます。GLB$(\lbrace a,b \rbrace )$ aとbの出会いと呼ばれます。

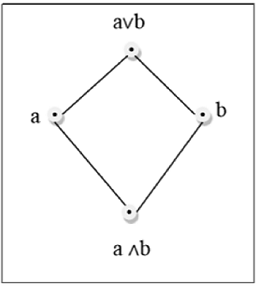
例

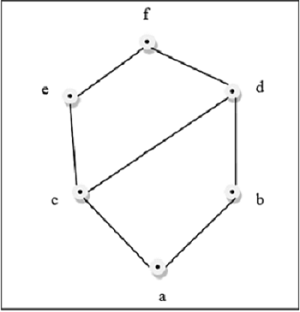
この上の図は、すべてのペアについて $\lbrace a, b \rbrace \in L$、GLBとLUBが存在します。

この上の図は格子ではありません。 $GLB (a, b)$ そして $LUB (e, f)$ 存在しません。

他のいくつかのラティスについて以下で説明します-

有界格子

格子Lは、最大要素1と最小要素0がある場合、有界格子になります。

可補束

格子Lは、それが有界格子であり、格子内のすべての要素に補集合がある場合、可補束になります。要素xは、次の場合に補数x 'を持ちます。$\exists x(x \land x’=0 and x \lor x’ = 1)$

分配束

格子が次の2つの分配特性を満たす場合、それは分配束と呼ばれます。

• $a \lor (b \land c) = (a \lor b) \land (a \lor c)$

• $a \land (b \lor c) = (a \land b) \lor (a \land c)$

モジュラー束

格子が次の特性を満たす場合、それはモジュラー格子と呼ばれます。

$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$

格子の性質

べき等プロパティ

• $a \lor a = a$

• $a \land a = a$

吸収特性

• $a \lor (a \land b) = a$

• $a \land (a \lor b) = a$

可換性

• $a \lor b = b \lor a$

• $a \land b = b \land a$

結合法則

• $a \lor (b \lor c) = (a \lor b) \lor c$

• $a \land (b \land c) = (a \land b) \land c$

格子の双対

格子の双対は、 'を交換することによって得られます$\lor$'と'$\land$' 操作。

例

の双対 $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$

日常生活では、多くの場合、一連のイベントのすべての可能な結果の数を見つける必要があります。たとえば、男性50人と女性38人の中から、男性6人と女性4人で構成される審査員団をどのように選ぶことができるでしょうか。最初の5文字が大文字のアルファベット、次の4文字が数字、最後の文字が再び大文字になるように、10文字のPAN番号をいくつ生成できますか。これらの問題を解決するために、カウントの数学的理論が使用されます。Counting 主に、基本的なカウントルール、順列ルール、および組み合わせルールが含まれます。

合計と積の規則

ザ・ Rule of Sum そして Rule of Product 難しいカウントの問題を単純な問題に分解するために使用されます。

• The Rule of Sum −一連のタスクの場合 $T_1, T_2, \dots, T_m$ で行うことができます $w_1, w_2, \dots w_m$ それぞれの方法（条件は、タスクを同時に実行できないことです）、これらのタスクの1つを実行する方法の数は次のとおりです。 $w_1 + w_2 + \dots +w_m$。互いに素な2つのタスクAとBを検討すると（つまり、$A \cap B = \emptyset$）、次に数学的に $|A \cup B| = |A| + |B|$

• The Rule of Product −一連のタスクの場合 $T_1, T_2, \dots, T_m$ で行うことができます $w_1, w_2, \dots w_m$ それぞれの方法とすべてのタスクが前のタスクの発生後に到着すると、 $w_1 \times w_2 \times \dots \times w_m$タスクを実行する方法。数学的には、タスクBがタスクAの後に到着した場合、$|A \times B| = |A|\times|B|$

例

Question−少年はXに住んでいて、Zの学校に行きたいと思っています。自宅のXから、最初にYに到達し、次にYからZに到達する必要があります。3つのバスルートまたは2つの電車ルートのいずれかでXからYに移動できます。そこから、彼はZに到達するために4つのバスルートまたは5つの電車ルートを選択できます。XからZに行くにはいくつの方法がありますか？

Solution − XからYまで、彼は入ることができます $3 + 2 = 5$方法（数え上げの和則）。その後、彼はYからZに行くことができます$4 + 5 = 9$方法（数え上げの和則）。したがって、XからZまで彼は入ることができます$5 \times 9 = 45$ 方法（製品のルール）。

順列

A permutation順序が重要ないくつかの要素の配置です。言い換えれば、順列は要素の順序付けられた組み合わせです。

例

• 一度に2つを取ることによる集合S = {x、y、z}から、すべての順列は−です。

  $ xy, yx, xz, zx, yz, zy $。

• 一連の数字から3桁の数字の順列を形成する必要があります $S = \lbrace 1, 2, 3 \rbrace$。数字を並べると、異なる3桁の数字が形成されます。順列は= 123、132、213、231、312、321になります

順列の数

一度に「r」が取られる「n」個の異なるものの順列の数は、で表されます。 $n_{P_{r}}$

$$n_{P_{r}} = \frac{n!}{(n - r)!}$$

どこ $n! = 1.2.3. \dots (n - 1).n$

Proof −「n」個の異なる要素があるとします。

そもそも埋める方法はn通りあります。最初の場所（n-1）を埋めた後、要素の数が残ります。したがって、2位を埋める方法は（n-1）あります。1位と2位を埋めた後、（n-2）個の要素が残ります。したがって、3位を埋めるには（n-2）の方法があります。これで、r番目の場所を埋める方法の数を[n –（r–1）] = n–r +1として一般化できます。

だから、合計はありません。1位からr位まで埋める方法の例−

$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$

$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$

したがって、

$n_{ P_{ r } } = n! / (n-r)!$

順列のいくつかの重要な式

• ある場合はn個の要素は、$a_1$ ある種の似ている、 $a_2$ 別の種類に似ています。 $a_3$ 第三種などに似ています $a_r$ の $r^{th}$ 種類、どこ $(a_1 + a_2 + ... a_r) = n$。

  次に、これらのn個のオブジェクトの順列の数は=です。 $n! / [(a_1!(a_2!) \dots (a_r!)]$。

• 一度にn個の要素を取るn個の異なる要素の順列の数= $n_{P_n} = n!$

• x個の特定のものが常に特定の場所を占める場合に一度にr個の要素をとるn個の異なる要素の順列の数= $n-x_{p_{r-x}}$

• r個の指定されたものが常に一緒になるときのn個の異なる要素の順列の数は-です。 $r! (n−r+1)!$

• r個の指定されたものが決して一緒にならないときのn個の異なる要素の順列の数は-です。 $n!–[r! (n−r+1)!]$

• 時間にx要素を取得したn個の異なる要素の循環順列の数= $^np_{x}/x$

• n個の異なるものの循環順列の数= $^np_{n}/n$

いくつかの問題

Problem 1 − 6種類のカードの束から、それを並べ替える方法はいくつありますか？

Solution − 6枚のカードのデッキから一度に6枚のカードを取っているので、順列は次のようになります。 $^6P_{6} = 6! = 720$

Problem 2 −「READER」という単語の文字はどのように配置できますか？

Solution −「READER」という単語には6文字の単語（2 E、1 A、1D、2R）があります。

順列は次のようになります $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$

Problem 3 −子音が偶数の位置のみを占めるように、「ORANGE」という単語の文字をどのように配置できますか。

Solution−「ORANGE」という単語には3つの母音と3つの子音があります。子音をそれらの間で配置する方法の数$= ^3P_{3} = 3! = 6$。残りの3つの空いている場所は3つの母音で埋められます$^3P_{3} = 3! = 6$方法。したがって、順列の総数は次のようになります。$6 \times 6 = 36$

組み合わせ

A combination 順序が重要ではないいくつかの特定の要素の選択です。

一度にr個取られるn個のすべての組み合わせの数は-です。

$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$

Problem 1

セットのサブセットの数を見つける $\lbrace1, 2, 3, 4, 5, 6\rbrace$ 3つの要素を持っています。

Solution

セットのカーディナリティは6であり、セットから3つの要素を選択する必要があります。ここでは、順序は重要ではありません。したがって、サブセットの数は次のようになります。$^6C_{3} = 20$。

Problem 2

部屋には男性6人と女性5人がいます。部屋から男性3人と女性2人を選ぶ方法はいくつありますか？

Solution

6人の男性から3人の男性を選ぶ方法の数は $^6C_{3}$ 5人の女性から2人の女性を選ぶ方法の数は $^5C_{2}$

したがって、ウェイの総数は-です。 $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$

Problem 3

合計9人の学生から3人の学生の3つの異なるグループを選択する方法はいくつありますか？

Solution

グループに1、2、3の番号を付けましょう

^最初のグループに3人の学生を選ぶために、方法の数-$^9C_{3}$

2のための3人の学生の選択のためのいくつかの方法^ND第一グループを選択した後、グループを-$^6C_{3}$

3のための3人の学生の選択のためのいくつかの方法^番目の1選択した後、グループを^目と2^回目のグループを-$^3C_{3}$

したがって、ウェイの総数 $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$

パスカルのアイデンティティ

第17パスカルによって導出パスカルのアイデンティティ、^目世紀、n個の要素からk個の要素を選択する方法の数は、（n-1）個の要素から（K-1）の要素を選択する方法の数の和に等しくなる状態n-1個の要素から要素を選択する方法の数。

数学的には、任意の正の整数kおよびnの場合： $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$

Proof −

$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$

$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$

$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$

$= (n-1)! \frac{ n } { k!(n-k)! }$

$= \frac{ n! } { k!(n-k)! }$

$= n_{ C_{ k } }$

鳩の巣原理

1834年、ドイツの数学者、ペーターグスタフレジューヌディリクレは、彼が引き出しの巣原理と呼んだ原理を述べま​​した。現在、それは鳩の巣原理として知られています。

Pigeonhole Principle鳩の総数よりも鳩の穴が少なく、各鳩が鳩の穴に入れられる場合、複数の鳩がいる鳩の穴が少なくとも1つある必要があると述べています。n> mのm個の鳩の穴にn個の鳩を入れると、複数の鳩がいる穴ができます。

例

• 10人の男性が部屋にいて、握手に参加しています。各人が少なくとも1回握手し、同じ男性の手を2回以上握る人がいない場合、2人の男性が同じ回数の握手に参加しました。

• 30人のクラスには、名前が同じアルファベットで始まる人が少なくとも2人いる必要があります。

包除原理

ザ・ Inclusion-exclusion principle複数の互いに素でない集合の和集合の基数を計算します。2つのセットAとBの場合、原則は次のように述べます。

$|A \cup B| = |A| + |B| - |A \cap B|$

3つのセットA、B、およびCの場合、原則は次のように述べます。

$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$

一般化された式-

$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$

Problem 1

1から50までの整数は2または3の倍数ですが、両方ではありませんか？

Solution

1から100まで、 $50/2 = 25$ 2の倍数である数。

がある $50/3 = 16$ 3の倍数である数。

がある $50/6 = 8$ 2と3の両方の倍数である数。

そう、 $|A|=25$、 $|B|=16$ そして $|A \cap B|= 8$。

$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$

Problem 2

50人の学生のグループでは、24人が冷たい飲み物が好きで36人が熱い飲み物が好きで、各学生は2つの飲み物のうち少なくとも1つが好きです。コーヒーとお茶の両方が好きな人は何人いますか？

Solution

Xを冷たい飲み物が好きな学生のセット、Yを熱い飲み物が好きな人々のセットとします。

そう、 $| X \cup Y | = 50$、 $|X| = 24$、 $|Y| = 36$

$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$

したがって、お茶とコーヒーの両方が好きな学生は10人います。

カウントの概念に密接に関連しているのは確率です。カードゲーム、スロットマシン、宝くじなど、運が左右するゲームの結果を推測しようとすることがよくあります。つまり、特定の結果が得られる可能性または確率を見つけようとします。

Probabilityイベントの発生の可能性を見つけることとして概念化することができます。数学的には、それはランダムプロセスとその結果の研究です。確率の法則は、遺伝学、天気予報、世論調査、株式市場などのさまざまな分野に広く適用できます。

基本概念

確率論は、偶然に関する数学の問題を扱っていた2人のフランスの数学者、ブレーズパスカルとピエールドフェルマーによって17世紀に発明されました。

確率の詳細に進む前に、いくつかの定義の概念を理解しましょう。

Random Experiment−考えられるすべての結果がわかっていて、正確な出力を事前に予測できない実験は、ランダム実験と呼ばれます。公正なコインを投げることは、ランダムな実験の一例です。

Sample Space−実験を実行するとき、考えられるすべての結果の集合Sはサンプル空間と呼ばれます。コインを投げるとサンプルスペース$S = \left \{ H, T \right \}$

Event−サンプル空間のサブセットはイベントと呼ばれます。コインを投げた後、頭を上にするのはイベントです。

「確率」という言葉は、特定のイベントが発生する可能性を意味します。私たちが言える最善のことは、確率の概念を使用して、それらが発生する可能性がどれほどあるかです。

$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$

イベントの発生は0％から100％の間で変化するため、確率は0から1の間で変化します。

確率を見つけるための手順

ステップ1-実験のすべての可能な結果を​​計算します。

ステップ2-実験の好ましい結果の数を計算します。

ステップ3-対応する確率式を適用します。

コインを投げる

コインが投げられた場合、2つの可能な結果があります-頭 $(H)$ またはテール $(T)$

したがって、結果の総数= 2

したがって、頭を取得する確率 $(H)$ 上は1/2で、テールを取得する確率は $(T)$ 上は1/2です

サイコロを投げる

サイコロが投げられたとき、6つの可能な結果が一番上にある可能性があります- $1, 2, 3, 4, 5, 6$。

いずれかの数字の確率は1/6です

偶数になる確率は3/6 = 1/2

奇数になる確率は3/6 = 1/2

デッキからカードを取る

52枚のカードのデッキから、1枚のカードが選ばれた場合、エースが引かれる確率と、ダイアモンドが引かれる確率を見つけます。

考えられる結果の総数-52

エースであることの結果− 4

エースになる確率= 4/52 = 1/13

ダイヤモンドである確率= 13/52 = 1/4

確率の公理

• イベントの確率は常に0から1まで変化します。 $[0 \leq P(x) \leq 1]$

• 不可能なイベントの場合、確率は0であり、特定のイベントの場合、確率は1です。

• あるイベントの発生が別のイベントの影響を受けない場合、それらは相互に排他的または互いに素であると呼ばれます。

  場合 $A_1, A_2....A_n$ 相互に排他的/ばらばらのイベントである場合 $P(A_i \cap A_j) = \emptyset $ にとって $i \ne j$ そして $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$

確率の特性

• 2つのイベントがある場合 $x$ そして $\overline{x}$これらが相補的である場合、相補的イベントの確率は-です。

  $$p(\overline{x}) = 1-p(x)$$

• 2つの非ばらばらのイベントAとBの場合、2つのイベントの和集合の確率-

  $P(A \cup B) = P(A) + P(B)$

• イベントAが別のイベントBのサブセットである場合（つまり、 $A \subset B$）の場合、Aの確率はBの確率以下です。したがって、 $A \subset B$ 意味する $P(A) \leq p(B)$

条件付き確率

イベントBの条件付き確率は、イベントAがすでに発生している場合にイベントが発生する確率です。これは次のように書かれています$P(B|A)$。

数学的に- $ P(B|A) = P(A \cap B)/ P(A)$

イベントAとBが相互に排他的である場合、イベントAの後のイベントBの条件付き確率は、イベントBの確率になります。 $P(B)$。

Problem 1

国では、すべての10代の若者の50％が自転車を所有し、すべての10代の若者の30％が自転車と自転車を所有しています。10代の若者が自転車を所有しているとすると、10代の若者が自転車を所有する確率はどれくらいですか？

Solution

Aは10代の若者が自転車だけを所有しているイベントであり、Bは10代の若者が自転車だけを所有しているイベントであると仮定します。

そう、 $P(A) = 50/100 = 0.5$ そして $P(A \cap B) = 30/100 = 0.3$ 与えられた問題から。

$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$

したがって、ティーンエイジャーが自転車を所有している場合、ティーンエイジャーが自転車を所有している確率は60％です。

Problem 2

クラスでは、全生徒の50％がクリケットをプレイし、全生徒の25％がクリケットとバレーボールをプレイします。学生がクリケットをする場合、学生がバレーボールをする確率はどれくらいですか？

Solution

Aはクリケットのみをプレイする学生のイベントであり、Bはバレーボールのみをプレイする学生のイベントであると仮定します。

そう、 $P(A) = 50/100 =0.5$ そして $P(A \cap B) = 25/ 100 =0.25$ 与えられた問題から。

$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$

したがって、学生がクリケットをする場合、学生がバレーボールをする確率は50％です。

Problem 3

6台の良いラップトップと3台の欠陥のあるラップトップが混同されています。欠陥のあるラップトップを見つけるために、それらすべてがランダムに1つずつテストされます。最初の2つのピックで欠陥のあるラップトップの両方を見つける確率はどれくらいですか？

Solution

Aを最初のテストで欠陥のあるラップトップを見つけたイベントとし、Bを2番目のテストで欠陥のあるラップトップを見つけたイベントとします。

したがって、 $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$

ベイズの定理

Theorem − AとBが2つの相互に排他的なイベントである場合、ここで $P(A)$ Aの確率であり、 $P(B)$ Bの確率です。 $P(A | B)$ Bが真であると仮定した場合のAの確率です。 $P(B | A)$ は、Aが真であると仮定した場合のBの確率であり、ベイズの定理は次のように述べています。

$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$

ベイズの定理の適用

• サンプル空間のすべてのイベントが相互に排他的なイベントである状況。

• どちらかの状況で $P( A_i \cap B )$ それぞれについて $A_i$ または $P( A_i )$ そして $P(B|A_i)$ それぞれについて $A_i$ 知られている。

Problem

3つのペンスタンドを考えてみましょう。最初のペンスタンドには、2本の赤いペンと3本の青いペンが含まれています。2番目のペンには3本の赤いペンと2本の青いペンがあります。3番目のペンには4本の赤いペンと1本の青いペンがあります。各ペンスタンドが選択される確率は同じです。1本のペンがランダムに描かれた場合、それが赤いペンである確率はどのくらいですか？

Solution

しましょう $A_i$i^番目のペンスタンドが選択されたイベントになります。

ここで、i = 1,2,3です。

ペンスタンドを選ぶ確率は等しいので、 $P(A_i) = 1/3$

赤ペンが描かれたイベントをBとします。

最初のペンスタンドの5本のペンの中から赤いペンが選ばれる確率。

$P(B|A_1) = 2/5$

2番目のペンスタンドの5本のペンの中から赤いペンが選択される確率。

$P(B|A_2) = 3/5$

3番目のペンスタンドの5本のペンの中から赤いペンが選択される確率。

$P(B|A_3) = 4/5$

ベイズの定理によると、

$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$

$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$

$= 3/5$

Mathematical inductionは、結果を証明したり、自然数のステートメントを確立したりするための手法です。このパートでは、さまざまな例を通じてこの方法を説明します。

定義

Mathematical Induction は、ステートメント、式、または定理がすべての自然数に当てはまることを証明するために使用される数学的手法です。

この手法には、以下に示すように、ステートメントを証明するための2つのステップが含まれます。

Step 1(Base step) −初期値に対してステートメントが真であることを証明します。

Step 2(Inductive step)−ステートメントがn^番目の反復（または数n）に当てはまる場合、（n + 1）^番目の反復（または数n + 1）にも当てはまることを証明します。

どうやるか

Step 1−ステートメントが真である初期値を検討します。n =初期値の場合にステートメントが真であることを示します。

Step 2− n = kの任意の値に対してステートメントが真であると想定します。次に、ステートメントがn = k +1に対して真であることを証明します。実際には、n = k + 1を2つの部分に分割し、一方の部分はn = k（すでに証明済み）であり、もう一方の部分を証明しようとします。

問題1

$3^n-1$ n = 1、2、..の場合、は2の倍数です。

Solution

Step 1 −の場合 $n = 1, 3^1-1 = 3-1 = 2$ これは2の倍数です

Step 2 −仮定しましょう $3^n-1$ に当てはまります $n=k$、したがって、 $3^k -1$ 本当です（それは仮定です）

私たちはそれを証明しなければなりません $3^{k+1}-1$ 2の倍数でもあります

$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$

最初の部分 $(2 \times 3k)$ 2の倍数であることが確実であり、2番目の部分 $(3k -1)$ 以前の仮定としても当てはまります。

したがって、 $3^{k+1} – 1$ 2の倍数です。

だから、それは証明されています $3^n – 1$ 2の倍数です。

問題2

$1 + 3 + 5 + ... + (2n-1) = n^2$ にとって $n = 1, 2, \dots $

Solution

Step 1 −の場合 $n=1, 1 = 1^2$したがって、ステップ1は満たされます。

Step 2 −ステートメントが真であると仮定しましょう $n=k$。

したがって、 $1 + 3 + 5 + \dots + (2k-1) = k^2$ 本当です（それは仮定です）

私たちはそれを証明しなければなりません $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ も保持します

$1 + 3 + 5 + \dots + (2(k+1) - 1)$

$= 1 + 3 + 5 + \dots + (2k+2 - 1)$

$= 1 + 3 + 5 + \dots + (2k + 1)$

$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$

$= k^2 + (2k + 1)$

$= (k + 1)^2$

そう、 $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ ステップ2を満たすホールド。

したがって、 $1 + 3 + 5 + \dots + (2n - 1) = n^2$ 証明されています。

問題3

証明してください $(ab)^n = a^nb^n$ すべての自然数に当てはまります $n$

Solution

Step 1 −の場合 $n=1, (ab)^1 = a^1b^1 = ab$したがって、ステップ1は満たされます。

Step 2 −ステートメントが真であると仮定しましょう $n=k$、したがって、 $(ab)^k = a^kb^k$ 真です（これは仮定です）。

私たちはそれを証明しなければなりません $(ab)^{k+1} = a^{k+1}b^{k+1}$ も保持

与えられた、 $(ab)^k = a^k b^k$

または、 $(ab)^k (ab) = (a^k b^k ) (ab)$ [両側に「ab」を掛ける]

または、 $(ab)^{k+1} = (aa^k) ( bb^k)$

または、 $(ab)^{k+1} = (a^{k+1}b^{k+1})$

したがって、ステップ2が証明されます。

そう、 $(ab)^n = a^nb^n$ すべての自然数nに当てはまります。

強い帰納法

強い帰納法は、数学的帰納法のもう1つの形式です。この誘導手法を通じて、命題関数が$P(n)$ すべての正の整数に当てはまります。 $n$、次の手順を使用して-

• Step 1(Base step) −それは最初の命題が $P(1)$ 本当。

• Step 2(Inductive step) −条件文が $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ 正の整数の場合はtrue $k$。

この章では、再帰的手法を使用してシーケンスを導出し、カウントの問題を解決する方法について説明します。シーケンスの項を再帰的に見つける手順は、recurrence relation。線形漸化式の理論とその解を研究します。最後に、漸化式を解くための母関数を紹介します。

定義

漸化式は、次の項が前の項の関数であるシーケンスを再帰的に定義する方程式です（式 $F_n$ のいくつかの組み合わせとして $F_i$ と $i < n$）。

Example −フィボナッチ数列− $F_n = F_{n-1} + F_{n-2}$、ハノイの塔− $F_n = 2F_{n-1} + 1$

線形漸化式

次数kまたは次数kの線形漸化式は、次の形式の漸化式です。 $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $（（$A_n$ は定数であり、 $A_k \neq 0$）1次多項式としての数列。

これらは線形漸化式のいくつかの例です-

漸化式	初期値	ソリューション
F n = F n-1 + F n-2	a 1 = a 2 = 1	フィボナッチ数
F n = F n-1 + F n-2	a 1 = 1、a 2 = 3	リュカ数
F n = F n-2 + F n-3	a 1 = a 2 = a 3 = 1	パドヴァン数列
F n = 2F n-1 + F n-2	a 1 = 0、a 2 = 1	ペル数

線形漸化式を解く方法

2次の線形漸化式が-であると仮定します。 $F_n = AF_{n-1} +BF_{n-2}$ ここで、AとBは実数です。

上記の漸化式の特性式は次のとおりです。

$$x^2 - Ax - B = 0$$

根を見つける間に3つのケースが発生する可能性があります-

Case 1 −この方程式が次のように因数分解する場合 $(x- x_1)(x- x_1) = 0$ そしてそれは2つの異なる実根を生成します $x_1$ そして $x_2$、その後 $F_n = ax_1^n+ bx_2^n$解決策です。[ここで、aとbは定数です]

Case 2 −この方程式が次のように因数分解する場合 $(x- x_1)^2 = 0$ そしてそれは単一の実根を生成します $x_1$、その後 $F_n = a x_1^n+ bn x_1^n$ 解決策です。

Case 3 −方程式が2つの異なる複素根を生成する場合、 $x_1$ そして $x_2$ 極形式で $x_1 = r \angle \theta$ そして $x_2 = r \angle(- \theta)$、その後 $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ 解決策です。

Problem 1

漸化式を解く $F_n = 5F_{n-1} - 6F_{n-2}$ どこ $F_0 = 1$ そして $F_1 = 4$

Solution

漸化式の特性方程式は次のとおりです。

$$x^2 - 5x + 6 = 0,$$

そう、 $(x - 3) (x - 2) = 0$

したがって、根は-

$x_1 = 3$ そして $x_2 = 2$

ルーツは本物ではっきりしています。つまり、これはケース1の形式です。

したがって、解は次のようになります。

$$F_n = ax_1^n + bx_2^n$$

ここに、 $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$

したがって、

$1 = F_0 = a3^0 + b2^0 = a+b$

$4 = F_1 = a3^1 + b2^1 = 3a+2b$

これらの2つの方程式を解くと、次のようになります。 $ a = 2$ そして $b = -1$

したがって、最終的な解決策は次のとおりです。

$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$

Problem 2

漸化式を解く- $F_n = 10F_{n-1} - 25F_{n-2}$ どこ $F_0 = 3$ そして $F_1 = 17$

Solution

漸化式の特性方程式は次のとおりです。

$$ x^2 - 10x -25 = 0$$

そう $(x - 5)^2 = 0$

したがって、単一の実根があります $x_1 = 5$

単一の実数値ルートがあるため、これはケース2の形式になります。

したがって、解は次のようになります。

$F_n = ax_1^n + bnx_1^n$

$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$

$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$

これらの2つの方程式を解くと、次のようになります。 $a = 3$ そして $b = 2/5$

したがって、最終的な解決策は次のとおりです。 $F_n = 3.5^n +( 2/5) .n.2^n $

Problem 3

漸化式を解く $F_n = 2F_{n-1} - 2F_{n-2}$ どこ $F_0 = 1$ そして $F_1 = 3$

Solution

漸化式の特性方程式は次のとおりです。

$$x^2 -2x -2 = 0$$

したがって、根は-

$x_1 = 1 + i$ そして $x_2 = 1 - i$

極形式では、

$x_1 = r \angle \theta$ そして $x_2 = r \angle(- \theta),$ どこ $r = \sqrt 2$ そして $\theta = \frac{\pi}{4}$

ルーツは架空のものです。したがって、これはケース3の形式です。

したがって、解は次のようになります。

$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$

$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$

$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$

これらの2つの方程式を解くと $a = 1$ そして $b = 2$

したがって、最終的な解決策は次のとおりです。

$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$

不均一な漸化式と特定の解決策

漸化式は、次の形式の場合、不均一と呼ばれます。

$F_n = AF_{n-1} + BF_{n-2} + f(n)$ どこ $f(n) \ne 0$

その関連する同次漸化式は $F_n = AF_{n–1} + BF_{n-2}$

ソリューション $(a_n)$ 不均一な漸化式には2つの部分があります。

最初の部分は解決策です $(a_h)$ 関連する同次漸化式の2番目の部分は特定の解です $(a_t)$。

$$a_n=a_h+a_t$$

最初の部分の解決策は、前のセクションで説明した手順を使用して行われます。

特定の解決策を見つけるために、適切な試行解決策を見つけます。

しましょう $f(n) = cx^n$; しましょう$x^2 = Ax + B$ 関連する同次漸化式の特性方程式であり、 $x_1$ そして $x_2$ そのルーツになります。

• 場合 $x \ne x_1$ そして $x \ne x_2$、その後 $a_t = Ax^n$

• 場合 $x = x_1$、 $x \ne x_2$、その後 $a_t = Anx^n$

• 場合 $x = x_1 = x_2$、その後 $a_t = An^2x^n$

例

不均一な漸化式を $F_n = AF_{n–1} + BF_{n-2} + f(n)$ 特徴的なルーツを持つ $x_1 = 2$ そして $x_2 = 5$。のさまざまな可能な値の試行ソリューション$f(n)$ 次のとおりです-