離散数学-関係

セットが議論されているときはいつでも、セットの要素間の関係が次に浮かび上がります。 Relations 同じセットのオブジェクト間、または2つ以上のセットのオブジェクト間に存在する場合があります。

定義とプロパティ

セットxからyへの二項関係R（$ xRy $または$ R（x、y）$として記述）は、デカルト積$ x \ times y $のサブセットです。Gの順序対が逆になると、関係も変化します。

一般に、集合$ A_1、\ dots、\、および\ A_n $間のn項関係Rは、n項積$ A_1 \ times \ dots \ times A_n $のサブセットです。この場合、関係Rの最小カーディナリティはゼロであり、最大は$ n ^ 2 $です。

単一の集合Aの二項関係Rは、$ A \ times A $のサブセットです。

それぞれカーディナリティmとnを持つ2つの異なるセットAとBの場合、AからBへの関係Rの最大カーディナリティはmnです。

ドメインと範囲

2つのセットAとBがあり、関係Rの順序対（x、y）がある場合、-

ザ・ domainRのDom（R）は、集合$ \ lbrace x \：|です。\ ：（ x、y）\ in R \：for \：some \：y \：in \：B \ rbrace $
ザ・ range RのRan（R）は、集合$ \ lbrace y \：| \ ：（ x、y）\ in R \：for \：some \：x \：in \：A \ rbrace $

例

$ A = \ lbrace 1、2、9 \ rbrace $および$ B = \ lbrace 1、3、7 \ rbrace $

ケース1-関係Rが「等しい」の場合、$ R = \ lbrace（1、1）、（3、3）\ rbrace $

Dom（R）= $ \ lbrace 1、3 \ rbrace、Ran（R）= \ lbrace 1、3 \ rbrace $
ケース2-関係Rが「より小さい」の場合、$ R = \ lbrace（1、3）、（1、7）、（2、3）、（2、7）\ rbrace $

Dom（R）= $ \ lbrace 1、2 \ rbrace、Ran（R）= \ lbrace 3、7 \ rbrace $
ケース3-関係Rが「より大きい」の場合、$ R = \ lbrace（2、1）、（9、1）、（9、3）、（9、7）\ rbrace $

Dom（R）= $ \ lbrace 2、9 \ rbrace、Ran（R）= \ lbrace 1、3、7 \ rbrace $

グラフを使用した関係の表現

関係は、有向グラフを使用して表すことができます。

グラフ内の頂点の数は、リレーションが定義されているセット内の要素の数と同じです。関係Rの順序対（x、y）ごとに、頂点 'x'から頂点 'y'への有向エッジがあります。順序対（x、x）がある場合、頂点 'x'に自己ループがあります。

セット$ S = \ lbrace 1、2、3 \ rbrace $に$ R = \ lbrace（1、1）、（1,2）、（3、2）\ rbrace $の関係があるとします。次のグラフで表されます-

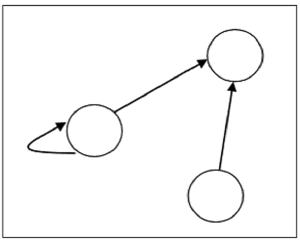
関係の種類

ザ・ Empty Relation セットXとYの間、またはEには、空のセット$ \ emptyset $があります。
ザ・ Full Relation セットXとYの間はセット$ X \ times Y $
ザ・ Identity RelationセットXには、セット$ \ lbrace（x、x）|があります。x \ in X \ rbrace $
関係Rの逆関係R 'は、次のように定義されます。− $ R' = \ lbrace（b、a）| （a、b）\ in R \ rbrace $

Example − $ R = \ lbrace（1、2）、（2、3）\ rbrace $の場合、$ R '$は$ \ lbrace（2、1）、（3、2）\ rbrace $になります
セットAの関係Rはと呼ばれます Reflexive $ \ forall a \ in A $が（aRaが保持する）に関連している場合

Example −集合$ X = \ lbrace a、b \ rbrace $の関係$ R = \ lbrace（a、a）、（b、b）\ rbrace $は反射的です。
セットAの関係Rはと呼ばれます Irreflexive $ a \ in A $がaに関連していない場合（aRaは保持されません）。

Example −集合$ X = \ lbrace a、b \ rbrace $の関係$ R = \ lbrace（a、b）、（b、a）\ rbrace $は反射的ではありません。
セットAの関係Rはと呼ばれます Symmetric $ xRy $が$ yRx $を意味する場合、$ \ forall x \ in A $および$ \ forall y \ in A $。

Example −セット$ A = \ lbrace 1、2、3 \ rbrace $の関係$ R = \ lbrace（1、2）、（2、1）、（3、2）、（2、3）\ rbrace $ is対称。
セットAの関係Rはと呼ばれます Anti-Symmetric $ xRy $および$ yRx $が$ x = y \を意味する場合：\ forall x \ in A $および$ \ forall y \ in A $。

Example − $ R = \ lbrace（x、y）\ to N | \：x \ leq y \ rbrace $は、$ x \ leq y $と$ y \ leq x $が$ x = y $を意味するため、反対称です。。
セットAの関係Rはと呼ばれます Transitive $ xRy $および$ yRz $が$ xRzを意味する場合、\ forall x、y、z \ in A $。

Example −集合$ A = \ lbrace 1、2、3 \ rbrace $の関係$ R = \ lbrace（1、2）、（2、3）、（1、3）\ rbrace $は推移的です。
関係は Equivalence Relation それが反射的、対称的、推移的である場合。

Example −関係$ R = \ lbrace（1、1）、（2、2）、（3、3）、（1、2）、（2,1）、（2,3）、（3,2）、（1,3）、（3,1）集合$ A = \ lbrace 1、2、3の\ rbrace $ \ rbrace $は、反射的、対称的、推移的であるため、同値関係です。