원의 분수 부분
완전한 또는 전체 원은 1로 간주되고 원의 일부는 분수로 표시됩니다. 예를 들어, 원이 8 개의 동일한 부분으로 나뉘면 각 부분은 분수 1/8을 나타냅니다. 그러한 원의 세 부분은 3/8 이상을 나타냅니다.
여기서 우리는 원의 특정 부분을 나타내는 분수가 주어지고 원의 나머지 미지 부분을 나타내는 분수를 찾아야하는 문제 유형을 다루고 있습니다. 이러한 문제를 해결하기 위해 분수 부분을 나타내는 분수를 더한 다음 전체 원인 1에서 합계를 뺍니다. 결과는 원의 알려지지 않은 분수 부분을 나타내는 분수를 제공합니다.
얼마나 많은 원이 음영 처리되지 않습니까? 답을 가장 간단한 형태의 분수로 작성하십시오.
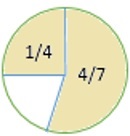
해결책
Step 1:
먼저 그림의 전체 부분이 음영 처리 된 것을 찾습니다.
$ \ frac {1} {4} $ + $ \ frac {4} {7} $ = $ \ frac {7} {28} $ + $ \ frac {16} {28} $ = $ \ frac {(7 +16)} {28} $ = $ \ frac {23} {28} $
Step 2:
음영 처리되지 않은 그림의 비율을 찾기 위해 1에서 얻은 결과 ( $ \ frac {23} {28} $ )를 뺍니다 .
1 − $ \ frac {23} {28} $ = $ \ frac {28} {28} $ − $ \ frac {23} {28} $ = $ \ frac {(28−23} {28} $ = $ \ frac {5} {28} $
따라서 음영 처리되지 않은 그림의 비율은 $ \ frac {5} {28} $ 입니다.
얼마나 많은 원이 음영 처리됩니까? 답을 가장 간단한 형태의 분수로 작성하십시오.
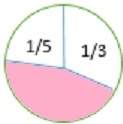
해결책
Step 1:
먼저 우리는 그림이 얼마나 음영이 없는지 알아냅니다.
$ \ frac {1} {5} $ + $ \ frac {1} {3} $ = $ \ frac {3} {15} $ + $ \ frac {5} {15} $ = $ \ frac {(3 +5)} {15} $ = $ \ frac {8} {15} $
Step 2:
음영 처리되지 않은 그림의 비율을 찾기 위해 1에서 얻은 결과 ( $ \ frac {8} {15} $ )를 뺍니다 .
1 − $ \ frac {8} {15} $ = $ \ frac {15} {15} $ − $ \ frac {8} {15} $ = $ \ frac {(15−8)} {15} $ = $ \ frac {7} {15} $
따라서 음영 처리 된 그림의 비율은 $ \ frac {7} {15} $ 입니다.