이산 수학-그룹 이론
세미 그룹
이진 연산 $ '\ omicron'$ (구성)을 사용하는 유한 또는 무한 집합 $ 'S'$는 다음 두 조건을 동시에 유지하는 경우 세미 그룹이라고합니다.
Closure − 모든 쌍 $ (a, b) \ in S, \ :( a \ omicron b) $는 $ S $ 세트에 있어야합니다.
Associative − 모든 원소 $ a, b, c \ in S, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $가 있어야합니다.
예
더하기 연산이있는 양의 정수 세트 (0 제외)는 세미 그룹입니다. 예 : $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $
여기서 클로저 속성은 모든 쌍 $ (a, b) \ in S, (a + b) $가 세트 S에 존재합니다. 예를 들어, $ 1 + 2 = 3 \ in S] $
연관 속성은 모든 요소 $ a, b, c \ in S, (a + b) + c = a + (b + c) $에도 적용됩니다. 예 : $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $
모노 이드
모노 이드는 동일 요소가있는 반 그룹입니다. 집합 S의 식별 요소 ($ e $ 또는 E로 표시)는 모든 요소 $ a \ in S $에 대해 $ (a \ omicron e) = a $와 같은 요소입니다. 식별 요소는unit element. 따라서 모노 이드는 세 가지 속성을 동시에 보유합니다.Closure, Associative, Identity element.
예
곱하기 연산이있는 양의 정수 세트 (0 제외)는 모노 이드입니다. $ S = \ l 중괄호 1, 2, 3, \ dots \ rbrace $
여기서 클로저 속성은 모든 쌍 $ (a, b) \ in S, (a \ times b) $는 세트 S에 존재합니다. [예를 들어, $ 1 \ times 2 = 2 \ in S $ 등]
연관 속성은 모든 요소 $ a, b, c \ in S, (a \ times b) \ times c = a \ times (b \ times c) $ [예 : $ (1 \ times 2) \ times 3 = 1 \ times (2 \ times 3) = 6 $ 등]
Identity 속성은 모든 요소 $ a \ in S, (a \ times e) = a $ [예 : $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ 등]에도 적용됩니다. 여기서 정체성 요소는 1입니다.
그룹
그룹은 역 요소가있는 모노 이드입니다. 집합 S의 역 요소 (I로 표시)는 $ (a \ omicron I) = (I \ omicron a) = a $, 각 요소 $ a \ in S $에 대한 요소입니다. 따라서 그룹은 i) 클로저, ii) 연관성, iii) 동일성 요소, iv) 역 요소의 네 가지 속성을 동시에 보유합니다. 그룹 G의 순서는 G의 요소 수이고 그룹의 요소 순서는 an이 해당 그룹 G의 동일 요소가되는 최소 양의 정수 n입니다.
예
$ N \ times N $ 비 특이 행렬의 집합은 행렬 곱셈 연산에서 그룹을 형성합니다.
두 개의 $ N \ times N $ 비 특이 행렬의 곱은 또한 클로저 특성을 보유하는 $ N \ times N $ 비 특이 행렬입니다.
행렬 곱셈 자체는 연관성이 있습니다. 따라서 연관 속성이 유지됩니다.
$ N \ times N $ 비 특이 행렬 집합에는 항등 요소 속성을 포함하는 단위 행렬이 포함됩니다.
모든 행렬이 비 특수 행렬이기 때문에 모두 비 특수 행렬 인 역 원소를 가지고 있습니다. 따라서 역 속성도 유지됩니다.
아벨 리안 그룹
아벨 그룹 G는 요소 쌍 $ (a, b) \ in G $가 항상 교환 법칙을 유지하는 그룹입니다. 따라서 그룹은 동시에 5 개의 속성을 보유합니다. i) 클로저, ii) 연관성, iii) 동일성 요소, iv) 역 요소, v) 교환.
예
더하기 연산이있는 양의 정수 세트 (0 포함)는 아벨 그룹입니다. $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $
여기서 클로저 속성은 모든 쌍 $ (a, b) \ in S, (a + b) $가 세트 S에 존재합니다. [예를 들어, $ 1 + 2 = 2 \ in S $ 등]
연관 속성은 모든 요소 $ a, b, c \ in S, (a + b) + c = a + (b + c) $ [예 : $ (1 +2) + 3 = 1 + (2 + 3) = 6 $ 등]
Identity 속성은 모든 요소 $ a \ in S, (a \ times e) = a $ [예 : $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ 등]에도 적용됩니다. 여기서 identity 요소는 1입니다.
교환 속성은 또한 모든 요소 $ a \ in S, (a \ times b) = (b \ times a) $ [예 : $ (2 \ times 3) = (3 \ times 2) = 3 $ 등 의 위에]
순환 그룹 및 하위 그룹
ㅏ cyclic group단일 요소로 생성 할 수있는 그룹입니다. 순환 그룹의 모든 요소는 생성기라고하는 특정 요소의 힘입니다. 순환 그룹은 생성기 'g'에 의해 생성 될 수 있으므로 그룹의 다른 모든 요소는 생성기 'g'의 거듭 제곱으로 기록 될 수 있습니다.
예
곱셈 연산에서 복소수 세트 $ \ lbrace 1, -1, i, -i \ rbrace $는 순환 그룹입니다.
두 개의 생성기가 있습니다. $ i $ 및 $ –i $ as $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ 및 $ (– i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $는 그룹의 모든 요소를 포함합니다. 따라서 그것은 순환 그룹입니다.
Note − A cyclic group항상 아벨 그룹이지만 모든 아벨 그룹이 순환 그룹 인 것은 아닙니다. 덧셈의 유리수는 순환 적이 지 않지만 아벨입니다.
ㅏ subgroup H는 그룹 G의 하위 집합입니다 ($ H ≤ G $로 표시) 4 개의 속성을 동시에 충족하는 경우 − Closure, Associative, Identity element, 및 Inverse.
전체 그룹 G를 포함하지 않는 그룹 G의 하위 그룹 H를 적절한 하위 그룹이라고합니다 ($ H <G $로 표시). 순환 그룹의 하위 그룹은 순환이고 아벨 하위 그룹도 아벨입니다.
예
그룹 $ G = \ lbrace 1, i, -1, -i \ rbrace $
그러면 일부 하위 그룹은 $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,
이것은 부분 군이 아닙니다 − $ H_3 = \ lbrace 1, i \ rbrace $ 왜냐하면 $ (i) ^ {-1} = -i $가 $ H_3 $에 없기 때문입니다.
부분 주문 세트 (POSET)
부분적으로 정렬 된 집합은 반사적이고 반대 칭이며 전이적인 이진 관계를 가진 집합으로 구성됩니다. "일부 주문 세트"는 POSET로 축약됩니다.
예
$ (\ le) $보다 작거나 같은 이진 연산에서 실수 세트는 포셋입니다.
$ S = \ lbrace 1, 2, 3 \ rbrace $로 설정하고 연산은 $ \ le $입니다.
관계는 $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $입니다.
이 관계 R은 $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $로 반사적입니다.
이 관계 R은 반대 칭입니다.
$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ and \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $
이 관계 R은 $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ in R $로 전이됩니다.
따라서 poset.
'도달 가능성'작업에서 방향성 비순환 그래프의 꼭지점 집합은 포셋입니다.
Hasse 다이어그램
포셋의 Hasse 다이어그램은 정점이 해당 포셋의 요소이고 호가 포셋의 쌍 (x, y)을 덮는 방향성 그래프입니다. 포셋 $ x <y $에있는 경우 점 x는 Hasse 다이어그램의 점 y보다 낮게 나타납니다. 포셋에서 $ x <y <z $이면 암시 적이므로 x와 z 사이에 화살표가 표시되지 않습니다.
예
$ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $는 다음 Hasse 다이어그램에 표시됩니다.
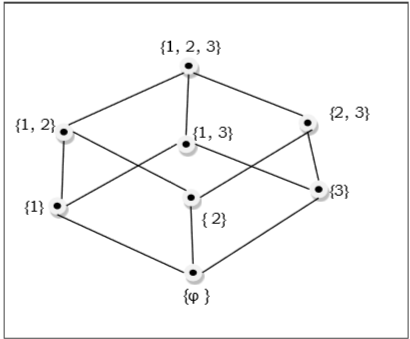
선형 정렬 된 세트
선형 순서 집합 또는 전체 순서 집합은 모든 요소 쌍이 비교할 수있는 부분 순서 집합입니다. $ a, b \ in S $ 요소는 $ a \ le b $ 또는 $ b \ le a $가 유지되는 경우 비교 가능하다고합니다. Trichotomy 법칙은이 총 주문 세트를 정의합니다. 완전히 정렬 된 집합은 집합 S에서 a와 b의 모든 값에 대해 $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ 속성을 갖는 분산 격자로 정의 할 수 있습니다.
예
\ subseteq에 의해 정렬 된 $ \ lbrace a, b \ rbrace $의 powerset은 전원 집합 $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \의 모든 요소로 완전히 정렬 된 집합입니다. lbrace a, b \ rbrace \ rbrace $는 비슷합니다.
비 합계 주문 세트의 예
작업 x에서 $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ 집합은 y를 전체 순서 집합이 아닙니다.
여기에서 모든 $ (x, y) \ in S, x | y $가 유지되어야하지만 사실이 아닙니다. 2 | 3, 2는 3을 나누지 않기 때문에 3은 2를 나누지 않습니다. 따라서 그것은 총 주문 세트가 아닙니다.
격자
격자는 $ \ lbrace a, b \ rbrace \ in L $ 쌍이 최소 상한 ($ a \ lor b $로 표시)과 최대 하한 ()을 갖는 포셋 $ (L, \ le) $입니다. $ a \ land b $로 표시). LUB $ (\ lbrace a, b \ rbrace) $는 a와 b의 조인이라고합니다. GLB $ (\ lbrace a, b \ rbrace) $는 a와 b의 만남이라고합니다.
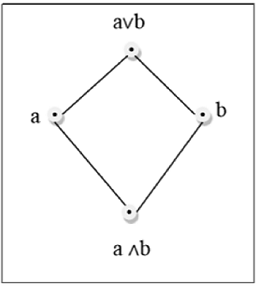
예
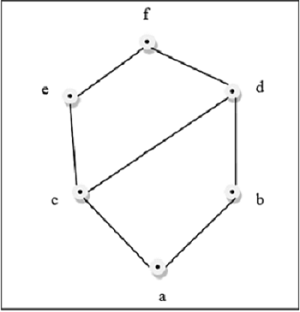
위의 그림은 모든 쌍 $ \ lbrace a, b \ rbrace \ in L $에 대해 GLB와 LUB가 존재하기 때문에 격자입니다.
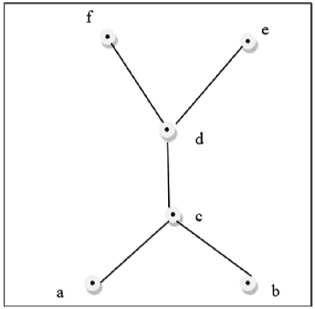
$ GLB (a, b) $ 및 $ LUB (e, f) $가 존재하지 않기 때문에 위의 그림은 격자가 아닙니다.
다른 격자는 아래에서 설명합니다.
경계 격자
격자 L은 요소 1이 가장 크고 요소 0이 가장 적 으면 경계 격자가됩니다.
보완 격자
격자 L은 경계 격자이고 격자의 모든 요소에 보수가있는 경우 보완 격자가됩니다. $ \ exists x (x \ land x '= 0 및 x \ lor x'= 1) $ 인 경우 요소 x에는 보수 x '가 있습니다.
분배 격자
격자가 다음 두 가지 분포 속성을 만족하는 경우이를 분산 격자라고합니다.
$ a \ lor (b \ land c) = (a \ lor b) \ land (a \ lor c) $
$ a \ land (b \ lor c) = (a \ land b) \ lor (a \ land c) $
모듈러 격자
격자가 다음 속성을 만족하면 모듈러 격자라고합니다.
$ a \ land (b \ lor (a \ land d)) = (a \ land b) \ lor (a \ land d) $
격자의 속성
멱 등성 속성
$ a \ 또는 a = a $
$ a \ land a = a $
흡수 속성
$ a \ lor (a \ land b) = a $
$ a \ land (a \ lor b) = a $
교환 속성
$ a \ lor b = b \ lor a $
$ a \ land b = b \ land a $
연관 속성
$ a \ lor (b \ lor c) = (a \ lor b) \ lor c $
$ a \ land (b \ land c) = (a \ land b) \ land c $
격자의 이중
격자의 이중은 '$ \ lor $'와 '$ \ land $'연산을 교환하여 얻습니다.
예
$ \ lbrack a \ lor (b \ land c) \ rbrack \의 이중은 \ \ lbrack a \ land (b \ lor c) \ rbrack $입니다.