그래프 및 그래프 모델
이전 부분에서는 추론, 교정 및 문제 해결을위한 다양한 도구를 소개했습니다. 이 부분에서는 많은 실제 문제를 공식화하는 기초를 형성하는 이산 구조를 연구합니다.
우리가 다룰 두 개의 개별 구조는 그래프와 나무입니다. 그래프는 노드 또는 꼭지점이라고하는 점 집합으로, 가장자리라고하는 선 집합으로 상호 연결됩니다. 그래프 연구 또는graph theory 수학, 공학 및 컴퓨터 과학 분야의 여러 분야에서 중요한 부분입니다.
그래프 란?
Definition − 그래프 ($ G = (V, E) $로 표시)는 비어 있지 않은 정점 또는 노드 V 세트와 모서리 E 세트로 구성됩니다.
Example − 그래프는 $ G = (V, E) $이고 $ V = \ lbrace a, b, c, d \ rbrace $ 및 $ E = \ lbrace \ lbrace a, b \ rbrace, \ lbrace a , c \ rbrace, \ lbrace b, c \ rbrace, \ lbrace c, d \ rbrace \ rbrace $

Degree of a Vertex − 그래프 G의 꼭지점 V의 각도 (도 (V)로 표시)는 꼭지점 V에 입사하는 가장자리의 수입니다.
| 꼭지점 | 정도 | 홀수 |
|---|---|---|
| ㅏ | 2 | 조차 |
| 비 | 2 | 조차 |
| 씨 | 삼 | 이상한 |
| 디 | 1 | 이상한 |
Even and Odd Vertex -꼭지점이 짝수이면 짝수 꼭지점이라고하고, 꼭지점이 홀수이면 꼭지점을 홀수 꼭지점이라고합니다.
Degree of a Graph− 그래프의 차수는 해당 그래프의 가장 큰 정점 차수입니다. 위의 그래프에서 그래프의 정도는 3입니다.
The Handshaking Lemma − 그래프에서 모든 정점의 모든 각도의 합은 가장자리 수의 두 배와 같습니다.
그래프 유형
다양한 유형의 그래프가 있으며 다음 섹션에서 배울 것입니다.
널 그래프
널 그래프에는 간선이 없습니다. $ n $ 정점의 널 그래프는 $ N_n $로 표시됩니다.

간단한 그래프
그래프가 방향이없고 루프 나 다중 간선이 포함되지 않은 경우 그래프를 단순 그래프 / 엄격 그래프라고합니다.

멀티 그래프
그래프에서 동일한 꼭지점 집합 사이에 여러 모서리가 허용되는 경우이를 Multigraph라고합니다. 즉, 적어도 하나의 루프 또는 다중 에지가있는 그래프입니다.

유 방향 및 무 방향 그래프
그래프 $ G = (V, E) $는 에지 세트가 순서가 지정된 정점 쌍으로 구성된 경우 유 방향 그래프라고하고 에지 세트가 순서가 지정되지 않은 정점 쌍으로 구성된 경우 그래프는 무 방향이라고합니다.


연결 및 연결 해제 그래프
그래프의 두 꼭지점이 경로로 연결된 경우 그래프가 연결됩니다. 그래프의 두 꼭지점이 경로로 연결되어 있지 않으면 그래프가 연결 해제됩니다. 그래프 G의 연결이 끊어지면 $ G $의 모든 최대 연결 하위 그래프를 그래프 $ G $의 연결된 구성 요소라고합니다.


일반 그래프
그래프의 모든 꼭지점이 같은 정도이면 그래프는 규칙적입니다. $ r $ 정도의 정규 그래프 G에서 $ G $의 각 꼭지점의 정도는 r입니다.

완전한 그래프
모든 두 꼭지점 쌍이 정확히 하나의 모서리로 결합되는 경우 그래프를 완전한 그래프라고합니다. n 개의 정점이있는 전체 그래프는 $ K_n $로 표시됩니다.
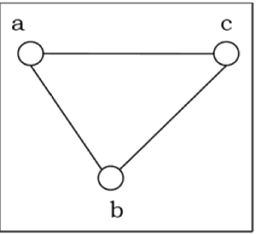
사이클 그래프
그래프가 단일 사이클로 구성된 경우이를 사이클 그래프라고합니다. n 개의 정점이있는 순환 그래프는 $ C_n $로 표시됩니다.

이분 그래프
그래프 G의 꼭지점 집합이 $ V_1 $ 및 $ V_2 $라는 두 개의 분리 된 집합으로 분할 될 수있는 경우 그래프의 각 모서리가 $ V_1 $의 꼭지점을 $ V_2 $의 꼭지점에 연결하는 방식으로, G에는 $ V_1 $의 두 정점 또는 $ V_2 $의 두 정점을 연결하는 간선이 없습니다. 그러면 $ G $ 그래프를 이분 그래프라고합니다.

완전한 이분 그래프
완전한 이분 그래프는 첫 번째 세트의 각 정점이 두 번째 세트의 모든 단일 정점에 결합되는 이분 그래프입니다. 완전한 이분 그래프는 $ K_ {x, y} $로 표시됩니다. 여기서 그래프 $ G $에는 첫 번째 세트의 $ x $ 정점과 두 번째 세트의 $ y $ 정점이 포함됩니다.

그래프 표현
주로 그래프를 표현하는 두 가지 방법이 있습니다.
- 인접 행렬
- 인접 목록
인접 행렬
인접 행렬 $ A [V] [V] $는 $ V \ times V $ 크기의 2D 배열입니다. 여기서 $ V $는 무 방향 그래프의 꼭지점 수입니다. $ V_x $에서 $ V_y $ 사이에 가장자리가 있으면 $ A [V_x] [V_y] = 1 $ 및 $ A [V_y] [V_x] = 1 $의 값이 있고 그렇지 않으면 값은 0이됩니다. 유 방향 그래프의 경우 $ V_x $에서 $ V_y $ 사이에 간선이 있으면 $ A [V_x] [V_y] = 1 $의 값이되고 그렇지 않으면 값은 0이됩니다.
Adjacency Matrix of an Undirected Graph
다음 무 방향 그래프를 고려하고 인접 행렬을 구성 해 보겠습니다.

위의 무 방향 그래프의 인접 행렬은-
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
1 |
0 |
1 |
0 |
c |
1 |
1 |
0 |
1 |
d |
0 |
0 |
1 |
0 |
Adjacency Matrix of a Directed Graph
다음의 유향 그래프를 고려하고 인접 행렬을 구성 해 보겠습니다.

위 방향 그래프의 인접 행렬은 다음과 같습니다.
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
0 |
0 |
1 |
0 |
c |
0 |
0 |
0 |
1 |
d |
0 |
0 |
0 |
0 |
인접 목록
인접 목록에서 연결 목록의 배열 $ (A [V]) $는 $ V $ 개수의 꼭지점으로 그래프 G를 나타내는 데 사용됩니다. $ A [V_x] $ 항목은 $ Vx-th $ 정점에 인접한 정점의 링크 된 목록을 나타냅니다. 무 방향 그래프의 인접 목록은 아래 그림과 같습니다.

평면형 vs. 비 평면형 그래프
Planar graph− 그래프 $ G $는 모서리가 교차하지 않고 평면에 그릴 수있는 경우 평면 그래프라고합니다. 모서리 교차가없는 평면에 그래프를 그리면 평면에 그래프를 삽입하는 것을 말합니다.

Non-planar graph − 그래프 모서리가 교차하지 않는 평면에 그릴 수없는 그래프는 비평면입니다.

동형
두 그래프 G와 H에 동일한 방식으로 연결된 동일한 수의 꼭지점이 포함되어있는 경우 동형 그래프라고합니다 ($ G \ cong H $로 표시).
동형보다 비 동형을 확인하는 것이 더 쉽습니다. 다음 조건 중 하나가 발생하면 두 그래프가 비 동형이됩니다.
- 연결된 구성 요소의 수가 다릅니다
- 정점 설정 카디널리티가 다릅니다.
- 에지 세트 카디널리티가 다릅니다.
- 학위 순서가 다릅니다.
예
다음 그래프는 동형입니다-
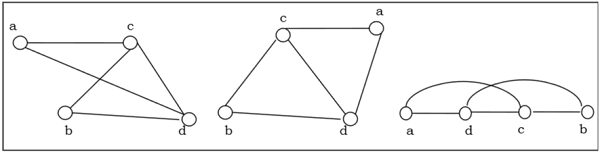
동형
그래프 $ G $에서 그래프 $ H $ 로의 동형은 매핑입니다 (양측 사 매핑이 아닐 수도 있음) $ h : G \ rightarrow H $ 다음과 같음 − $ (x, y) \ in E (G) \ rightarrow (h (x), h (y)) \ in E (H) $. 그래프 $ G $의 인접 정점을 그래프 $ H $의 인접 정점에 매핑합니다.
동형의 속성
동형은 bijective 매핑 인 경우 동형입니다.
동형은 항상 그래프의 가장자리와 연결성을 유지합니다.
동형의 구성도 동형입니다.
다른 그래프의 동형 그래프가 있는지 확인하는 것은 NPcomplete 문제입니다.
오일러 그래프
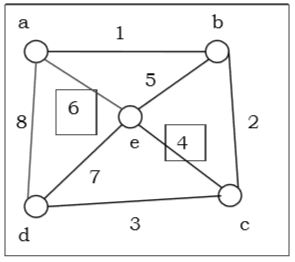
연결된 그래프 $ G $는 그래프 $ G $의 모든 모서리를 포함하는 닫힌 트레일이있는 경우 오일러 그래프라고합니다. 오일러 경로는 그래프의 모든 모서리를 정확히 한 번 사용하는 경로입니다. 오일러 경로는 다른 정점에서 시작하고 끝납니다.
오일러 회로는 그래프의 모든 모서리를 정확히 한 번 사용하는 회로입니다. 오일러 회로는 항상 동일한 정점에서 시작하고 끝납니다. 연결된 그래프 $ G $는 $ G $의 모든 정점이 짝수 인 경우에만 오일러 그래프이고, 연결된 그래프 $ G $는 에지 세트가 사이클로 분해 될 수있는 경우에만 오일러 그래프입니다.

위 그래프는 오일러 그래프로 $“a \ : 1 \ : b \ : 2 \ : c \ : 3 \ : d \ : 4 \ : e \ : 5 \ : c \ : 6 \ : f \ : 7 \ : g”$는 그래프의 모든 모서리를 포함합니다.

해밀턴 그래프
$ G $의 모든 정점을 포함하는주기가있는 경우 연결된 그래프 $ G $를 Hamiltonian 그래프라고하고 그주기를 Hamiltonian주기라고합니다. 그래프 $ G $의 Hamiltonian Walk는 각 정점을 정확히 한 번 통과하는 산책입니다.
$ G $가 n 개의 정점이있는 단순한 그래프 인 경우 $ n \ geq 3 $ $ deg (v) \ geq \ frac {n} {2} $가 각 정점 $ v $에 대해 $ G $는 다음과 같습니다. 해밀턴 그래프. 이것은 ... 불리운다Dirac's Theorem.
$ G $가 $ n $ 정점이있는 간단한 그래프이고 $ deg (x) + deg (y) \ geq n $이면 인접하지 않은 정점 x와 y의 각 쌍에 대해 $ n \ geq 2 $이면 그래프 $ G $는 해밀턴 그래프입니다. 이것은 ... 불리운다Ore's theorem.