이산 수학-관계
세트에 대해 논의 할 때마다 세트 요소 간의 관계가 다음으로 나타납니다. Relations 동일한 세트의 객체 사이 또는 둘 이상의 세트의 객체 사이에 존재할 수 있습니다.
정의 및 속성
세트 x에서 y까지의 이진 관계 R ($ xRy $ 또는 $ R (x, y) $로 작성 됨)은 데카르트 곱 $ x \ x y $의 하위 집합입니다. 순서가 지정된 G 쌍이 반대로되면 관계도 변경됩니다.
일반적으로 세트 $ A_1, \ dots, \ 및 \ A_n $ 사이의 n 진 관계 R은 n 진 곱 $ A_1 \ x \ dots \ x A_n $의 서브 세트입니다. 관계 R의 최소 카디널리티는 0이고이 경우 최대 값은 $ n ^ 2 $입니다.
단일 집합 A의 이진 관계 R은 $ A \ x A $의 하위 집합입니다.
각각 카디널리티가 m 및 n 인 두 개의 별개 세트 A와 B의 경우 A에서 B까지 관계 R의 최대 카디널리티는 mn 입니다.
도메인 및 범위
두 세트 A와 B가 있고 관계 R에 순서 쌍 (x, y)이 있으면-
그만큼 domainR의 Dom (R)은 $ \ lbrace x \ : | \ : (x, y) \ in R \ : for \ : some \ : y \ : in \ : B \ rbrace $
그만큼 range R의 Ran (R)은 $ \ lbrace y \ : | \ : (x, y) \ in R \ : for \ : some \ : x \ : in \ : A \ rbrace $입니다.
예
$ A = \ lbrace 1, 2, 9 \ rbrace $ 및 $ B = \ lbrace 1, 3, 7 \ rbrace $
사례 1 − 관계 R이 '같음'이면 $ R = \ lbrace (1, 1), (3, 3) \ rbrace $
Dom (R) = $ \ lbrace 1, 3 \ rbrace, Ran (R) = \ lbrace 1, 3 \ rbrace $
사례 2 − 관계 R이 '보다 작 으면'$ R = \ lbrace (1, 3), (1, 7), (2, 3), (2, 7) \ rbrace $
Dom (R) = $ \ lbrace 1, 2 \ rbrace, Ran (R) = \ lbrace 3, 7 \ rbrace $
사례 3 − 관계 R이 '보다 큼'이면 $ R = \ lbrace (2, 1), (9, 1), (9, 3), (9, 7) \ rbrace $
Dom (R) = $ \ lbrace 2, 9 \ rbrace, Ran (R) = \ lbrace 1, 3, 7 \ rbrace $
그래프를 이용한 관계 표현
관계는 유 방향 그래프를 사용하여 나타낼 수 있습니다.
그래프의 정점 수는 관계가 정의 된 집합의 요소 수와 같습니다. 관계 R의 각 순서 쌍 (x, y)에 대해 꼭지점 'x'에서 꼭지점 'y'로 향하는 가장자리가 있습니다. 정렬 된 쌍 (x, x)이 있으면 꼭지점 'x'에 자체 루프가 있습니다.
$ R = \ lbrace (1, 1), (1,2), (3, 2) \ rbrace $ on set $ S = \ lbrace 1, 2, 3 \ rbrace $에 관계가 있다고 가정합니다. 다음 그래프로 표현-
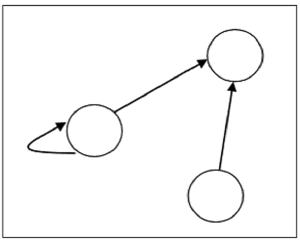
관계 유형
그만큼 Empty Relation 세트 X와 Y 사이 또는 E에서 빈 세트 $ \ emptyset $
그만큼 Full Relation 세트 X와 Y 사이는 세트 $ X \ x Y $
그만큼 Identity Relation세트 X는 세트 $ \ lbrace (x, x) | x \ in X \ rbrace $
관계 R의 역 관계 R '은 다음과 같이 정의됩니다. − $ R'= \ lbrace (b, a) | (a, b) \ in R \ rbrace $
Example − $ R = \ lbrace (1, 2), (2, 3) \ rbrace $이면 $ R '$는 $ \ lbrace (2, 1), (3, 2) \ rbrace $가됩니다.
세트 A의 관계 R이 호출됩니다. Reflexive $ \ forall a \ in A $가 a (aRa hold)와 관련된 경우
Example − 관계식 $ R = \ lbrace (a, a), (b, b) \ rbrace $ on set $ X = \ lbrace a, b \ rbrace $ is reflexive.
세트 A의 관계 R이 호출됩니다. Irreflexive $ a \ in A $가 a와 관련이없는 경우 (aRa는 보유하지 않음).
Example − 관계식 $ R = \ lbrace (a, b), (b, a) \ rbrace $ on set $ X = \ lbrace a, b \ rbrace $ is irreflexive.
세트 A의 관계 R이 호출됩니다. Symmetric $ xRy $가 $ yRx $, $ \ forall x \ in A $ 및 $ \ forall y \ in A $를 의미하는 경우.
Example − 관계식 $ R = \ lbrace (1, 2), (2, 1), (3, 2), (2, 3) \ rbrace $ on set $ A = \ lbrace 1, 2, 3 \ rbrace $ is 대칭.
세트 A의 관계 R이 호출됩니다. Anti-Symmetric $ xRy $ 및 $ yRx $가 $ x = y \ : \ forall x \ in A $ 및 $ \ forall y \ in A $를 의미하는 경우.
Example − 관계 $ R = \ lbrace (x, y) \ to N | \ : x \ leq y \ rbrace $는 $ x \ leq y $ 및 $ y \ leq x $가 $ x = y $를 의미하므로 반대 칭입니다. .
세트 A의 관계 R이 호출됩니다. Transitive $ xRy $ 및 $ yRz $가 $ xRz, \ forall x, y, z \ in A $를 의미하는 경우.
Example − $ R = \ lbrace (1, 2), (2, 3), (1, 3) \ rbrace $ on set $ A = \ lbrace 1, 2, 3 \ rbrace $는 전 이적입니다.
관계는 Equivalence Relation 반사적이고 대칭 적이며 전 이적이라면.
Example − 관계 $ R = \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \ rbrace $ on set $ A = \ lbrace 1, 2, 3 \ rbrace $는 재귀적이고 대칭 적이며 전이 적이므로 등가 관계입니다.