이산 수학-세트

독일 수학자 G. Cantor세트의 개념을 도입했습니다. 그는 특정 규칙이나 설명에 의해 선택된 명확하고 구별 가능한 개체의 모음으로 집합을 정의했습니다.

Set이론은 계수 이론, 관계, 그래프 이론 및 유한 상태 기계와 같은 여러 다른 연구 분야의 기초를 형성합니다. 이 장에서 우리는Set Theory.

세트-정의

집합은 다른 요소의 정렬되지 않은 컬렉션입니다. 집합 대괄호를 사용하여 요소를 나열하여 집합을 명시 적으로 작성할 수 있습니다. 요소의 순서가 변경되거나 집합의 요소가 반복되면 집합에서 변경되지 않습니다.

세트의 몇 가지 예

모든 양의 정수 세트
태양계에있는 모든 행성의 집합
인도의 모든 주 세트
알파벳의 모든 소문자 집합

세트의 표현

세트는 두 가지 방법으로 표현할 수 있습니다.

명단 또는 표 형식
빌더 표기법 설정

명단 또는 표 형식

세트는이를 구성하는 모든 요소를 나열하여 표시됩니다. 요소는 중괄호로 묶여 있으며 쉼표로 구분됩니다.

Example 1 − 영어 알파벳 모음 세트, $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 − 10보다 작은 홀수 세트, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

빌더 표기법 설정

집합은 집합의 요소가 공통으로 갖는 속성을 지정하여 정의됩니다. 집합은 $ A = \ lbrace x : p (x) \ rbrace $로 설명됩니다.

Example 1 − $ \ lbrace a, e, i, o, u \ rbrace $ 세트는 −

$ A = \ lbrace x : \ text {x는 영어 알파벳 모음} \ rbrace $

Example 2 − $ \ lbrace 1,3,5,7,9 \ rbrace $ 세트는 −

$ B = \ l 중괄호 x : 1 \ le x \ lt 10 \ 및 \ (x \ % 2) \ ne 0 \ rbrace $

요소 x가 집합 S의 구성원이면 $ x \ in S $로 표시되고 요소 y가 집합 S의 구성원이 아니면 $ y \ notin S $로 표시됩니다.

Example− $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $이지만 $ 1.5 \ notin S $

몇 가지 중요한 세트

N − 모든 자연수 집합 = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z − 모든 정수 세트 = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ − 모든 양의 정수 집합

Q − 모든 유리수의 집합

R − 모든 실수의 집합

W − 모든 정수의 집합

세트의 카디널리티

$ | S | $로 표시되는 집합 S의 카디널리티는 집합의 요소 수입니다. 이 번호는 기본 번호라고도합니다. 집합에 무한한 수의 요소가있는 경우 카디널리티는 $ \ infty $입니다.

Example− $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ l 중괄호 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $

X와 Y의 두 세트가 있으면

$ | X | = | Y | $는 동일한 카디널리티를 갖는 두 세트 X 및 Y를 나타냅니다. X의 원소 개수가 Y의 원소 개수와 정확히 같을 때 발생합니다.이 경우 X에서 Y까지의 bijective 함수 'f'가 있습니다.
$ | X | \ le | Y | $는 집합 X의 카디널리티가 집합 Y의 카디널리티보다 작거나 같음을 나타냅니다. X의 원소 개수가 Y보다 작거나 같을 때 발생합니다. 여기에는 X에서 Y까지의 주입 함수 'f'가 있습니다.
$ | X | \ lt | Y | $는 세트 X의 카디널리티가 세트 Y의 카디널리티보다 작음을 나타냅니다. X의 원소 개수가 Y의 개수보다 적을 때 발생합니다. 여기서 X에서 Y까지의 함수 'f'는 주입 기능이지만 bijective는 아닙니다.
$ If \ | X | \ le | Y | $ 및 $ | X | \ ge | Y | $ 다음에 $ | X | = | Y | $. 집합 X와 Y는 일반적으로 동등한 집합이라고합니다.

세트의 종류

세트는 여러 유형으로 분류 할 수 있습니다. 그중 일부는 유한, 무한, 하위 집합, 범용, 적절한, 단일 집합 등입니다.

유한 세트

한정된 수의 요소를 포함하는 집합을 유한 집합이라고합니다.

Example− $ S = \ l 중괄호 x \ : | \ : x \ in N $ 및 $ 70 \ gt x \ gt 50 \ rbrace $

무한 세트

무한한 수의 요소를 포함하는 집합을 무한 집합이라고합니다.

Example− $ S = \ l 중괄호 x \ : | \ : x \ in N $ 및 $ x \ gt 10 \ rbrace $

부분 집합

X의 모든 요소가 집합 Y의 요소 인 경우 집합 X는 집합 Y ($ X \ subseteq Y $로 기록됨)의 하위 집합입니다.

Example 1− $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ 및 $ Y = \ lbrace 1, 2 \ rbrace $. 여기서 집합 Y는 집합 Y의 모든 요소가 집합 X에 있으므로 집합 X의 하위 집합입니다. 따라서 $ Y \ subseteq X $를 쓸 수 있습니다.

Example 2− $ X = \ lbrace 1, 2, 3 \ rbrace $ 및 $ Y = \ lbrace 1, 2, 3 \ rbrace $. 여기서 집합 Y는 집합 Y의 모든 요소가 집합 X에 있으므로 집합 X의 부분 집합 (적절한 부분 집합이 아님)입니다. 따라서 $ Y \ subseteq X $를 작성할 수 있습니다.

적절한 하위 집합

용어 "적절한 부분 집합"은 "부분 집합이지만 같지 않은 부분 집합"으로 정의 할 수 있습니다. X의 모든 요소가 집합 Y 및 $ | X |의 요소 인 경우 집합 X는 집합 Y의 적절한 하위 집합입니다 ($ X \ subset Y $로 기록됨). \ lt | Y | $.

Example− $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ 및 $ Y = \ lbrace 1, 2 \ rbrace $. $ Y $의 모든 요소가 $ X $에도 포함되어 있고 $ X $에 $ Y $보다 많은 요소가 하나 이상 있으므로 $ Y \ subset X $를 설정합니다.

유니버설 세트

특정 컨텍스트 또는 애플리케이션에있는 모든 요소의 모음입니다. 해당 컨텍스트 또는 응용 프로그램의 모든 집합은 본질적으로이 범용 집합의 하위 집합입니다. 유니버설 세트는 $ U $로 표시됩니다.

Example− $ U $는 지구상의 모든 동물의 집합으로 정의 할 수 있습니다. 이 경우 모든 포유류의 집합은 $ U $의 하위 집합이고, 모든 물고기 집합은 $ U $의 하위 집합이며, 모든 곤충 집합은 $ U $의 하위 집합입니다.

빈 세트 또는 널 세트

빈 세트에는 요소가 없습니다. $ \ emptyset $로 표시됩니다. 빈 집합의 요소 수가 유한하므로 빈 집합은 유한 집합입니다. 빈 세트 또는 널 세트의 카디널리티는 0입니다.

Example− $ S = \ l 중괄호 x \ : | \ : x \ in N $ 및 $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

싱글 톤 세트 또는 단위 세트

싱글 톤 세트 또는 단위 세트에는 하나의 요소 만 포함됩니다. 싱글 톤 세트는 $ \ lbrace s \ rbrace $로 표시됩니다.

Example− $ S = \ l 중괄호 x \ : | \ : x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

동일 세트

두 세트에 동일한 요소가 포함되어 있으면 동일하다고합니다.

Example − $ A = \ lbrace 1, 2, 6 \ rbrace $ 및 $ B = \ lbrace 6, 1, 2 \ rbrace $이면 집합 A의 모든 요소가 집합 B의 요소이고 집합의 모든 요소이므로 동일합니다. B는 집합 A의 요소입니다.

동등한 세트

두 세트의 카디널리티가 동일하면 동등한 세트라고합니다.

Example− $ A = \ lbrace 1, 2, 6 \ rbrace $ 및 $ B = \ lbrace 16, 17, 22 \ rbrace $이면 A의 카디널리티가 B의 카디널리티와 같기 때문에 동일합니다. 즉 $ | A | = | B | = 3 달러

겹치는 세트

하나 이상의 공통 요소가있는 두 세트를 중첩 세트라고합니다.

세트가 겹치는 경우 −

$ n (A \ 컵 B) = n (A) + n (B)-n (A \ 캡 B) $
$ n (A \ 컵 B) = n (A-B) + n (B-A) + n (A \ 캡 B) $
$ n (A) = n (A-B) + n (A \ cap B) $
$ n (B) = n (B-A) + n (A \ cap B) $

Example− $ A = \ lbrace 1, 2, 6 \ rbrace $ 및 $ B = \ lbrace 6, 12, 42 \ rbrace $. 공통 요소 '6'이 있으므로이 세트는 겹치는 세트입니다.

분리 된 세트

두 세트 A와 B는 공통 요소가 하나도없는 경우 분리 세트라고합니다. 따라서 분리 된 집합은 다음과 같은 속성을 갖습니다.

$ n (A \ cap B) = \ emptyset $
$ n (A \ 컵 B) = n (A) + n (B) $

Example − Let, $ A = \ lbrace 1, 2, 6 \ rbrace $ and $ B = \ lbrace 7, 9, 14 \ rbrace $, 단일 공통 요소가 없으므로 이러한 집합은 겹치는 집합입니다.

벤 다이어그램

1880 년 John Venn이 발명 한 벤 다이어그램은 다른 수학적 세트 간의 가능한 모든 논리적 관계를 보여주는 개략도입니다.

Examples

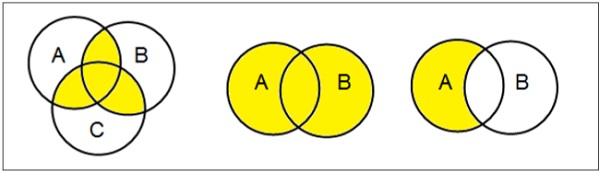
작업 설정

집합 연산에는 집합 합집합, 집합 교차, 집합 차이, 집합 보완 및 카티 전 곱이 포함됩니다.

조합 설정

집합 A와 B의 합집합 ($ A \ cup B $로 표시)은 A, B 또는 A와 B 모두에있는 요소 집합입니다. 따라서 $ A \ cup B = \ lbrace x \ : | \ : x \ in A \ OR \ x \ in B \ rbrace $.

Example− $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ 및 B = $ \ lbrace 13, 14, 15 \ rbrace $, $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (공통 요소는 한 번만 발생)

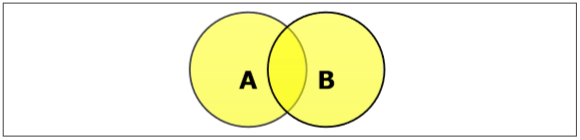
교차로 설정

집합 A와 B의 교차점 ($ A \ cap B $로 표시)은 A와 B 모두에있는 요소 집합입니다. 따라서 $ A \ cap B = \ lbrace x \ : | \ : x \ in A \ AND \ x \ in B \ rbrace $.

Example − $ A = \ lbrace 11, 12, 13 \ rbrace $ 및 $ B = \ lbrace 13, 14, 15 \ rbrace $이면 $ A \ cap B = \ lbrace 13 \ rbrace $.

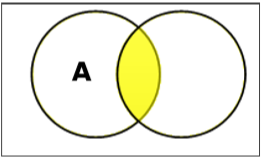
차이 / 상대 보완 설정

집합 A와 B의 집합 차이 ($ A – B $로 표시)는 A에만 있지만 B에는없는 요소 집합입니다. 따라서 $ A-B = \ lbrace x \ : | \ : x \ in A \ AND \ x \ notin B \ rbrace $.

Example− $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ 및 $ B = \ lbrace 13, 14, 15 \ rbrace $이면 $ (A-B) = \ lbrace 10, 11, 12 \ rbrace $ 및 $ (B-A) = \ lbrace 14, 15 \ rbrace $. 여기에서 $ (A-B) \ ne (B-A) $를 볼 수 있습니다.

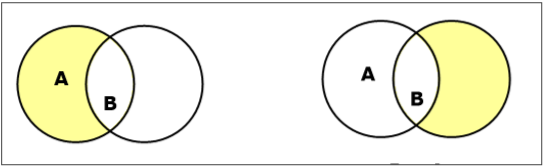
세트의 보완

집합 A의 보완 ($ A '$로 표시)은 집합 A에없는 요소 집합입니다. 따라서 $ A'= \ lbrace x | x \ notin A \ rbrace $.

보다 구체적으로 $ A '= (U-A) $ 여기서 $ U $는 모든 개체를 포함하는 범용 집합입니다.

Example− $ A = \ lbrace x \ : | \ : x \ \ : {belongs \ : to \ : set \ : of \ : odd \ : integers} \ rbrace $ then $ A '= \ lbrace y \ : | \ : y \ \ : {does \ : not \ : 소속 \ : to \ : set \ : of \ : odd \ : 정수} \ rbrace $

데카르트 곱 / 외적

$ A_1 \ times A_2 \ dots \ times A_n $로 표시된 n 개의 세트 수 $ A_1, A_2, \ dots A_n $의 데카르트 곱은 가능한 모든 순서 쌍 $ (x_1, x_2, \ dots x_n) $로 정의 될 수 있습니다. $ x_1 \ in A_1, x_2 \ in A_2, \ dots x_n \ in A_n $

Example − 만약 우리가 $ A = \ lbrace a, b \ rbrace $ 그리고 $ B = \ lbrace 1, 2 \ rbrace $,

A와 B의 데카르트 곱은 − $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $로 작성됩니다.

B와 A의 데카르트 곱은 다음과 같이 작성됩니다. − $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

파워 세트

집합 S의 거듭 제곱 집합은 빈 집합을 포함하여 S의 모든 하위 집합 집합입니다. 카디널리티 n의 집합 S의 거듭 제곱 집합의 카디널리티는 $ 2 ^ n $입니다. 전력 세트는 $ P (S) $로 표시됩니다.

Example −

$ S = \ lbrace a, b, c, d \ rbrace $의 경우 부분 집합을 계산해 보겠습니다.

0 요소가있는 부분 집합 − $ \ lbrace \ emptyset \ rbrace $ (빈 집합)
요소가 1 개인 부분 집합 − $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
2 개 요소로 구성된 부분 집합 − $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
3 개의 요소가있는 부분 집합 − $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
요소가 4 개인 부분 집합 − $ \ lbrace a, b, c, d \ rbrace $

따라서 $ P (S) = $

$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 달러

Note − 빈 집합의 거듭 제곱 집합도 빈 집합입니다.

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

세트 분할

집합의 분할 (예 : S )은 다음 세 가지 조건을 충족하는 n 개의 분리 된 부분 집합 (예 : $ P_1, P_2, \ dots P_n $ )의 모음입니다.

$ P_i $에 빈 세트가 없습니다.

$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
부분 집합의 합집합은 전체 원본 집합과 같아야합니다.

$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
두 개의 다른 세트의 교차는 비어 있습니다.

$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ 여기서 \ n \ ge a, \ : b \ ge 0 \ rbrack $

Example

$ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

하나의 가능한 분할은 $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $입니다.

또 다른 가능한 분할은 $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $입니다.