이산 수학-그래프에 대한 추가 정보
그래프 채색
그래프 색상은 인접한 정점이 같은 색을 가지지 않도록 그래프 G의 각 정점에 색을 할당하는 절차입니다. 목표는 그래프를 채색하는 동안 색상 수를 최소화하는 것입니다. 그래프 G를 색칠하는 데 필요한 최소 색상 수를 해당 그래프의 색수라고합니다. 그래프 색상 문제는 NP Complete 문제입니다.
그래프를 색칠하는 방법
n 개의 꼭지점으로 그래프 G를 색칠하는 데 필요한 단계는 다음과 같습니다.
Step 1 − 그래프의 정점을 순서대로 정렬합니다.
Step 2 − 첫 번째 정점을 선택하고 첫 번째 색상으로 채색합니다.
Step 3− 다음 정점을 선택하고 인접한 정점에 색상이 지정되지 않은 가장 낮은 번호의 색상으로 색상을 지정합니다. 인접한 모든 정점이이 색상으로 색칠 된 경우 새 색상을 할당합니다. 모든 정점이 색상이 지정 될 때까지이 단계를 반복합니다.
Example
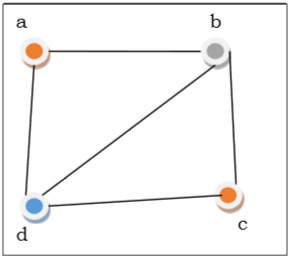
위 그림에서 첫 번째 정점 $ a $는 빨간색으로 표시됩니다. 정점 a의 인접 정점이 다시 인접하므로 정점 $ b $와 정점 $ d $는 각각 다른 색, 녹색 및 파란색으로 채색됩니다. 그러면 $ c $의 인접한 정점이 빨간색으로 표시되지 않으므로 정점 $ c $가 빨간색으로 표시됩니다. 따라서 그래프를 3 색으로 채색 할 수 있습니다. 따라서 그래프의 색수는 3입니다.
그래프 채색의 응용
그래프 채색의 일부 응용 프로그램은 다음과 같습니다.
- 할당 등록
- 지도 색칠
- 이분 그래프 확인
- 모바일 무선 주파수 할당
- 시간표 만들기 등
그래프 순회
그래프 순회는 그래프의 모든 정점을 어떤 체계적인 순서로 방문하는 문제입니다. 주로 그래프를 횡단하는 두 가지 방법이 있습니다.
- 폭 우선 검색
- 깊이 우선 검색
폭 우선 검색
BFS (Breadth First Search)는 그래프 $ G $의 시작 레벨 0 정점 $ X $에서 시작됩니다. 그런 다음 $ X $의 이웃 인 모든 정점을 방문합니다. 방문 후 정점을 "방문 됨"으로 표시하고 레벨 1에 배치합니다. 그런 다음 레벨 1 정점에서 시작하여 모든 레벨 1 정점 등에 동일한 방법을 적용합니다. 그래프의 모든 정점을 방문하면 BFS 순회가 종료됩니다.
BFS Algorithm
개념은 인접 정점의 다른 인접 정점을 방문하기 전에 모든 인접 정점을 방문하는 것입니다.
모든 노드의 상태를 "준비"로 초기화합니다.
소스 정점을 대기열에 넣고 상태를 "대기 중"으로 변경합니다.
대기열이 비워 질 때까지 다음 두 단계를 반복하십시오-
대기열에서 첫 번째 정점을 제거하고 "Visited"로 표시합니다.
상태가 "준비"인 제거 된 정점의 모든 인접 항목을 대기열 뒤쪽에 추가합니다. 상태를 "대기 중"으로 표시하십시오.
Problem
그래프 (소스 정점은 'a'임)를 가져와 BFS 알고리즘을 적용하여 순회 순서를 알아 봅시다.
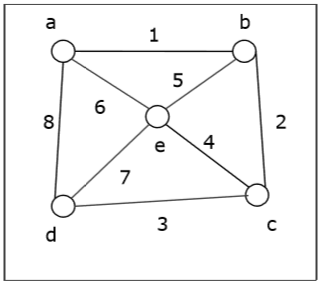
Solution −
모든 정점의 상태를 "준비"로 초기화합니다.
넣어 을 큐에와 "대기"로 상태를 변경합니다.
대기열에서 제거 하고 "방문 됨"으로 표시합니다.
추가 "준비"상태에서의 이웃 B, D 및 E 큐의 끝과 '대기'상태로 표시 할 수 있습니다.
대기열에서 b 를 제거 하고 "방문 됨"으로 표시하고 "준비"이웃 c 를 대기열 끝에두고 c 를 "대기"로 표시 합니다.
대기열에서 d 를 제거 하고 "방문 됨"으로 표시합니다. "준비"상태의 이웃이 없습니다.
대기열에서 e 를 제거 하고 "방문 됨"으로 표시합니다. "준비"상태의 이웃이 없습니다.
대기열에서 c 를 제거 하고 "방문 됨"으로 표시합니다. "준비"상태의 이웃이 없습니다.
대기열이 비어 있으므로 중지하십시오.
그래서 순회 순서는-
$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $
순회의 대체 순서는 다음과 같습니다.
$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
또는 $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $
또는 $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $
또는 $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
또는 $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Application of BFS
- 최단 경로 찾기
- 가중치가없는 그래프에 대한 최소 스패닝 트리
- GPS 내비게이션 시스템
- 무 방향 그래프에서주기 감지
- 하나의 연결된 구성 요소 내에서 모든 노드 찾기
Complexity Analysis
$ G (V, E) $를 $ | V | $ 정점 수와 $ | E | $ 모서리 수를 갖는 그래프라고합시다. 폭 우선 검색 알고리즘이 그래프의 모든 정점을 방문하고 모든 에지를 확인하면 시간 복잡도는 다음과 같습니다.
$$ O (| V | + | E |). O (| E |) $$
$ O (1) $와 $ O (| V2 |) $ 사이에서 다를 수 있습니다.
깊이 우선 검색
DFS (Depth First Search) 알고리즘은 정점 $ v $에서 시작하여 이전에 방문한 적이없는 인접 정점 (예 : x)으로 이동하여 "방문 됨"으로 표시하고 인접 정점 $ x $로 계속 진행합니다. 곧.
임의의 정점에서 인접한 모든 정점을 방문한 경우 이전에 통과하지 않은 인접 정점이있는 첫 번째 정점을 찾을 때까지 역 추적합니다. 그런 다음 해당 정점을 횡단하고 방문한 모든 정점을 횡단하고 다시 역 추적해야 할 때까지 인접한 정점을 계속합니다. 이런 식으로 초기 정점 $ v $에서 도달 할 수있는 모든 정점을 횡단합니다.
DFS Algorithm
개념은 다른 인접 정점을 방문하기 전에 인접 정점의 모든 인접 정점을 방문하는 것입니다.
모든 노드의 상태를 "준비"로 초기화
소스 정점을 스택에 넣고 상태를 "대기"로 변경합니다.
스택이 비워 질 때까지 다음 두 단계를 반복하십시오.
스택에서 상단 정점을 꺼내 "Visited"로 표시합니다.
상태가 "준비"인 제거 된 정점의 모든 인접 항목을 스택 맨 위로 밉니다. 상태를 "대기 중"으로 표시하십시오.
Problem
그래프 (소스 정점은 'a')를 가져 와서 순회 순서를 알아 내기 위해 DFS 알고리즘을 적용 해 보겠습니다.
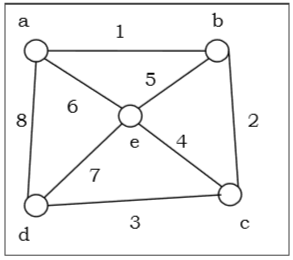
Solution
모든 정점의 상태를 "준비"로 초기화합니다.
밀어 을 스택 및 "대기"로 상태를 변경합니다.
팝 을 하고 "방문"로 표시합니다.
밀어 "준비"상태에서의 이웃 전자, D 와 B 스택 맨과 "대기"로 표시합니다.
팝 (B)을 , 스택에서의 "준비"이웃 푸시 "방문"로 표시 C가 스택에.
팝 C를 스택에서 그것은 "방문"로 표시합니다. "준비된"이웃이 없습니다.
팝 D를 스택에서 그것을 "방문"로 표시한다. "준비된"이웃이 없습니다.
팝 전자 스택에서 그것은 "방문"로 표시합니다. "준비된"이웃이 없습니다.
스택이 비어 있습니다. 그러니 그만해
그래서 순회 순서는-
$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $
순회의 대체 순서는 다음과 같습니다.
$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $
또는 $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $
또는 $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
또는 $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $
또는 $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $
Complexity Analysis
$ G (V, E) $를 $ | V | $ 정점 수와 $ | E | $ 모서리 수를 갖는 그래프라고합시다. DFS 알고리즘이 그래프의 모든 정점을 방문하고 모든 에지를 확인하면 시간 복잡도는 다음과 같습니다.
$$ \ 원형 대시 (| V | + | E |) $$
Applications
- 그래프에서주기 감지
- 토폴로지 정렬을 찾으려면
- 그래프가 2 분할인지 테스트하려면
- 연결된 구성 요소 찾기
- 그래프의 다리 찾기
- 그래프에서 이중 연결 찾기
- Knight 's Tour 문제 해결
- 단 하나의 솔루션으로 퍼즐 풀기