적성-기하학
포인트
점은 정확한 위치입니다.
라인 세그먼트
두 지점 A와 B 사이의 직선 경로를 선분 AB라고합니다. 선분에는 두 개의 끝 점이 있습니다.

레이
선분 AB를 한 방향으로 무기한 연장하면 광선 AB를 얻습니다. Ray AB에는 A라는 하나의 끝 점이 있습니다.

선
양방향으로 무한히 연장 된 선분 AB를 선 AB라고합니다.

선은 무한히 많은 점을 포함합니다.
주어진 점을 통해 무한히 많은 선을 그릴 수 있습니다.
주어진 두 점 A와 B를 통과하기 위해 하나의 선만 그릴 수 있습니다.
두 선이 한 지점에서 만납니다.
두 개의 비행기가 일렬로 만납니다.
동일 선상
주어진 그림에서 점 A, B, C는 동일 선상에 있습니다.

동시 라인
같은 지점에서 교차하는 세 개 이상의 선을 동시 선이라고합니다.
각도
공통 끝점 O를 갖는 두 광선 OA 및 OB는 각도 AOB를 형성하며 ∠AOB로 기록됩니다.

각도 측정
OA에서 OB로 전환하는 양을 m (∠AOB)로 쓰여진 ∠AOB의 마디라고합니다.
360 ° 각도
광선 OA가 원래 위치 OA에서 시작하여 시계 반대 방향으로 약 O 회전하고 완전한 회전이 원래 위치로 돌아온 후 360도 회전했다고합니다.이 완전한 회전은 360 ° 등분으로 나뉩니다. 그런 다음 각 부분을 1도라고하며 1 °로 표기합니다.
1 ° = 60 분, 60 '로 작성
1 분 = 60 초, 60 "로 작성
각도 유형
Right angle -측정 값이 90 ° 인 각도를 직각이라고합니다.
Acute angle -측정 값이 90 ° 미만인 각도를 예각이라고합니다.
Obtuse angle -측정 값이 90 ° 이상 180 ° 미만인 각도를 obtues 각도라고합니다.
Straight angle -측정 값이 180 ° 인 각도를 직선 각도라고합니다.
Reflex angle -측정 값이 180 ° 이상 360 ° 미만인 각도를 반사각이라고합니다.
Complete angle -측정 값이 360 ° 인 각도를 완전 각도라고합니다.
Equal angle -측정 값이 같으면 두 각도가 같다고합니다.
Complementary angle측정 값의 합이 90이면 두 각도는 보완 적이라고합니다. 예를 들어, 65 °와 25 °를 측정하는 각도는 보완 각도입니다.
Supplementary angle-측정 값의 합이 180 °이면 두 각도를 보완한다고합니다. 예를 들어 각도는 70 °이고 110 °는 보조입니다.
Adjacent angle-두 개의 각이 같은 정점과 하나의 공통 팔을 가지고 비 공통 팔이 코맨 팔의 양쪽에있는 경우 인접 각이라고합니다. 주어진 그림에서 ∠AOC와 ∠BOC는 인접 각도입니다.

중요한 결과
광선이 선 위에 있으면 이렇게 형성된 두 인접 각도의 합이 180 °가됩니다. 주어진 그림에서 광선 CP는 선 AB 위에 있습니다.

∴ ∠ACD + ∠BCD = 180°.
선의 주어진 지점에서 선의 같은면에 형성된 모든 각도의 합은 180 °입니다. 주어진 그림에서 4 개의 각도는 AOB의 같은면에 형성됩니다.

∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.
점 주위의 모든 각도의 합은 360 °입니다. 주어진 그림에서 점 O를 중심으로 5 개의 각도가 형성됩니다.

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
수직 반대 각도
두 개의 선 A Band CD가 점 O에서 교차하는 경우 AOC, BOD 및 BOC, AOD는 두 쌍의 수직 반대 각도입니다. 수직 반대 각도는 항상 동일합니다.
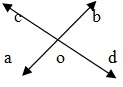
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
평행선
두 개의 선이 같은 평면에 있고 양쪽에서 생성 될 때 교차하지 않는 경우 이러한 선은 평행이라고 말하고 L || m이라고 씁니다.
평행선을 절단하는 횡단 선

두 개의 평행선 AB와 CD를 횡단 EF로 절단합니다. 그때
해당 각도는 동일합니다.
(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)대체 내부 각도는 동일합니다.
(∠3 =∠5 ) and (∠4 =∠6 )봉헌 내부 각도는 보완 적입니다.
∠4+∠5 = 180° and ∠3 +∠6 = 180°.삼각형
세 개의 직선으로 둘러싸인 도형을 삼각형이라고합니다. 주어진 그림에서 우리는 ∆ABC; ∆ABC는 세 개의 꼭지점 A, B, C를 가지고 있습니다. In에는 ∠A, ∠B 및 ∠C의 세 가지 각도가 있습니다. 그것은 AB, AC 및 BC의 세면을 가지고 있습니다.

삼각형의 종류
모든 변이 같은 삼각형을 정삼각형이라고합니다.
두 변이 같은 삼각형을 이등변 삼각형이라고합니다.
길이가 다른 모든 변을 가진 삼각형을 스켈 렌 삼각형이라고합니다.
각도가 90 ° 인 삼각형을 직각 삼각형이라고합니다.
각도가 90 °에서 180 ° 사이 인 삼각형을 둔각 삼각형이라고합니다.
각이 예각 인 삼각형을 예각 삼각형이라고합니다.
삼각형의 모든 변의 합을 삼각형의 둘레라고합니다.
삼각형의 두 변의 합이 세 번째 변보다 큽니다.
∠B = 90 ° 인 직각 ABC에서는 AC 2 = AB 2 + BC 2 입니다. 이것을 피타고라스 정리라고합니다.
사변형
4 개의 직선으로 둘러싸인 도형을 사변형이라고합니다. 사변형의 모든 각도의 합은 360 °입니다.
Rectangle-사각형은 반대쪽이 같고 각 각도가 90 ° 인 경우 사각형이라고합니다. 주어진 그림에서. ABCD는 직사각형입니다.

Square-사각형은 모든 변이 같고 각 각도가 90 ° 인 경우 사각형이라고합니다. 주어진 그림에서. ABCD는 AB = BC = CD = DA 인 정사각형입니다.

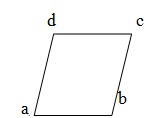
Parallelogram-사변형을 평행 사변형이라고합니다. 주어진 그림에서. ABCD는 AB = DC & AD = BC 인 평행 사변형입니다.

Rhombus-모든 변이 같은 평행 사변형을 마름모라고합니다. 주어진 그림에서. ABCD는 AB = BC = CD = DA, AB || DC와 AD || 기원전.
중요한 사실
사변형은 반대쪽이 같고 대각선이 같은 경우 직사각형입니다.
사변형은 모든 변이 같고 대각선이 같으면 정사각형입니다.
사변형은 평행 사변형입니다.
사변형은 평행 사변형이지만 직사각형은 아닙니다. 반대편은 같지만 대각선은 같지 않습니다.
사변형은 마름모이지만 모든 변이 같고 대각선이 같지 않으면 정사각형이 아닙니다.
사변형 결과
평행 사변형에서 우리는
반대편은 동일합니다.
반대 각도는 동일합니다.
각 대각선은 평행 사변형을 양분합니다.
평행 사변형의 대각선은 서로 이등분합니다.
직사각형의 대각선은 같습니다.
마름모의 대각선은 서로 직각으로 이등분합니다.
서클 결과

중심에서 코드까지 수직은 코드를 양분합니다.
동일 선상에 있지 않은 세 점을 통과하는 원은 하나뿐입니다.
반원의 각도는 직각입니다.
순환 사변형의 반대 각도는 보완 적입니다.
원의 같은 세그먼트에있는 각도는 같습니다.
원의 모든 지점에서 접선은 접점을 통해 반경에 수직입니다.
외부 점에서 원에 접하는 두 개는 동일합니다.
PT가 원에 접하고 PAB가 시컨트이면 PA x PB = PT 2