수렴 영역 (ROC)
라플라스 변환이 수렴하는 σ의 범위 변화를 수렴 영역이라고합니다.
라플라스 변환의 ROC 속성
ROC에는 s 평면에서 jω 축에 평행 한 스트립 선이 포함됩니다.

x (t)가 절대 적분이고 유한 기간이면 ROC는 전체 s- 평면입니다.
x (t)가 우변 수열이면 ROC : Re {s}> σ o .
x (t)가 좌변 시퀀스이면 ROC : Re {s} <σ o .
x (t)가 양면 시퀀스 인 경우 ROC는 두 영역의 조합입니다.
ROC는 아래의 예를 사용하여 설명 할 수 있습니다.
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$ LT [x (t)] = LT [e-^ {at} u (t)] = {1 \ over S + a} $
$ Re {} \ gt -a $
$ ROC : Re {s} \ gt> -a $

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {at} u (t)] = {1 \ over Sa} $
$ Re {s} <a $
$ ROC : Re {s} <a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {-at} u (t) + e ^ {at} u (-t)] = {1 \ over S + a} + {1 \ over Sa} $
$ {1 \ over S + a} Re \ {s \} \ gt -a $
$ {1 \ over Sa} Re \ {s \} \ lt a $

위의 다이어그램을 참조하면 조합 영역은 –a에서 a까지입니다. 그 후,
$ ROC : -a <Re {s} <a $
인과 관계 및 안정성
시스템이 인과 관계가 되려면 전달 함수의 모든 극이 s 평면의 오른쪽 절반이어야합니다.

전달 함수의 모든 극이 s- 평면의 왼쪽 절반에 놓일 때 시스템이 안정적이라고합니다.

전달 함수의 극 중 하나 이상이 s 평면의 오른쪽 절반으로 이동하면 시스템이 불안정하다고합니다.
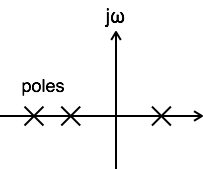
시스템은 전달 함수의 극 중 하나 이상이 s- 평면의 jω 축에있을 때 약간 안정적이라고합니다.

기본 기능의 ROC
| f (t) | F (s) | 큰 괴조 |
|---|---|---|
| $ u (t) $ | $$ {1 \ 초 이상} $$ | ROC : Re {s}> 0 |
| $ t \, u (t) $ | $$ {1 \ s ^ 2} $$ | ROC : Re {s}> 0 |
| $ t ^ n \, u (t) $ | $$ {n! \ over s ^ {n + 1}} $$ | ROC : Re {s}> 0 |
| $ e ^ {at} \, u (t) $ | $$ {1 \ over sa} $$ | ROC : Re {s}> a |
| $ e ^ {-at} \, u (t) $ | $$ {1 \ s + a 이상} $$ | ROC : Re {s}> -a |
| $ e ^ {at} \, u (t) $ | $$-{1 \ over sa} $$ | ROC : Re {s} <a |
| $ e ^ {-at} \, u (-t) $ | $$-{1 \ s + a 이상} $$ | ROC : Re {s} <-a |
| $ t \, e ^ {at} \, u (t) $ | $$ {1 \ 이상 (sa) ^ 2} $$ | ROC : Re {s}> a |
| $ t ^ {n} e ^ {at} \, u (t) $ | $$ {n! \ over (sa) ^ {n + 1}} $$ | ROC : Re {s}> a |
| $ t \, e ^ {-at} \, u (t) $ | $$ {1 \ 이상 (s + a) ^ 2} $$ | ROC : Re {s}> -a |
| $ t ^ n \, e ^ {-at} \, u (t) $ | $$ {n! \ over (s + a) ^ {n + 1}} $$ | ROC : Re {s}> -a |
| $ t \, e ^ {at} \, u (-t) $ | $$-{1 \ 이상 (sa) ^ 2} $$ | ROC : Re {s} <a |
| $ t ^ n \, e ^ {at} \, u (-t) $ | $$-{n! \ over (sa) ^ {n + 1}} $$ | ROC : Re {s} <a |
| $ t \, e ^ {-at} \, u (-t) $ | $$-{1 \ 이상 (s + a) ^ 2} $$ | ROC : Re {s} <-a |
| $ t ^ n \, e ^ {-at} \, u (-t) $ | $$-{n! \ over (s + a) ^ {n + 1}} $$ | ROC : Re {s} <-a |
| $ e ^ {-at} \ cos \, bt $ | $$ {s + a \ over (s + a) ^ 2 + b ^ 2} $$ | |
| $ e ^ {-at} \ sin \, bt $ | $$ {b \ over (s + a) ^ 2 + b ^ 2} $$ |