Z- 변환 속성
Z-Transform에는 다음과 같은 속성이 있습니다.
선형성 속성
만약 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
과 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
그런 다음 선형성 속성은
$a\, x (n) + b\, y (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} a\, X(Z) + b\, Y(Z)$
시간 이동 속성
만약 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
그런 다음 시간 이동 속성에 따르면
$x (n-m) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} z^{-m} X(Z)$
지수 시퀀스 속성에 의한 곱셈
만약 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
그런 다음 지수 시퀀스 속성을 곱하면 다음과 같이 나타납니다.
$a^n\, . x(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z/a)$
시간 반전 속성
만약 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
그런 다음 시간 반전 속성에 따르면
$x (-n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(1/Z)$
Z 도메인의 미분 또는 n 속성에 의한 곱셈
만약 $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
그런 다음 n으로 곱하거나 z 도메인 속성의 미분은 다음과 같이 말합니다.
$ n^k x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} [-1]^k z^k{d^k X(Z) \over dZ^K} $
Convolution 속성
만약 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
과 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
그런 다음 convolution 속성은 다음과 같이 말합니다.
$x(n) * y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z)$
상관 속성
만약 $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
과 $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
그런 다음 상관 속성에 따르면
$x(n) \otimes y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z^{-1})$
초기 값 및 최종 값 정리
인과 신호에 대해 z- 변환의 초기 값과 최종 값 정리가 정의됩니다.
초기 값 정리
인과 신호 x (n)의 경우 초기 값 정리는 다음과 같이 말합니다.
$ x (0) = \lim_{z \to \infty }X(z) $
이것은 역 z- 변환을 취하지 않고 신호의 초기 값을 찾는 데 사용됩니다.
최종 가치 정리
인과 신호 x (n)의 경우 최종 값 정리는 다음과 같이 말합니다.
$ x ( \infty ) = \lim_{z \to 1} [z-1] X(z) $
역 z 변환을 수행하지 않고 신호의 최종 값을 찾는 데 사용됩니다.
Z- 변환의 ROC (Region of Convergence)
z- 변환이 수렴하는 z의 변동 범위를 z- 변환 수렴 영역이라고합니다.
Z- 변환의 ROC 속성
z- 변환의 ROC는 z- 평면에서 원으로 표시됩니다.
ROC에는 극이 없습니다.
x (n)이 유한 기간 인과 시퀀스 또는 우변 시퀀스 인 경우 ROC는 z = 0을 제외한 전체 z 평면입니다.
x (n)이 유한 기간 반인과 시퀀스 또는 좌변 시퀀스 인 경우 ROC는 z = ∞를 제외한 전체 z 평면입니다.
x (n)이 무한 지속 인과 시퀀스 인 경우 ROC는 반경 aie | z |를 갖는 원의 외부입니다. > a.
x (n)이 무한 지속 시간 인과 적 시퀀스 인 경우 ROC는 반경 aie | z |를 갖는 원의 내부입니다. <a.
x (n)이 유한 기간 양측 시퀀스 인 경우 ROC는 z = 0 & z = ∞를 제외한 전체 z 평면입니다.
ROC의 개념은 다음 예제로 설명 할 수 있습니다.
Example 1: z 변환 및 ROC 찾기 $a^n u[n] + a^{-}nu[-n-1]$
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z \over Z-a} + {Z \over Z {-1 \over a}}$
$$ ROC: |z| \gt a \quad\quad ROC: |z| \lt {1 \over a} $$
ROC 플롯에는 a> 1 및 a <1의 두 가지 조건이 있습니다.

이 경우 ROC 조합이 없습니다.
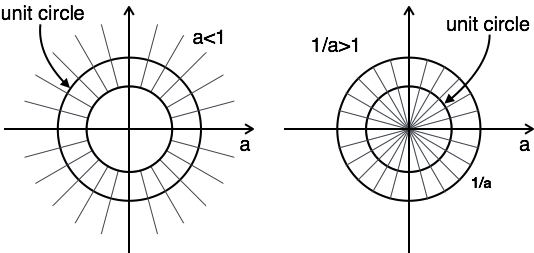
여기서 ROC의 조합은 $a \lt |z| \lt {1 \over a}$
따라서이 문제의 경우 a <1 일 때 z 변환이 가능합니다.
인과 관계 및 안정성
불연속 시간 LTI 시스템의 인과 관계 조건은 다음과 같습니다.
불연속 시간 LTI 시스템은
ROC는 가장 바깥 쪽 극 밖에 있습니다.
전달 함수 H [Z]에서 분자의 순서는 분모의 순서보다 클 수 없습니다.
Discrete Time LTI 시스템의 안정성 조건
이산 시간 LTI 시스템은 다음과 같은 경우 안정적입니다.
시스템 함수 H [Z]에는 단위 원 | z | = 1이 포함됩니다.
전달 함수의 모든 극은 단위 원 | z | = 1 안에 있습니다.
기본 신호의 Z 변환
| x (t) | X [Z] |
|---|---|
| $\delta$ | 1 |
| $u(n)$ | ${Z\over Z-1}$ |
| $u(-n-1)$ | $ -{Z\over Z-1}$ |
| $\delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z \over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z \over Z-a}$ |
| $n\,a^n u[n]$ | ${aZ \over |Z-a|^2}$ |
| $n\,a^n u[-n-1] $ | $- {aZ \over |Z-a|^2}$ |
| $a^n \cos \omega n u[n] $ | ${Z^2-aZ \cos \omega \over Z^2-2aZ \cos \omega +a^2}$ |
| $a^n \sin \omega n u[n] $ | $ {aZ \sin \omega \over Z^2 -2aZ \cos \omega +a^2 } $ |