Ułamkowa część koła
Pełne lub całe koło przyjmuje się jako 1, a części kół są reprezentowane jako ułamki. Na przykład, jeśli okrąg jest podzielony na 8 równych części, każda z części reprezentuje ułamek 1/8. Trzy części takiego koła reprezentowałyby 3/8 i dalej.
Tutaj mamy do czynienia z rodzajem problemów, w których podane są ułamki reprezentujące określone części koła i musimy znaleźć ułamek reprezentujący pozostałą nieznaną część koła. Aby rozwiązać takie problemy, sumujemy ułamki reprezentujące części ułamkowe, a następnie odejmujemy sumę od 1, czyli całego koła. Wynik daje ułamek reprezentujący nieznaną ułamkową część koła.
Jaka część koła jest niezacieniowana? Zapisz swoją odpowiedź jako ułamek w najprostszej formie.
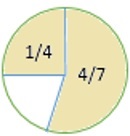
Rozwiązanie
Step 1:
Najpierw stwierdzamy, jaka część figury jest zacieniona.
$ \ frac {1} {4} $ + $ \ frac {4} {7} $ = $ \ frac {7} {28} $ + $ \ frac {16} {28} $ = $ \ frac {(7 +16)} {28} $ = $ \ frac {23} {28} $
Step 2:
Aby znaleźć niezacieniowany ułamek liczby, odejmujemy otrzymany wynik ( $ \ frac {23} {28} $ ) od 1.
1 - $ \ frac {23} {28} $ = $ \ frac {28} {28} $ - $ \ frac {23} {28} $ = $ \ frac {(28–23} {28} $ = $ \ frac {5} {28} $
Tak więc niezacieniona część liczby to $ \ frac {5} {28} $ .
Jaka część koła jest zacieniona? Zapisz swoją odpowiedź jako ułamek w najprostszej formie.
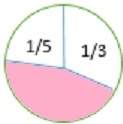
Rozwiązanie
Step 1:
Najpierw ustalamy, jaka część figury jest niezacieniowana.
$ \ frac {1} {5} $ + $ \ frac {1} {3} $ = $ \ frac {3} {15} $ + $ \ frac {5} {15} $ = $ \ frac {(3 +5)} {15} $ = $ \ frac {8} {15} $
Step 2:
Aby znaleźć niezacieniony ułamek liczby, odejmujemy otrzymany wynik ( $ \ frac {8} {15} $ ) od 1.
1 - $ \ frac {8} {15} $ = $ \ frac {15} {15} $ - $ \ frac {8} {15} $ = $ \ frac {(15–8)} {15} $ = $ \ frac {7} {15} $
Zatem ułamek liczby, który jest zacieniowany to $ \ frac {7} {15} $ .