Bokeh - wyspecjalizowane krzywe

Plik bokeh.plotting API obsługuje metody renderowania po wyspecjalizowanych krzywych -

beizer ()

Ta metoda dodaje krzywą Béziera do obiektu figury. Krzywa Béziera to krzywa parametryczna używana w grafice komputerowej. Inne zastosowania obejmują projektowanie czcionek komputerowych i animacji, projektowanie interfejsu użytkownika i wygładzanie trajektorii kursora.

W grafice wektorowej krzywe Béziera są używane do modelowania gładkich krzywych, które można skalować w nieskończoność. „Ścieżka” to połączenie połączonych krzywych Béziera.

Metoda beizer () ma następujące parametry, które są zdefiniowane -

1	x0	Współrzędne x punktów początkowych.
2	y0	Współrzędne y punktów początkowych.
3	x1	Współrzędne x punktów końcowych.
4	y1	Współrzędne y punktów końcowych.
5	cx0	Współrzędne x pierwszych punktów kontrolnych.
6	cy0	Współrzędne y pierwszych punktów kontrolnych.
7	cx1	Współrzędne x drugich punktów kontrolnych.
8	cy1	Współrzędne y drugich punktów kontrolnych.

Wartość domyślna dla wszystkich parametrów to Brak.

Przykład

Poniższy kod generuje stronę HTML pokazującą krzywą Béziera i parabolę na wykresie Bokeh -

x = 2
y = 4
xp02 = x+0.4
xp01 = x+0.1
xm01 = x-0.1
yp01 = y+0.2
ym01 = y-0.2
fig = figure(plot_width = 300, plot_height = 300)
fig.bezier(x0 = x, y0 = y, x1 = xp02, y1 = y, cx0 = xp01, cy0 = yp01,
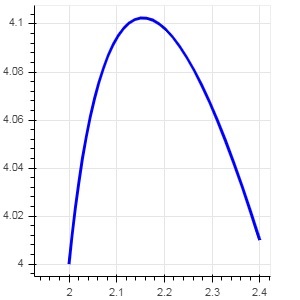
cx1 = xm01, cy1 = ym01, line_color = "red", line_width = 2)

Wynik

kwadratowy()

Ta metoda dodaje plik parabola glyphdo figury bokeh. Funkcja ma takie same parametry jak beizer (), z wyjątkiemcx0 i cx1.

Przykład

Kod podany poniżej generuje krzywą kwadratową.

x = 2
y = 4
xp02 = x + 0.3
xp01 = x + 0.2
xm01 = x - 0.4
yp01 = y + 0.1
ym01 = y - 0.2
x = x,
y = y,
xp02 = x + 0.4,
xp01 = x + 0.1,
yp01 = y + 0.2,
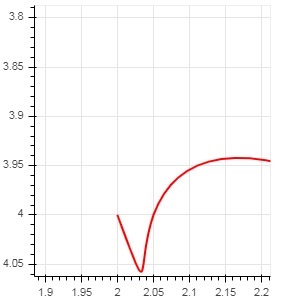
fig.quadratic(x0 = x, y0 = y, x1 = x + 0.4, y1 = y + 0.01, cx = x + 0.1,
cy = y + 0.2, line_color = "blue", line_width = 3)

Wynik