Obwody arytmetyczne
W poprzednim rozdziale omówiliśmy podstawowe zastosowania wzmacniacza operacyjnego. Zauważ, że podlegają one liniowym operacjom wzmacniacza operacyjnego. W tym rozdziale omówimy obwody arytmetyczne, które są również liniowymi zastosowaniami wzmacniacza operacyjnego.
Obwody elektroniczne, które wykonują operacje arytmetyczne, nazywane są jako arithmetic circuits. Korzystając ze wzmacniaczy operacyjnych, można zbudować podstawowe obwody arytmetyczne, takie jakadder i a subtractor. W tym rozdziale szczegółowo poznasz każdą z nich.
Sumator
Sumator to obwód elektroniczny, który generuje wyjście, które jest równe sumie zastosowanych wejść. W tej sekcji omówiono obwód sumatora oparty na wzmacniaczu operacyjnym.
Sumator oparty na wzmacniaczu operacyjnym wytwarza sygnał wyjściowy równy sumie napięć wejściowych przyłożonych do jego zacisku odwracającego. Jest również nazywany jakosumming amplifier, ponieważ wyjście jest wzmocnione.
Plik circuit diagram dodatku opartego na wzmacniaczu operacyjnym pokazano na poniższym rysunku -
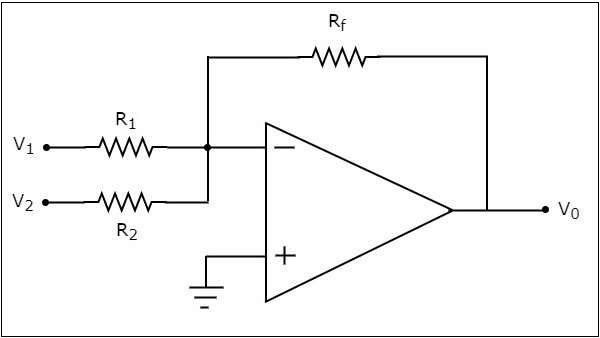
W powyższym obwodzie nieodwracający zacisk wejściowy wzmacniacza operacyjnego jest podłączony do masy. Oznacza to, że na jego nieodwracającym zacisku wejściowym podawane jest zero woltów.
Według virtual short concept, napięcie na odwracającym zacisku wejściowym wzmacniacza operacyjnego jest takie samo, jak napięcie na jego nieodwracającym zacisku wejściowym. Zatem napięcie na odwracającym zacisku wejściowym wzmacniacza operacyjnego będzie wynosić zero woltów.
Plik nodal equation w węźle odwracającego terminala wejściowego jest
$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {R_f} = 0 $$
$$ => \ frac {V_1} {R_1} - \ frac {V_2} {R_2} = \ frac {V_0} {R_f} $$
$$ => V_ {0} = R_ {f} \ left (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ right) $$
Jeśli $ R_ {f} = R_ {1} = R_ {2} = R $, to napięcie wyjściowe $ V_ {0} $ będzie wynosić -
$$ V_ {0} = - R {} \ left (\ frac {V_1} {R} + \ frac {V_2} {R} \ right) $$
$$ => V_ {0} = - (V_ {1} + V_ {2}) $$
Dlatego obwód sumatora oparty na wzmacniaczu operacyjnym omówiony powyżej da sumę dwóch napięć wejściowych $ v_ {1} $ i $ v_ {1} $, jako wyjście, gdy wszystkie rezystory obecne w obwodzie mają tę samą wartość . Zauważ, że napięcie wyjściowe $ V_ {0} $ obwodu sumatora manegative sign, co oznacza, że istnieje różnica faz 180 0 między wejściem a wyjściem.
Odejmowanie
Odejmowanie to obwód elektroniczny, który wytwarza wyjście, które jest równe różnicy zastosowanych wejść. W tej sekcji omówiono obwód odejmowania oparty na wzmacniaczu operacyjnym.
Odejmowanie oparte na wzmacniaczu operacyjnym wytwarza sygnał wyjściowy równy różnicy napięć wejściowych przyłożonych na jego zaciskach odwracających i nieodwracających. Jest również nazywany jakodifference amplifier, ponieważ wyjście jest wzmocnione.
Plik circuit diagram odejmowania opartego na wzmacniaczu operacyjnym pokazano na poniższym rysunku -
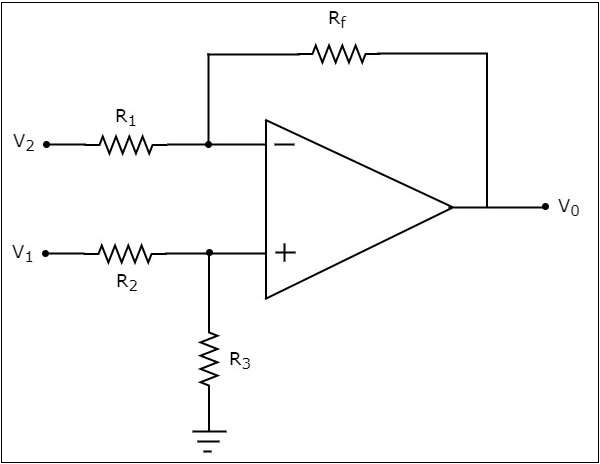
Teraz znajdźmy wyrażenie na napięcie wyjściowe $ V_ {0} $ powyższego obwodu za pomocą superposition theorem wykonując następujące kroki -
Krok 1
Po pierwsze, obliczyć napięcie wyjściowe $ V_ {01} $, biorąc pod uwagę tylko $ V_ {1} $.
W tym celu wyeliminuj $ V_ {2} $, powodując zwarcie. Następnie otrzymujemy plikmodified circuit diagram jak pokazano na poniższym rysunku -

Teraz używając voltage division principleobliczyć napięcie na nieodwracającym zacisku wejściowym wzmacniacza operacyjnego.
$$ => V_ {p} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) $$
Teraz powyższy obwód wygląda jak nieodwracający wzmacniacz o napięciu wejściowym $ V_ {p} $. Dlatego napięcie wyjściowe $ V_ {01} $ powyższego obwodu będzie wynosić
$$ V_ {01} = V_ {p} \ left (1+ \ frac {R_f} {R_1} \ right) $$
Zastępując, wartość $ V_ {p} $ w powyższym równaniu, otrzymujemy napięcie wyjściowe $ V_ {01} $ biorąc pod uwagę tylko $ V_ {1} $, as -
$$ V_ {01} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) $$
Krok 2
W tym kroku znajdźmy napięcie wyjściowe, $ V_ {02} $, biorąc pod uwagę tylko $ V_ {2} $. Podobnie jak w powyższym kroku, wyeliminuj $ V_ {1} $, powodując zwarcie. Plikmodified circuit diagram pokazano na poniższym rysunku.

Można zauważyć, że napięcie na nieodwracającym zacisku wejściowym wzmacniacza operacyjnego będzie wynosić zero woltów. Oznacza to, że powyższy obwód jest po prostu plikieminverting op-amp. Dlatego napięcie wyjściowe $ V_ {02} $ powyższego obwodu będzie wynosić -
$$ V_ {02} = \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
Krok 3
W tym kroku uzyskamy napięcie wyjściowe $ V_ {0} $ obwodu odejmującego o adding the output voltagesuzyskane w Kroku 1 i Kroku 2. Matematycznie można to zapisać jako
$$ V_ {0} = V_ {01} + V_ {02} $$
Zastępując w powyższym równaniu wartości $ V_ {01} $ i $ V_ {02} $, otrzymujemy -
$$ V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) + \ left (- \ frac {R_f} {R_1} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) - \ left (\ frac {R_f} {R_1} \ right) V_ {2} $$
Jeśli $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $, to napięcie wyjściowe $ V_ {0} $ będzie
$$ V_ {0} = V_ {1} \ left (\ frac {R} {R + R} \ right) \ left (1+ \ frac {R} {R} \ right) - \ left (\ frac { R} {R} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ left (\ frac {R} {2R} \ right) (2) - (1) V_ {2} $$
$$ V_ {0} = V_ {1} -V_ {2} $$
Zatem omawiany powyżej obwód odejmujący oparty na wzmacniaczu operacyjnym będzie generował wyjście, które jest różnicą dwóch napięć wejściowych $ V_ {1} $ i $ V_ {2} $, gdy wszystkie rezystory obecne w obwodzie mają tę samą wartość .