Przetworniki cyfrowo-analogowe
ZA Digital to Analog Converter (DAC)konwertuje cyfrowy sygnał wejściowy na analogowy sygnał wyjściowy. Sygnał cyfrowy jest reprezentowany za pomocą kodu binarnego, będącego kombinacją bitów 0 i 1. W tym rozdziale szczegółowo omówiono konwertery cyfrowo-analogowe.
Plik block diagram DAC pokazano na poniższym rysunku -
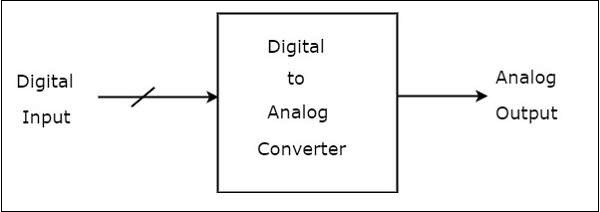
Przetwornik cyfrowo-analogowy (DAC) składa się z wielu wejść binarnych i jednego wyjścia. Ogólnie rzecz biorąc, pliknumber of binary inputs DAC będzie potęgą dwójki.
Rodzaje przetworników cyfrowo-analogowych
Tam są two types przetworników cyfrowo-analogowych
- DAC z rezystorem ważonym
- DAC drabinkowy R-2R
W tej sekcji szczegółowo omówiono te dwa typy przetworników cyfrowo-analogowych -
DAC z rezystorem ważonym
Przetwornik DAC z rezystorem ważonym wytwarza wyjście analogowe, które jest prawie równe wejściu cyfrowemu (binarnemu) przy użyciu binary weighted resistorsw odwracającym obwodzie sumatora. Krótko mówiąc, binarny DAC z rezystorem ważonym jest nazywany DAC z rezystorem ważonym.
Plik circuit diagram 3-bitowego binarnego DAC z rezystorem ważonym pokazano na poniższym rysunku -

Przypomnij sobie, że bity liczby binarnej mogą mieć tylko jedną z dwóch wartości. tj. 0 lub 1. Niech3-bit binary inputto $ b_ {2} b_ {1} b_ {0} $. Tutaj bity $ b_ {2} $ i $ b_ {0} $ oznaczająMost Significant Bit (MSB) and Least Significant Bit (LSB) odpowiednio.
Plik digital switchespokazane na powyższym rysunku zostaną połączone z masą, gdy odpowiednie bity wejściowe będą równe „0”. Podobnie przełączniki cyfrowe pokazane na powyższym rysunku zostaną podłączone do ujemnego napięcia odniesienia $ -V_ {R} $, gdy odpowiednie bity wejściowe są równe „1”.
W powyższym obwodzie nieodwracający zacisk wejściowy wzmacniacza operacyjnego jest podłączony do masy. Oznacza to, że do nieodwracającego zacisku wejściowego wzmacniacza operacyjnego podawane jest zero woltów.
Według virtual short concept, napięcie na odwracającym zacisku wejściowym wzmacniacza operacyjnego jest takie samo jak napięcie obecne na jego nieodwracającym zacisku wejściowym. Zatem napięcie w węźle odwracającego terminala wejściowego będzie wynosić zero woltów.
Plik nodal equation w węźle odwracającego terminala wejściowego jest:
$$ \ frac {0 + V_ {R} b_ {2}} {2 ^ {0} R} + \ frac {0 + V_ {R} b_ {1}} {2 ^ {1} R} + \ frac {0 + V_ {R} b_ {0}} {2 ^ {2} R} + \ frac {0-V_ {0}} {R_ {f}} = 0 $$
$$ => \ frac {V_ {0}} {R_ {f}} = \ frac {V_ {R} b_ {2}} {2 ^ {0} R} + \ frac {V_ {R} b_ {1 }} {2 ^ {1} R} + \ frac {V_ {R} b_ {0}} {2 ^ {2} R} $$
$$ => V_ {0} = \ frac {V_ {R} R_ {f}} {R} \ left \ {\ frac {b_ {2}} {2 ^ {0}} + \ frac {b_ {1 }} {2 ^ {1}} + \ frac {b_ {0}} {2 ^ {2}} \ right \} $$
Podstawiając, $ R = 2R_ {f} $ w powyższym równaniu.
$$ => V_ {0} = \ frac {V_ {R} R_ {f}} {2R_ {f}} \ left \ {\ frac {b_ {2}} {2 ^ {0}} + \ frac { b_ {1}} {2 ^ {1}} + \ frac {b_ {0}} {2 ^ {2}} \ right \} $$
$$ => V_ {0} = \ frac {V_ {R}} {2} \ left \ {\ frac {b_ {2}} {2 ^ {0}} + \ frac {b_ {1}} {2 ^ {1}} + \ frac {b_ {0}} {2 ^ {2}} \ right \} $$
Powyższe równanie reprezentuje output voltage equation3-bitowego DAC z rezystorem binarnym ważonym. Ponieważ liczba bitów na wejściu binarnym (cyfrowym) wynosi trzy, otrzymamy siedem możliwych wartości napięcia wyjściowego, zmieniając wejście binarne od 000 do 111 dla stałego napięcia odniesienia, $ V_ {R} $.
Możemy napisać generalized output voltage equation N-bitowego binarnego DAC z rezystorem ważonym, jak pokazano poniżej w oparciu o równanie napięcia wyjściowego 3-bitowego binarnego ważonego DAC z rezystorem.
$$ => V_ {0} = \ frac {V_ {R}} {2} \ left \ {\ frac {b_ {N-1}} {2 ^ {0}} + \ frac {b_ {N-2 }} {2 ^ {1}} + .... + \ frac {b_ {0}} {2 ^ {N-1}} \ right \} $$
Plik disadvantages binarnego ważonego rezystora DAC są następujące -
Różnica między wartościami rezystancji odpowiadającymi LSB i MSB będzie wzrastać wraz ze wzrostem liczby bitów obecnych na wejściu cyfrowym.
Trudno jest zaprojektować dokładniejsze rezystory, ponieważ liczba bitów obecnych na wejściu cyfrowym rośnie.
DAC drabinkowy R-2R
R-2R Ladder DAC przezwycięża wady binarnego DAC z rezystorem ważonym. Jak sama nazwa wskazuje, przetwornik DAC R-2R Ladder wytwarza wyjście analogowe, które jest prawie równe wejściu cyfrowemu (binarnemu) za pomocąR-2R ladder network w odwracającym obwodzie sumatora.
Plikcircuit diagram3-bitowego przetwornika cyfrowo-analogowego R-2R Ladder pokazano na poniższym rysunku -
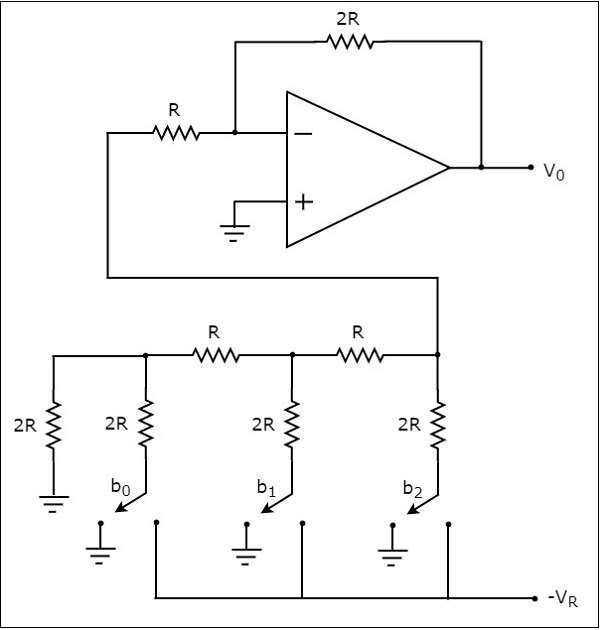
Przypomnij sobie, że bity liczby binarnej mogą mieć tylko jedną z dwóch wartości. tj. 0 lub 1. Niech3-bit binary inputto $ b_ {2} b_ {1} b_ {0} $. Tutaj bity $ b_ {2} $ i $ b_ {0} $ oznaczają odpowiednio najbardziej znaczący bit (MSB) i najmniej znaczący bit (LSB).
Przełączniki cyfrowe pokazane na powyższym rysunku zostaną podłączone do masy, gdy odpowiadające im bity wejściowe będą równe „0”. Podobnie przełączniki cyfrowe pokazane na powyższym rysunku zostaną podłączone do ujemnego napięcia odniesienia, $ -V_ {R} $, gdy odpowiadające im bity wejściowe są równe „1”.
Trudno jest uzyskać uogólnione równanie napięcia wyjściowego DAC-a drabinkowego R-2R. Ale możemy łatwo znaleźć analogowe wartości napięcia wyjściowego R-2R Ladder DAC dla indywidualnych kombinacji wejść binarnych.
Plik advantages DAC R-2R Ladder są następujące -
R-2R Ladder DAC zawiera tylko dwie wartości rezystora: R i 2R. Dlatego łatwo jest wybrać i zaprojektować dokładniejsze rezystory.
Jeżeli na wejściu cyfrowym jest więcej bitów, to musimy dodatkowo uwzględnić wymaganą liczbę sekcji R-2R.
Ze względu na powyższe zalety, przetwornik cyfrowo-analogowy R-2R Ladder jest korzystniejszy niż binarny przetwornik cyfrowo-analogowy z rezystorem ważonym.