Wzmacniacze Log And Anti Log
Obwody elektroniczne, które wykonują operacje matematyczne, takie jak logarytm i antylogarytm (wykładniczy) ze wzmocnieniem, nazywane są Logarithmic amplifier i Anti-Logarithmic amplifier odpowiednio.
W tym rozdziale omówiono platformę Logarithmic amplifier i Anti-Logarithmic amplifierszczegółowo. Należy pamiętać, że te wzmacniacze podlegają zastosowaniom nieliniowym.
Wzmacniacz logarytmiczny
ZA logarithmic amplifierlub a log amplifier, to układ elektroniczny, który generuje sygnał wyjściowy proporcjonalny do logarytmu zastosowanego wejścia. W tej sekcji szczegółowo omówiono wzmacniacz logarytmiczny oparty na wzmacniaczu operacyjnym.
Wzmacniacz logarytmiczny oparty na wzmacniaczu operacyjnym wytwarza na wyjściu napięcie, które jest proporcjonalne do logarytmu napięcia przyłożonego do rezystora podłączonego do jego zacisku odwracającego. Plikcircuit diagram na poniższym rysunku przedstawiono wzmacniacz logarytmiczny oparty na wzmacniaczu operacyjnym -
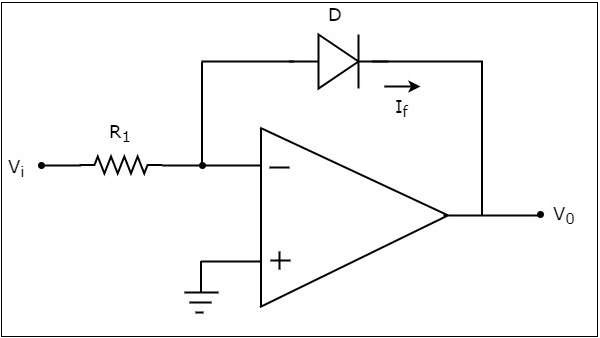
W powyższym obwodzie nieodwracający zacisk wejściowy wzmacniacza operacyjnego jest podłączony do masy. Oznacza to, że do nieodwracającego zacisku wejściowego wzmacniacza operacyjnego podawane jest zero woltów.
Według virtual short concept, napięcie na odwracającym zacisku wejściowym wzmacniacza operacyjnego będzie równe napięciu na jego nieodwracającym zacisku wejściowym. Zatem napięcie na odwracającym zacisku wejściowym będzie wynosić zero woltów.
Plik nodal equation w węźle odwracającego terminala wejściowego jest -
$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$
$$ => I_ {f} = \ frac {V_i} {R_1} ...... Równanie 1 $$
Poniżej znajduje się plik equation for current przepływa przez diodę, gdy jest przesunięta do przodu -
$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... Równanie 2 $$
gdzie,
$ I_ {s} $ to prąd nasycenia diody,
$ V_ {f} $ to spadek napięcia na diodzie, gdy jest przesunięta w przód,
$ V_ {T} $ jest termicznym równoważnikiem napięcia diody.
Plik KVL equation wokół pętli sprzężenia zwrotnego wzmacniacza operacyjnego będzie -
$$ 0-V_ {f} -V_ {0} = 0 $$
$$ => V_ {f} = - V_ {0} $$
Zastępując wartość $ V_ {f} $ w równaniu 2, otrzymujemy -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} ...... Równanie 3 $$
Zauważ, że wyrazy po lewej stronie zarówno równania 1, jak i równania 3 są takie same. Dlatego zrównaj prawostronny termin tych dwóch równań, jak pokazano poniżej -
$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
Stosowanie natural logarithm po obu stronach otrzymujemy -
$$ In \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$
$$ V_ {0} = - {nV_T} In \ left (\ frac {V_i} {R_1I_s} \ right) $$
Zauważ, że w powyższym równaniu parametry n, $ {V_T} $ i $ I_ {s} $ są stałymi. Zatem napięcie wyjściowe $ V_ {0} $ będzie proporcjonalne donatural logarithm napięcia wejściowego $ V_ {i} $ dla stałej wartości rezystancji $ R_ {1} $.
Dlatego obwód wzmacniacza logarytmicznego oparty na wzmacniaczu operacyjnym omówiony powyżej wytworzy wyjście, które jest proporcjonalne do logarytmu naturalnego napięcia wejściowego $ {V_T} $, gdy $ {R_1I_s} = 1V $.
Zauważ, że napięcie wyjściowe $ V_ {0} $ ma negative sign, co oznacza, że istnieje różnica faz 180 0 między wejściem a wyjściem.
Wzmacniacz antylogarytmiczny
Na anti-logarithmic amplifierlub anti-log amplifier, to układ elektroniczny, który generuje sygnał wyjściowy proporcjonalny do antylogarytmu zastosowanego wejścia. W tej sekcji szczegółowo omówiono wzmacniacz antylogarytmiczny oparty na wzmacniaczu operacyjnym.
Wzmacniacz antylogarytmiczny oparty na wzmacniaczu operacyjnym wytwarza na wyjściu napięcie, które jest proporcjonalne do antylogarytmu napięcia przykładanego do diody podłączonej do jej zacisku odwracającego.
Plik circuit diagram na poniższym rysunku przedstawiono wzmacniacz antylogarytmiczny oparty na wzmacniaczu operacyjnym -

W pokazanym powyżej obwodzie nieodwracający zacisk wejściowy wzmacniacza operacyjnego jest podłączony do masy. Oznacza to, że do nieodwracającego zacisku wejściowego podawane jest zero woltów.
Według virtual short concept, napięcie na odwracającym zacisku wejściowym wzmacniacza operacyjnego będzie równe napięciu obecnemu na jego nieodwracającym zacisku wejściowym. Zatem napięcie na jego odwracającym zacisku wejściowym będzie wynosić zero woltów.
Plik nodal equation w węźle odwracającego terminala wejściowego jest -
$$ - I_ {f} + \ frac {0-V_0} {R_f} = 0 $$
$$ => - \ frac {V_0} {R_f} = I_ {f} $$
$$ => V_ {0} = - R_ {f} I_ {f} ......... Równanie 4 $$
Wiemy, że równanie dla prądu przepływającego przez diodę, gdy jest odchylona do przodu, jest takie, jak podano poniżej -
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)} $$
Zastępując wartość $ I_ {f} $ w równaniu 4, otrzymujemy
$$ V_ {0} = - R_ {f} \ left \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} \ right \} $$
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} ...... Równanie 5 $$
Równanie KVL po stronie wejściowej zacisku odwracającego wzmacniacza operacyjnego będzie
$$ V_ {i} -V_ {f} = 0 $$
$$ V_ {f} = V_ {i} $$
Zastępując, wartość w równaniu 5, otrzymujemy -
$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ right)}} $$
Zauważ, że w powyższym równaniu parametry n, $ {V_T} $ i $ I_ {s} $ są stałymi. Zatem napięcie wyjściowe $ {V_0} $ będzie proporcjonalne doanti-natural logarithm (wykładniczy) napięcia wejściowego $ {V_i} $, dla stałej wartości rezystancji sprzężenia zwrotnego $ {R_f} $.
Dlatego obwód wzmacniacza antylogarytmicznego oparty na wzmacniaczu operacyjnym omówiony powyżej wytworzy wyjście, które jest proporcjonalne do logarytmu antynaturalnego (wykładniczego) napięcia wejściowego $ {V_i} $, gdy $ {R_fI_s} = 1V $. Zauważ, że napięcie wyjściowe $ {V_0} $ manegative sign, co oznacza, że istnieje różnica faz 180 0 między wejściem a wyjściem.